Pi Sayısı Nedir? π Sayısı Nasıl Hesaplanır ve Ne İşe Yarar?

Pi sayısı ( $π\pi$ ), 3.14159... diye başladıktan sonra, durmaksızın devam eden bir sayı ve matematiksel bir sabittir.^{[1], [27]} Öklidyen geometri çerçevesinde pi sayısı, bir çemberin çevresinin çapına oranı olarak tanımlanır; ancak pi sayısının bundan başka tanımları da mevcuttur. $π\pi$ (veya π) sembolüyle kullanımına ilk olarak İskoç matematikçi William Jones tarafından 1706'da rastlansa da, Antik Yunan filozofları tarafından keşfedildiği bilinmektedir ve hatta Arşimet Katsayısı olarak da bilinmektedir.^[2]

Günümüzde pi sayısı; matematik, fizik, mühendislik, mimari ve daha birçok yerde karşımıza çıkmaktadır; medeniyetimiz içerisinde vazgeçilmez bir role sahip olduğu rahatlıkla söylenebilir.

Pi sayısının, bir çemberin çevresinin çapına oranı olduğunu geometrik olarak gösteren bir animasyon. Buradaki çember, çapına bağlı olarak kendi çevresi etrafında döndükçe, çevresinin taradığı alan, çapının (1 birimin) pi katı olmaktadır.

Wikipedia

En temel tanımı dairenin geometrik özellikleri ile ilgili olduğu için $π\pi$ , trigonometri ve geometrideki birçok formülde, özellikle de daireler, elipsler ve kürelerle ilgili olan formüllerde karşımıza çıkar. Daha modern matematiksel analizdeyse pi sayısı, geometrik bağlamından bağımsız olarak, bir "özdeğer" veya bir "periyot" olarak tanımlanır. Bu nedenle pi sayısı, dairelerin geometrisi ile pek ilgisi olmayan sayı teorisi ve istatistik gibi matematik ve bilim alanlarında ve fiziğin/mühendisliğin neredeyse tüm alanlarında karşımıza çıkar.

$π\pi$ sayısı, böylesine geniş bir alanda karşımıza çıktığı için, hem bilim camiasında hem de popüler kültürde en yaygın bilinen matematiksel sabitlerden biridir. Bugüne kadar direkt olarak pi sayısıyla ilgili olan birden fazla kitap yayınlanmıştır ve pi sayısının basamaklarına yönelik hesaplama rekorlarının kırılması hâlen haber değeri taşıyan bir başarı olarak görülmektedir.

Matematik ile ilgili diğer içerikler ›

Ayrıca pi sayısının basamaklarının ezberlenmesi de matematikseverler arasında, pifiloloji olarak isimlendirilen eğlenceli bir hobi olarak görülmektedir:^[28] 2022 itibariyle rekor, pi sayısının noktadan sonra 70.030 basamağını 17 saat 14 dakika içinde ezbere ve doğru bir şekilde sayan Hindistanlı Suresh Kumar Sharma'ya aittir. Rekor, 21 Ekim 2015 tarihinden bu yana kırılamamıştır.

Pi Sayısının Özellikleri

Pi Sayısı, Sonsuz mu?

Her ne kadar pi sayısının tam değeri, yani nerede sona erdiği henüz bilinmese de ve sayının muhtemelen bir sonu olmasa da, semantik nedenlerle pi sayısının "sonsuza kadar devam ettiğini" söylemek yanıltıcı olabilir; çünkü matematikte sonsuzluk bir sayı değil, bir kavramdır.^{[3], [4]} Dolayısıyla pi sayısının "sonsuz" olduğunu veya "sonsuza kadar devam ettiğini" (İng: "infinite") söylemek yerine; sınırlarının belirsiz olduğunu (İng: "indefinite") söylemek daha doğrudur.^[5] Ancak çoğu zaman bu fark üzerinde yeterince durulmadığından, pi sayısının ondalık basamaklarının sonsuza kadar gittiği söylenebilmektedir. Bu, sadece pi sayısına özgü bir özellik değildir; bütün irrasyonel sayılar için geçerlidir.^[29]

Pi Sayısı, (Muhtemelen) Kendini Tekrar Etmez!

Ayrıca pi sayısının ondalıklı kısmında, kendini tekrar eden ve matematiksel olarak ifade edilebilecek bir örüntüye de henüz rastlanmamıştır.

Evrim Ağacı'ndan Mesaj

Neden Desteğe İhtiyacımız Var?

Aslında maddi destek istememizin nedeni çok basit: Çünkü Evrim Ağacı, bizim tek mesleğimiz, tek gelir kaynağımız. Birçoklarının aksine bizler, sosyal medyada gördüğünüz makale ve videolarımızı hobi olarak, mesleğimizden arta kalan zamanlarda yapmıyoruz. Dolayısıyla bu işi sürdürebilmek için gelir elde etmemiz gerekiyor. Bunda elbette ki hiçbir sakınca yok; kimin, ne şartlar altında yayın yapmayı seçtiği büyük oranda bir tercih meselesi. Ne var ki biz, eğer ana mesleklerimizi icra edecek olursak... Daha fazla göster

Bunda elbette ki hiçbir sakınca yok; kimin, ne şartlar altında yayın yapmayı seçtiği büyük oranda bir tercih meselesi. Ne var ki biz, eğer ana mesleklerimizi icra edecek olursak (yani kendi mesleğimiz doğrultusunda bir iş sahibi olursak) Evrim Ağacı'na zaman ayıramayacağımızı, ayakta tutamayacağımızı biliyoruz. Çünkü az sonra detaylarını vereceğimiz üzere, Evrim Ağacı sosyal medyada denk geldiğiniz makale ve videolardan çok daha büyük, kapsamlı ve aşırı zaman alan bir bilim platformu projesi. Bu nedenle bizler, meslek olarak Evrim Ağacı'nı seçtik.

Eğer hem Evrim Ağacı'ndan hayatımızı idame ettirecek, mesleklerimizi bırakmayı en azından kısmen meşrulaştıracak ve mantıklı kılacak kadar bir gelir kaynağı elde edemezsek, mecburen Evrim Ağacı'nı bırakıp, kendi mesleklerimize döneceğiz. Ama bunu istemiyoruz ve bu nedenle didiniyoruz.

Destek Ol

Buna bağlı olarak pi sayısının içinde, var olabilecek tüm sayıların sonlu kombinasyonlarının bulunabileceği düşünülmektedir. Ancak bu, ispatlanmış bir iddia değildir; sadece öyle gibi gözükmektedir.^[6] Çünkü (örneğin) 0.011000111100000111111... diye giden sayı da irrasyonel bir sayıdır ve basamakları tıpkı pi sayısı gibi sonsuza dek gider; ancak bariz bir şekilde, bünyesinde diğer tüm sayıları barındırmaz (ve barındıramaz da).^[7]

Pi Sayısı, İrrasyoneldir!

Daha matematiksel bir tanım yapmamız gerekirse, pi sayısının irrasyonel olduğunu söylemek daha doğru olacaktır. Yani pi sayısı, iki tam sayının bölümü olarak ( $mn\frac{m}{n}$ ) ifade edilemez. Bir diğer deyişle, ondalık basamaklarının sonunu tespit etmemiz mümkün değildir.

Sadece pi sayısı da değil: 2.71828... diye giden e sayısı, 1.618033... diye giden altın oran veya basitçe $2\sqrt{2}$ sayısı, irrasyoneldir. Hiçbir şekilde iki tam sayının birbirine oranı şeklinde ifade edilemezler.^{[8], [9]} Ancak pi sayısını sonsuz oranlar şeklinde tanımlamak mümkündür. Örneğin:

$π=3+17+115+11+1292+11+11+11+⋱\Large{\pi=3+\frac{1}{7+\frac{1}{15+\frac{1}{1+\frac{1}{292+\frac{1}{1+\frac{1}{1+\frac{1}{1+\ddots}}}}}}}}$

Hatta bu sonsuz kesirli sayılarda bazı örüntüler bile tespit edilebilmiştir. Örneğin, faydalı olabilecek bir diğer sonsuz kesir şudur:

$π=3+126+326+526+726+926+1126+1326+⋱\Large{\pi=3+\frac{1^2}{6+\frac{3^2}{6+\frac{5^2}{6+\frac{7^2}{6+\frac{9^2}{6+\frac{11^2}{6+\frac{13^2}{6+\ddots}}}}}}}}$

Pi Sayısı, 22/7 Değildir!

Belki lisede pi sayısının $22/7$ olarak ifade edilebileceğini öğrenmiş olabilirsiniz; ancak bu, $π\pi$ için pek iyi bir yakınsama değildir ve ondan %0.04 oranında uzak bir sayıdır (ayrıca 22/7, doğal olarak, rasyonel bir sayıdır ve bu nedenle irrasyonel olan pi sayısına eşit olamaz):

$22/7 = 3.14285714286$

$π=3.14159265358979323846264338327950288419716939...\pi=3.1415926535 8979323846 2643383279 5028841971 6939...$

Bu ufacık fark belirli uygulamalarda kabul edilebilir bulunabilir; ancak matematiksel olarak eşitlik iddia etmekte kullanılamaz. Bu konuya yazının ilerleyen kısımlarında döneceğiz.

Pi Sayısı, Transendentaldir!

Pi sayısını biraz daha özel kılan ise transendental sayı olmasıdır; yani rasyonel katsayılara sahip bir polinomun kökü (çözümü) olarak da ifade edilemez. Örneğin altın oran olarak bilinen ve 1.618033... diye giden sayı da irrasyonel bir sayıdır ve altın sayının basamaklarının sonu da bilinmemektedir; ancak bu sayı, bir transendentel sayı değildir; çünkü $x^2-x-1=0$ polinomunun köklerinden biridir.

Bunun birçok anlamından biri şudur: Pi sayısı; rasyonel sayıların veya köklerin sınırlı bir kombinasyonu olarak yazılamaz (örneğin pi sayısı, $313\sqrt[3]{31}$ veya $10\sqrt{10}$ olarak yazılamaz).

Pi Sayısı Ne İşe Yarar?

Başta da sözünü ettiğimiz gibi pi sayısı, bilimdeki en temel ve en önemli sabitlerden biridir. Burada, karşımıza çıktığı alanların bir kısmının fazlasıyla kısaltılmış bir özetini bulacaksınız.

Agora Bilim Pazarı

Organik Kimya Yapı ve İşlev

Boyut: 20 x 28
Sayfa Sayısı: 1426
Basım: 6
Basım Yeri: Ankara
ISBN No: 9786054414659

Devamını Göster

₺543.00

Satın Al Tüm Ürünler

Geometri

Pi sayısının en bariz kullanımı, "çember" veya "daire" olarak ifade ettiğimiz geometrik şekilleri tanımlamakta kullanılmasıdır. Pi sayısı, bir çemberin çevresinin çapına oranıdır:

$π=Cd\pi=\frac{C}{d}$

Bunun anlamı şudur: Bütün çemberlerin çevrelerinin çaplarına oranı, her zaman sabittir ve pi sayısına eşittir. Bir çemberin çapı 1 mikrometre de olsa, 1 ışık yılı genişliğinde de olsa, o çemberin çevresinin çapına oranı pi sayısına eşit olacaktır. Elbette bu, sadece düz (Öklidyen) geometri için geçerlidir; eğri (Öklidyen-olmayan) geometrilerde de benzer sabitler tanımlanabilir; fakat bunlar pi sayısına eşit olmayacaktır.

Ayrıca pi sayısı, bir dizi geometrik işlemde karşımıza çıkar:

Yarıçapı $r$ olan bir çemberin çevresi $2πr2\pi r$ 'dir.
Yarıçapı $r$ olan bir çemberin alanı $πr2\pi r^2$ 'dir.
Yarı-majör eksenlerinden biri $a$ , diğeri $b$ olan bir elipsin alanı $πab\pi ab$ 'dir.
Yarıçapı $r$ olan bir kürenin hacmi $43πr3\frac{4}{3}\pi r^3$ 'tür.
Yarıçapı $r$ olan bir kürenin yüzey alanı $4πr24\pi r^2$ 'dir.

Trigonometri

Trigonometrik fonksiyonlar, açılardan faydalanır ve açılar, genellikle radyan cinsinden ölçülür. Radyan olarak ölçülen açılarda pi sayısı büyük neme sahiptir; zira 1 tam çember $2π2\pi$ düzeyinde bir açıyı tarar.^[30] Dolayısıyla derece cinsinden açı hesabında $1°=π/1801\degree=\pi / 180$ olarak hesaplanır.

Ayrıca yaygın olarak kullanılan trigonometrik fonksiyonlar da pi sayısınınkatları olarak ifade edilebilirler. Örneğin $sin⁡\sin$ ve $cos⁡\cos$ fonksiyonları $2π2\pi$ 'lik bir periyoda sahiptir.

Pi Sayısının Tarihi ve Basamaklarını Bulma Yarışı

Pi sayısının bilinen bir sonu olmadığından ve sayı irrasyonel olduğundan, bu sayının basamaklarını doğru olarak tespit edebilecek bir algoritma/yöntem geliştirme çabası antik zamanlardan beri süregelmektedir. Burada, kronolojik bir sırada pi sayısının yolculuğuna kısa bir bakış atacağız. Burada kronolojik bir sıra veriyor olsak da, bahsedeceğimiz devirlerde birçok matematiksel atılımın, çok geniş coğrafyalara dağılmış halde ve birbirinden tamamen bağımsız/habersiz olarak yapıldığını hatırlatmakta fayda görüyoruz.

Pi sayısının en erken ne zaman isabetli bir şekilde hesaplandığına yönelik ilk iddia, Antik Mısır'a aittir: MÖ 2550-2490 yılları arasında inşa edilen Mısır Piramitleri'nin astronomik ve geometrik detayları üzerine yapılan (çoğu abartılı ve gerçek dışı olan) incelemelerden yola çıkan bazı Mısırologlar, Antik Mısırlılar'ın pi sayısını 22/7 olarak tespit ettikleri iddia etmişlerdir - ve bu konu, sonradan "Antik Mısır bilgeliğine" yönelik absürt (hatta yer yer "uzaylı müdahelelerini" içerecek kadar bilimdışı) iddialara konu olmuştur.^{[10], [11], [12]} Ancak iddia, modern matematikçiler ve tarihçiler yoğun eleştiriye maruz kalmıştır ve günümüzde kabul görmemektedir.^{[13], [14], [15], [16]}

Buna rağmen, pi sayısının yakınsamalarına yönelik ilk yazılı kaynaklar gerçekten de Babil ve Mısır metinlerinden gelmektedir (Mısır'dan kalma metinler, piramitlerin inşasından çok sonrasına denk gelmektedir). Örneğin Babiller'e ait MÖ 1900-1600 yıllarına tarihlenen bir kil tablet, pi sayısının 25/8=3.125 değerine sahip olduğunu ileri sürmektedir.^[16] MÖ 1650 yılına tarihlenen ve MÖ 1850 yılından kalma bir dokümanı kopyalayan Rhind Papirusu'nda pi sayısı $(169)2=3.16(\frac{16}{9})^2=3.16$ olarak alınmıştır.^[17]

MÖ 1200 yılında Çin'de pi sayısı 3 olarak hesaplanmıştır. Yunan filozof ve matematikçi Anaksagoras, MÖ 434 yılında sayıyı 3.088311.. olarak giden bir sayı olarak hesaplamıştır.

Hindistan'da MÖ 4. yüzyılda yazılan ve astronomik hesaplamaları içeren Shatapatha Brahmana metninde pi sayısı $339108≈3.139\frac{339}{108}\approx3.139$ olarak alınmıştır.^[18] MÖ 150 yılından kalma diğer Hint metinlerinde pi sayısı $10≈3.1622\sqrt{10}\approx3.1622$ olarak belirlenmiştir.^[17]

Nihayet Arşimet, MÖ 250 yılında $π\pi$ sayısını arzu ettiğiniz basamağa kadar bulabileceğiniz bir algoritma geliştirmiştir.^[19] Arşimet, döngüsel bir algoritma kullanarak pi sayısının $22371\frac{223}{71}$ ile $227\frac{22}{7}$ arasında olduğunu bulmuştur. Buna göre:

$3.1408<π<3.14293.1408<\pi<3.1429$

Muhtemelen daha önceden sözünü ettiğimiz $π=227\pi=\frac{22}{7}$ inancı da bu hesaplamadan köken almaktadır.

MS 100'lü yıllarda Çinli matematikçiler de Hintliler gibi $10\sqrt{10}$ sonucuna varmışlardır. MS 150 yılında Ptolemy, Almagest isimli eserinde pi sayısının 3.1416 olduğunu hesaplamıştır; ancak muhtemelen bu sayıyı kendisi hesaplamadı ve ya Arşimet'ten ya da Pergalı Apollonius'tan aldı.^{[17], [20]}

MS 3. yüzyılda Çinli matematikçiler pi sayısını $14245≈3.1556\frac{142}{45}\approx3.1556$ olarak hesaplamışlardır. 265 yılında Wei Krallığı'ndan matematikçi Liu Hui, poligon-temelli bir algoritma kullanarak pi sayısını $3.1416$ olarak hesaplamışlardır.^[20] 5. yüzyıldaysa, sonsuz serileri kullanarak pi sayısını 7. basamağına kadar tespit etmeyi başarmışlardır: 480 yılında Çinli matematikçi Zu Chongzhi, pi sayısı için şu aralığı belirlemiştir:

$3.1415926<π<3.14159273.1415926<\pi<3.1415927$

Bu aralığı veren yakınsama kesirleri olarak da $355113\frac{355}{113}$ ve $227\frac{22}{7}$ kesirlerini önermiştir. Bunlardan küçük olan kesire "Milü" (Tür: "yakın oran"), büyük olan kesire "Yeülü" (Tür: "yakınsak oran") adını vermiştir. Bu 7 basamaklı yakınsama, sonraki 800 yıl boyunca rekor olarak kalmıştır.

499 yılında Hintli matematikçi Aryabhata, pi sayısını 3.1416 olarak hesaplamıştır. 1220 yılındaysa Fibonacci, yine bir poligon metodu yardımıyla (Arşimet'ten bağımsız olarak) pi sayısını 3.1418 olarak hesaplamıştır. İtalyan yazar Dante, pi sayısı için $3+210≈3.141423+\frac{\sqrt{2}}{10}\approx3.14142$ yakınsamasını önermiştir.

1424 yılında Pers matematikçi Gıyaseddin Cemşid, pi sayısının 60'lık sistemde 9 basamağını (yani 10'luk sistem yaklaşık 16 basamağını) hesaplayarak, Çin'in rekorunu kırmayı başarmıştır. Bu rekor, 180 yıl boyunca tekrar kırılamamıştır.

1579 yılında Fransız matematikçi François Viète, pi sayısının 9 basamağını doğru olarak hesaplamayı başarmıştır.

1593 yılında Flaman matematikçi Adriaan van Roomen, rekoru 15 basamağa çıkarmıştır. Birazdan detaylarını anlatacağımız gibi, NASA'nın bugün kullandığı basamak sayısı bu kadardır.

1596 yılında Hollandalı matematikçi Ludolph van Ceulen, 20 basamağa ulaşmıştır; kısa bir süre sonra da 35 basamağa çıkarmıştır. Bu müthiş başarı nedeniyle $π\pi$ sayısı Almanya'da 20. yüzyıla kadar "Ludolph Sayısı" olarak anılmıştır.

Hollandalı matematikçi Willebrord Snellius, 1621 yılında 34 basamağa kadar hesaplama yapabilmiştir; 1630 yılındaysa Avusturyalı astronom Christoph Grienberger 38 basamağa ulaşmıştır.

Bu tür antik yöntemler, az sayıda basamağı tespit etmek istediğinizde avantajlıdır; ancak eğer ki amacınız pi sayısının 50 milyonuncu basamağını bulmaksa, bu tür yöntemler fazlasıyla yavaş ve zahmetli olacaktır. Gerçekten de poligon yakınsaması gibi antik yöntemlerle pi sayısının 39. basamağı anca 1630 yılında, 71. basamağı ise 1699 yılında hesaplanabilmiştir.^[17]

Bu sorunu çözmek için iki yöntem kullanabilirsiniz: kalkülüs ve bilgisayarlar.

Kalkülüsün İcadı ve Pi Sayısının Matematiksel Yakınsamaları

Isaac Newton ve Gottfried Wilhelm Leibniz'in birbirinden bağımsız olarak kalkülüsü icat etmeleri sonucunda, pi sayısının yüzlerce basmaağı hesaplanabilir hâle gelmiştir - ki az sonra göreceğimiz gibi bu, bilimsel işlemler için fazlasıyla yeterlidir.

Kalkülüsten yararlanan ilk yakınsama, 1593 yılında Fransız matematikçi François Viète tarafından geliştirilmiştir:

$2π=22⋅2+22⋅2+2+22…\frac{2}{\pi}=\frac{\sqrt{2}}{2}\cdot\frac{\sqrt{2+\sqrt{2}}}{2}\cdot\frac{\sqrt{2+\sqrt{2+\sqrt{2}}}}{2}\dots$

Görülebileceği gibi bu ilk yakınsamalar, sonradan gelenekselleşecek sonsuz toplamlar yerine, sonsuz çarpma yöntemini kullanmaktadır.

1655 yılında John Wallis, benzer bir yakınsama denemiştir:

$π2=(21⋅23)⋅(43⋅45)⋅(65⋅67)⋅(87⋅89)…\frac{\pi}{2}=(\frac{2}{1}\cdot\frac{2}{3})\cdot(\frac{4}{3}\cdot\frac{4}{5})\cdot(\frac{6}{5}\cdot\frac{6}{7})\cdot(\frac{8}{7}\cdot\frac{8}{9})\dots$

Bu iki yakınsamanın kalkülüsün icadından önce gelmesi takdire şayandır. Kalkülüs sonrası ilk yakınsama, İskoç matematikçi James Gregory tarafından 1671'de, sonrasındaysa birebir aynı yakınsama, 1674'te Leibniz tarafından yapılmıştır (bu nedenle buna Gregory-Leibniz Serisi denmektedir):

$arctan⁡z=z−z35+z55−z77+…\arctan{z}=z-\frac{z^3}{5}+\frac{z^5}{5}-\frac{z^7}{7}+\dots$

Bu seriyi $z = 1$ için hesapladığınızda, sonuç $π/4\pi/4$ olmaktadır.^[21]

Bu seri basit kalkülüs açısından faydalı olsa da, algoritmik olarak pi sayısına gereğinden yavaş yakınsayan bir yakınsamadır. Bu nedenle 1706 yılında John Machin, aynı seriyi geliştirerek çok daha hızlı bir yakınsama elde etmiştir:

$π4=4arctan⁡15−arctan⁡1239\frac{\pi}{4}=4\arctan\frac{1}{5}-\arctan\frac{1}{239}$

Machin, bu yakınsamayı kullanarak noktadan sonraki 100. basamağa kadar erişebilmiştir. Kendisinden sonra gelen matematikçiler, Machin-benzeri Formüller adı verilen algoritmalar geliştirerek, daha da yüksek hızlara erişebilmişlerdir. Bu yöntem, bilgisayarların yükselişine kadar en hızlı hesaplama yöntemi olarak kalmıştır ve sonraki 250 yılda, pi sayısını 620. basamağa kadar verebilmiştir (bu, 1946'da Daniel Ferguson tarafından başarılmıştır).

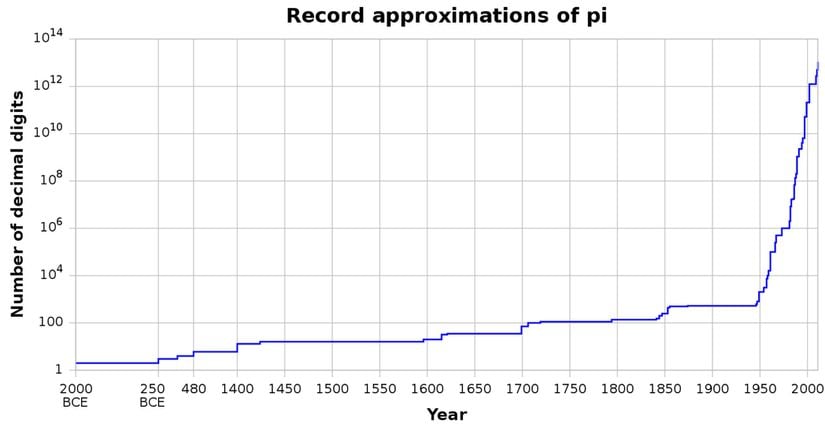
Pi sayısının hesaplanabilen basamaklarının sayısının zamana bağlı olarak değişimi. Sadece bu görseli kullanarak, bilgisayarların hangi noktada icat edildiğini tespit edebilir misiniz?

Bilgisayarların Kattığı Müthiş Hız

Günümüzde matematikçiler, halen pi sayısını gerçek anlamıyla ifade edebilecek yöntemler aramaktadırlar.^{[22], [23], [24]} Bu çaba için artık süperbilgisayarlar kullanılmaktadır ve basamakları keşif çabası halen sürmektedir!

İlk olarak 1949 yılında John von Neumann ve ekip arkadaşları, ENIAC isimli bilgisayarı kullanarak Pi'nin ilk 2037 basamağını ortaya çıkardılar. O zamandan beri çalışan birçok bilgisayar sayesinde:

İlk 1.000.000 basamağı 1973 senesinde keşfettik.
2010 senesinde 2 trilyonuncu basamak keşfedildi.
17 Ekim 2011 günü, Shigeru Kondo, tam 371 günlük süperbilgisayar hesaplaması sonucunda Pi'nin ilk 10.000.000.000.000 (10 trilyon) basamağını açığa çıkardı!
11 Kasım 2016'da, Peter Trueb'in çabaları sayesinde 105 günlük bir hesaplama sonucunda pi sayısının ilk 22.459.157.718.361 (22.4 trilyon) basamağı keşfedildi.
12 Eylül 2021'de, 108 gün süren bir hesaplama sonucunda 62.831.853.071.796 (62.8 trilyon) basamağı keşfedildi.

Pi Sayısının Basamaklarını Kendi Bilgisayarınızda Hesaplayın!

Günümüzdeki algoritmalardan birini kullanmak isterseniz, Gauss-Legendre İteratif Algoritması'nı kullanabilirsiniz. Öncelikle, kullandığınız yazılım dili her ne olursa olsun, şu değerleri tanımlayın:

$p0=1a_0=1, \space b_0=\frac{1}{\sqrt{2}},\space t_0=\frac{1}{4}, \space p_0=1$

Sonrasında, şu sayıları döngüsel bir şekilde hesaplatın:

$an+1=an+bn2a_{n+1}=\frac{a_n+b_n}{2}$

$bn+1=anbnb_{n+1}=\sqrt{a_nb_n}$

$t_{n+1}=t_n-p_n(a_n-a_{n+1})^2$

$p_{n+1}=2p_n$

Bu algoritmayı çalıştırdığınızda, pi sayısı şu şekilde yakınsayacaktır:

$π≈(an+bn)24tn\pi\approx\frac{(a_n+b_n)^2}{4t_n}$

Pi Sayısının Kaç Basamağı Kullanılmalıdır?

Üniversite-öncesi eğitim hayatının en meşhur "geyiklerinden" biri, pi sayısının kaç alınmasıyla ilgilidir: Öncelikle 3 alarak başlanan eğitim hayatı, sonradan 3.1 ve 3.14 şeklinde ilerler. Nihayetinde belirli mühendislik problemleri için üniversitede 3.14159, yani noktadan sonra 5 basamağa kadar kullanılır; tabii bu evrede bilgisayar kullanımı devreye girdiği için, birçok kişi pi sayısını elle girmek zorunda kalmaz.

Merak ediyorsanız, modern bilimin en uç mühendislik konularından olan uzay mühendisliği için NASA, noktadan sonra 15 basamağa kadar kullanmaktadır:

$π=3.141592653589793\pi=3.141592653589793$

NASA'nın Dawn misyonunun direktörü ve baş mühendisi Marc Rayman, bu tercihi şöyle temellendiriyor:^[25]

Neden daha fazla ondalık basamak kullanmadığımızı anlamak için, buna biraz daha yakından bakalım. Sanırım, bilim insanlarının şimdiye kadar gerçekleştirdiği ve noktadan sonra sizin sunduğunuz kadar (noktadan sonra onlarca) basamak sayıyı dahil etmenin gerekli olmadığını, fiziksel olarak gerçekçi hesaplamaları kullanarak bile görebiliriz. Şu örnekleri düşünün:
Tüm Reklamları Kapat
Dünya'dan en uzak uzay aracı Voyager 1'dir. Bu yazının yazıldığı gün itibariyle, yaklaşık 20.1 milyar kilometre uzaktadır. Diyelim ki tam olarak bu büyüklükte (veya 40.2 milyar kilometre çapında) bir yarıçapa sahip bir dairemiz var ve çevreyi hesaplamak istiyoruz, yani $π×yarıçap×2\pi\times\text{yarıçap}\times2$ . Yukarıda verdiğim gibi 15. ondalık basamağa yuvarlanan pi kullanırsak, bu çarpımın 125.5 milyar kilometreden biraz fazla çıktığını görürüz. Burada değerin tam olarak ne olduğuyla (isterseniz çarpabilirsiniz) ilgilenmemize gerek yok; daha ziyade, pi'nin daha fazla basamağını kullanmayarak sebep olduğumuz hatanın ne düzeyde olduğuna bakmamız gerekiyor. Başka bir deyişle, pi'yi 15. ondalık noktasından keserek, o daire için birazcık hatalı bir çevre hesaplamış olduk. Bu hata payı, 40.2 milyar kilometre çapındaki daire için sadece 3,8 santimetre civarındadır. Bunu bir düşünün: Etrafımızda 125.5 milyar kilometreden büyük bir dairemiz var ve bu mesafeyi pi'nin 15 basamağıyla hesaplarsak, serçe parmağınızın uzunluğundan bile daha az hata payımız olacak.
Bunu gezegenimiz Dünya üzerinden de düşünebiliriz: Dünya, ekvatorda 12.755 kilometre çapındadır. O zaman çevresi 40.072 kilometredir. Dünyanın çevresini dolaşsaydınız (ve tepeler, vadiler, binalar gibi engeller, dinlenme durakları, okyanustaki dalgalar vb. göz ardı etseydiniz), bu kadar mesafe katederdiniz. pi'nin az önceki gibi 15 basamağa kadar olan, sınırlı versiyonunu kullansaydınız, kilometre sayacınız ne kadar hatalı olurdu? 1 molekül boyutunda olurdu! Elbette moleküller farklı boyutlarda olabilirler; ama sanıyorum bu, pi'yi 15 basamağa kadar kullanmanın sebep olduğu hata payının küçüklüğü hakkında size bir fikir verir. Bunu görmenin başka bir yolu da, daha fazla pi rakamı kullanmayarak kabullendiğiniz hata miktarının, Dünya çevresindeki yolculuğunuz için bir saç telinden 10.000 kat daha ince olacağıdır!
Gelelim en büyük boyuta: Gözlenebilir Evren'e... Evren'in yarıçapı yaklaşık 46 milyar ışık yılıdır. Şimdi farklı bir soru sorayım: Yarıçapı 46 milyar ışıkyılı olan bir dairenin çevresini bir hidrojen atomunun (en basit atomun) çapına eşit bir doğrulukla hesaplamak için, pi sayısının noktadan sonra kaç tane rakamına ihtiyacımız var? Cevap, 39 veya 40 ondalık basamaktır. Evren'in ne kadar fevkalade uçsuz bucaksız olduğunu bir düşünün - ki Evren, gerçekten de kavrayabileceğimizin çok ötesindedir; hatta en karanlık, en güzel, yıldızlarla dolu gecede bile gözlerinizle görebileceğinizin kesinlikle çok çok çok ötesindedir. Bu kadar devasa bir Evren'de tek bir atom ne kadar inanılmaz derecede küçük olduğunu düşünürseniz, böylesi hassas bir hesap için bile sadece 39-40 basamağın yeterli olduğunu görebilir, dolayısıyla birçok mühendislik uygulaması için sadece 10-15 basamağın fazlasıyla yeterli olduğunu anlayabilirsiniz.

Anlayacağınız, pratik tüm amaçlar için 3.14 bile fazlasıyla yeterlidir; garanticiyseniz 3.14159 alabilirsiniz; NASA seviyesinde hassasiyet istiyorsanız 3.141592653589793 alabilirsiniz.

Bilim Dışında Pi Sayısı

Pi Sayısı ve Müzik

Aşağıda, Pi sayısına dayanarak hazırlanmış bir beste dinleyeceksiniz. Öncelikle sizi besteyle baş başa bırakalım:

Videonun orjinalinde, İncil'den ve çeşitli batıl inançlardan (666 sayısı gibi) örnekler verilmeye zorlanmıştı. Bu sebeple bazılarını gerçek, bilimsel verilerle değiştirdik. Yine de, hoş ve eğlenceli bir video olduğu kanısındayız. Video boyunca verdiğimiz bilgilerin de faydalı olacağı kanısındayız.

Ancak orijinalini görmek isterseniz, buradan izleyebilirsiniz:

Tabii bu müziği kulağa bu kadar hoş getiren başlıca unsurlardan birisi, Pi'nin sayı diziliminin "müzikal" olması falan değildir. Sanatçı, müzikal bilgisi dahilinde hangi sayıları hangi notalara ataması gerektiğini belirlemektedir. Dolayısıyla kulağa hoş gelecek notalar tercih edilmektedir. Daha önemlisi, sol el harmonileri, müzikal değeri arttıracak biçimde belirlenmektedir. Dolayısıyla, her sanatçı bu sayılara farklı notalar atayarak farklı müzikler elde edebilir. Bu müzik, Pi sayısının "evrensel" müziği değildir. Bir diğer örnek buradadır:

Bu Makaleyi Alıntıla

Okundu Olarak İşaretle

Paylaş

Sonra Oku

Notlarım

Yazdır / PDF Olarak Kaydet

Bize Ulaş

Yukarı Zıpla

İçeriklerimizin bilimsel gerçekleri doğru bir şekilde yansıtması için en üst düzey çabayı gösteriyoruz. Gözünüze doğru gelmeyen bir şey varsa, mümkünse güvenilir kaynaklarınızla birlikte bize ulaşın!

Bu içeriğimizle ilgili bir sorunuz mu var? Buraya tıklayarak sorabilirsiniz.

İçerikle İlgili Sorular

Pi sayısı tam olarak nedir?

Soru & Cevap Platformuna Git

Bu İçerik Size Ne Hissettirdi?

Kaynaklar ve İleri Okuma

^ S. Bogart. What Is Pi, And How Did It Originate?. (17 Mayıs 1999). Alındığı Tarih: 2 Kasım 2021. Alındığı Yer: Scientific American | Arşiv Bağlantısı
^ W. Jones. (1706). Synopsis Palmariorum Matheseos. ISBN: 9781354508442. Yayınevi: Palala Press.
^ Math Is Fun. What Is Infinity?. Alındığı Tarih: 2 Kasım 2021. Alındığı Yer: Math Is Fun | Arşiv Bağlantısı
^ Q. Yuan, et al. Is Infinity A Number?. (1 Mayıs 2011). Alındığı Tarih: 2 Kasım 2021. Alındığı Yer: Mathematics Stack Exchange | Arşiv Bağlantısı
^ K. Jay, et al. Difference Between "Infinite" And "Indefinite". Alındığı Tarih: 2 Kasım 2021. Alındığı Yer: English Language & Usage Stack Exchange | Arşiv Bağlantısı
^ Ask a Mathematician. Since Pi Is Infinite, Do Its Digits Contain All Finite Sequences Of Numbers?. (8 Kasım 2009). Alındığı Tarih: 2 Kasım 2021. Alındığı Yer: Ask a Mathematician / Ask a Physicist | Arşiv Bağlantısı
^ B. M. Scott, et al. Does Pi Contain All Possible Number Combinations?. (18 Ekim 2012). Alındığı Tarih: 2 Kasım 2021. Alındığı Yer: Mathematics Stack Exchange | Arşiv Bağlantısı
^ C. Pickover. The 15 Most Famous Transcendental Numbers -. Alındığı Tarih: 2 Kasım 2021. Alındığı Yer: University of Wisconsin | Arşiv Bağlantısı
^ Math Is Fun. Irrational Numbers. Alındığı Tarih: 2 Kasım 2021. Alındığı Yer: Math Is Fun | Arşiv Bağlantısı
^ M. Clagett. (1989). Ancient Egyptian Science. ISBN: 9780871692146. Yayınevi: American Philosophical Society.
^ M. Clagett. (1989). Ancient Egyptian Science: Ancient Egyptian Mathematics. ISBN: 9780871692320. Yayınevi: American Philosophical Society.
^ M. Verner. (2002). The Pyramids: The Mystery, Culture, And Science Of Egypt's Great Monuments. ISBN: 9780802139351. Yayınevi: Grove Press.
^ W. M. F. PETRIE. (1925). Surveys Of The Great Pyramids1. Springer Science and Business Media LLC, sf: 942-943. doi: 10.1038/116942a0. | Arşiv Bağlantısı
^ M. Shermer. (2002). The Skeptic Encyclopedia Of Pseudoscience. ISBN: 9781576076538. Yayınevi: ABC-CLIO.
^ A. J. Wells. (2006). The British National Bibliography.
^ ^a ^b R. Herz-Fischler. (2000). The Shape Of The Great Pyramid. ISBN: 9780889203242. Yayınevi: Wilfrid Laurier University Press.
^ ^a ^b ^c ^d J. Arndt. (2001). Pi - Unleashed. ISBN: 9783540665724. Yayınevi: Springer Science & Business Media.
^ K. Chaitanya. (1982). A Profile Of Indian Culture.
^ E. W. Weisstein. Archimedes Algorithm. Alındığı Yer: Wolfram Alpha | Arşiv Bağlantısı
^ ^a ^b C. B. Boyer. (1991). A History Of Mathematics. ISBN: 9780471543978. Yayınevi: Wiley.
^ P. Eymard. (2005). The Number Pi. ISBN: 9780821832462. Yayınevi: American Mathematical Society.
^ P. Beckmann. (2007). A History Of Pi. ISBN: 9780880294188. Yayınevi: Marboro Books.
^ S. Plouffe. On The Computation Of The N^th Decimal Digit Of Various Transcendental Numbers. (2 Aralık 2009). Alındığı Tarih: 2 Kasım 2021. Alındığı Yer: arXiv.org | Arşiv Bağlantısı
^ J. D. Cook. Best Rational Approximations For Pi. (22 Mayıs 2018). Alındığı Tarih: 2 Kasım 2021. Alındığı Yer: Applied Mathematics Consulting | Arşiv Bağlantısı
^ M. Rayman. How Many Decimals Of Pi Do We Really Need?. (16 Mart 2016). Alındığı Tarih: 14 Mart 2022. Alındığı Yer: NASA JPL | Arşiv Bağlantısı
C. Rossi. (2004). Architecture And Mathematics In Ancient Egypt. ISBN: 9781107320512. Yayınevi: Cambridge University Press.
^ S. Schnell. Pi Is Encoded In The Patterns Of Life. Alındığı Yer: The Biophysical Society | Arşiv Bağlantısı
^ Pi World Ranking List. Pi World Ranking List. Alındığı Yer: Pi World Ranking List | Arşiv Bağlantısı
^ A. Iyer. Do We Have Any Mathematical Proof That Pi Is Infinite?. (31 Mart 2020). Alındığı Yer: Science ABC | Arşiv Bağlantısı
^ F. A. J.. (1964). Theory And Problems Of Differential And Integral Calculus (Schaum's Outline Series). ISBN: 9780070026537.

Evrim Ağacı'na her ay sadece 1 kahve ısmarlayarak destek olmak ister misiniz?

Şu iki siteden birini kullanarak şimdi destek olabilirsiniz:

kreosus.com/evrimagaci | patreon.com/evrimagaci

Çıktı Bilgisi: Bu sayfa, Evrim Ağacı yazdırma aracı kullanılarak 02/12/2023 01:31:04 tarihinde oluşturulmuştur. Evrim Ağacı'ndaki içeriklerin tamamı, birden fazla editör tarafından, durmaksızın elden geçirilmekte, güncellenmekte ve geliştirilmektedir. Dolayısıyla bu çıktının alındığı tarihten sonra yapılan güncellemeleri görmek ve bu içeriğin en güncel halini okumak için lütfen şu adrese gidiniz: https://evrimagaci.org/s/1066

İçerik Kullanım İzinleri: Evrim Ağacı'ndaki yazılı içerikler orijinallerine hiçbir şekilde dokunulmadığı müddetçe izin alınmaksızın paylaşılabilir, kopyalanabilir, yapıştırılabilir, çoğaltılabilir, basılabilir, dağıtılabilir, yayılabilir, alıntılanabilir. Ancak bu içeriklerin hiçbiri izin alınmaksızın değiştirilemez ve değiştirilmiş halleri Evrim Ağacı'na aitmiş gibi sunulamaz. Benzer şekilde, içeriklerin hiçbiri, söz konusu içeriğin açıkça belirtilmiş yazarlarından ve Evrim Ağacı'ndan başkasına aitmiş gibi sunulamaz. Bu sayfa izin alınmaksızın düzenlenemez, Evrim Ağacı logosu, yazar/editör bilgileri ve içeriğin diğer kısımları izin alınmaksızın değiştirilemez veya kaldırılamaz.

Kategoriler ve Etiketler

Tümünü Göster