Oyun Teorisi - 5: Tekrarlı Oyunlar ve Oyunlarda Öğrenme

Giriş

Oyun Teorisi yazı dizimizin bu makalesinde, oyunların tekrar ettiği (yani, birden fazla defa oynandığı) durumları inceleyeceğiz ve bu durumlarda oyuncuların nasıl “öğrenebildiğine” kısa bir bakış atacağız. Başlamadan önce, bu makalenin oyun teorisi yazı dizimizin bir parçası olduğunu hatırlatmak isteriz. Bu yazı dizisinin ilk üç makalesi oyun teorisinin temel kavramlarını ve analiz yöntemlerini tanıtmaktadır ve bu sebeple, onların bu makaleye başlamadan önce okunmasını şiddetle tavsiye ederiz. İlk üçü dışındaki makaleler, temel kavramların üzerine koyulan daha spesifik örnekleri içermektedir ve birbirlerinden bağımsızdırlar. Makalelere aşağıdaki linklerden ulaşılabilir:

• Temel kavramlar ve analiz yöntemleri:
• Oyun Teorisi - 1: Oyunlar ve Oyunların Modellenmesi (https://evrimagaci.org/article/tr/oyun-teorisi-1-oyunlar-ve-oyunlarin-modellenmesi)
• Oyun Teorisi - 2: ''En İyi Cevap'' Konsepti ve Nash Dengesi (https://evrimagaci.org/article/tr/oyun-teorisi-2-en-iyi-cevap-konsepti-ve-nash-dengesi)
• Oyun Teorisi - 3: Strateji Kavramı ve Karma Stratejiler (https://evrimagaci.org/article/tr/oyun-teorisi-3-strateji-kavrami-ve-karma-stratejiler)
• Bağımsız makaleler: Spesifik oyun türleri ve örnekler
• Oyun Teorisi - 4: Bayes Oyunları (https://evrimagaci.org/article/tr/oyun-teorisi--4-bayes-oyunlari)

Tekrarlı Oyunlar

Yazı dizimizde şu ana kadar incelediğimiz oyunlarda, oyuncuların aynı anda (simultane) karar verdiğini/hamle yaptığını ve oyunların sadece bir defa oynandığını varsaydık. Bunların ikisi de gerçek hayatta sık görmediğimiz durumlardır, bu nedenle şu ana kadarki incelemeler okurlarımıza biraz soyut gelmiş olabilir. Oyuncuların sıra ile karar verdiği oyunları, bir sonraki makalemiz olacak olan “Genişletilmiş Formda Oyunlar”da inceleyeceğiz. Bu makalede ise, aynı oyunun birden fazla defa oynandığı durumlara bakarak, analizimizi gerçek hayata biraz daha yakınlaştıracağız. Bu makalenin sonunda, okurlarımıza şu ana kadar soyut gelmiş olabilecek olan oyun teorisinin biraz daha somutlaşmış olacağını ümit ediyoruz.

Belirtmek isteriz ki, bu makalenin içeriği çok geniş bir konu olan Tekrarlı Oyunlar’a bir girişten, birkaç temel kavramın tanıtılması ve birkaç örneğin incelenmesinden ibaret olmakla birlikte; mekanizmanın özünü anlamakta ve bahsettiğimiz somutlaştırmayı başarmakta yeterli olacaktır. Konu üzerine daha ileri bilgi sahibi olmak isteyen okurlarımızı, Kaynaklar ve İleri Okuma kısmındaki kaynaklara başvurmaya veya daha geniş bir araştırma yapmaya davet ediyoruz.

Yukarıdaki paragrafta bahsettiğimiz gibi, gerçek hayatta oyun olarak tanımlayabileceğimiz, birden fazla aktörün birbirleri ile etkileşimini içerek pek çok durum, birden fazla defa gerçekleşir. Söz gelimi, iki insan arasındaki romantik ilişki genelde aylar ya da yıllar mertebesinde sürer ve bu ilişkiler boyunca çiftler, yüzlerce defa birlikte etkinliklere katılırlar. Bunu düşünerek, önceki makalelerde incelediğimiz Cinsiyetlerin Savaşı oyununun ilişki boyunca yüzlerce defa, çeşitli varyasyonlarda oynandığını söyleyebiliriz. Bir hafta sonu sinema/opera ikilemi yaşanırken, öteki hafta sonu Çin restoranı/Meksika restoranı tartışması olabilir. Ya da bir futbolcunun kariyeri boyunca yüzlerce penaltı atışı yaptığını söyleyebiliriz, aynı şekilde iki arkadaşın eğitim hayatları boyunca birbirlerinden dersler konusunda defalarca yardım isteyeceğini öne sürebiliriz. Daha büyük çaplı örnekler vermek gerekirse, hepsi tekrar eden ilişkiler ve etkileşimler ağlarından oluşan pazar hareketlerini, siyasi mücadeleleri, işçi/işveren ilişkilerini düşünebiliriz.

Örnek olarak, aynı ürünü (mesela çikolata) üreten onlarca şirketin arasında imzalanan kurgusal bir anlaşmayı ya da onların kurduğu bir karteli düşünelim. Bu anlaşmanın gereği olarak, dünyadaki çikolata üreticilerinin üretimine bir sınırlama koyularak, çikolata fiyatlarının artmasının amaçlandığını farz edelim. Bu planın gerçekleşmesi için, karteli oluşturan şirketlerin birbirleri ile işbirliği yapmaları ve üretimlerini belirlenen sınırlara çekmeleri gerekmektedir. Bunu başarabilirlerse, uzun vadede karlarını artırabileceklerdir. Lakin, anlaşmayı imzalayan şirketlerden biri veya birkaçı anlaşmayı bozarak gizlice üretimlerini artırabilirler. Diğer üyeler tarafından fark edilmediğini varsayarsak, üretimin artması, kısa vadede oyunbozan şirketin karını artırabilir, ancak uzun vadede, piyasadaki çikolata fiyatlarının istendiği gibi artmamasına sebep olarak, kartelin tüm üyelerinin zararına olabilir.

Dikkatli bakacak olursak, bahsettiğimiz “Kartel Oyunu”nun onlarca/yüzlerce aktörün olduğu devasa bir Tutsak İkilemi olduğunu görebiliriz: Tüm grup için en iyi sonucun alınması için, aktörlerin hepsinin işbirliği yapması gerekmektedir. Ancak işbirliği yapmamak (anlaşmaya ihanet etmek) bireysel olarak tüm aktörler için daha iyi bir sonuç anlamına gelmektedir. Tabii, tüm aktörlerin anlaşmaya ihanet etmesi durumunda, fiyatların anlaşma öncesinde herkesin serbestçe üretim yaptığı duruma geri dönecek olması sebebiyle, kimse kayda değer bir fayda sağlayamayacaktır. Bu anlaşmanın süresi boyunca, anlaşmayı bozma fırsatı aktörlerin önüne defalarca çıkacaktır. Bir nevi, bu fırsatın çıktığı her durumda -söz gelimi, her yönetim kurulu toplantısında- oyuncular bir hamle yapmaktadır: Anlaşmaya ihanet etmeyi ya da devam ettirmeyi seçerler.

Daha önce de bahsettiğimiz gibi, Tutsak İkilemi oyunu, gerçek hayattaki pek çok durumu modellemek ve kabaca incelemek için çok önemli bir araçtır. Neticede gözlemlediğimiz pek çok ilişki, aslında çıkarları birbirleriyle çatışan aktörlerin işbirliği yaparak daha iyi sonuca varmaya çalışmaları üzerine kuruludur. Ne var ki, önceki yazılarda gördüğümüz gibi, oyunun kendi doğasında bir çelişki mevcuttur: Tek bir defa oynandığı durumda oyunun Nash dengesi, tüm oyuncuların anlaşmaya ihanet ettiği ve sonuç olarak herkesin “kaybettiği” sonuçtur. Bu çelişkinin nasıl çözüldüğünü görmek için, oyunun birden fazla defa oynandığı duruma göz atmamız gerekiyor. Bunun için önce tekrarlı oyunları nasıl modelleyebileceğimize bakalım.

Tekrarlı Oyunların Modellenmesi: Sonsuz Tekrarlı Oyunlar, Kazanç ve Kazanç Azalma Katsayısı

Tekrarlı oyunları modellememizde yapacağımız ilk varsayım, oyunun sonsuz defa oynandığı olacaktır. Bu, elbette gerçekçi bir varsayım değil, ancak çok büyük sayılardaki örnekleri sonsuz olarak varsaymak, matematiksel modellerde sık sık kullanılan, hem analizi kolaylaştıran hem de başarılı sonuçlar veren bir araçtır. Ayrıca, birazdan tanımlayacağımız kazanç azalma katsayısı sayesinde, bu “sonsuz”un neden tam anlamıyla bir “sonsuz”u değil, gelecekte sona erebilecek bir oyunu temsil ettiğini de göreceğiz.

Sonsuz defa oynanan bir oyunda, bir oyuncunun tüm tekrarlar boyunca elde ettiği toplam kazançtan bahsetmenin mümkün ve anlamlı olup olmadığı aklınıza gelmiş olabilir: Bu kazanç, pozitif veya negatif sonsuza gidebileceği gibi, sürekli +1 ve -1 arasında gidip gelmesi gibi bir durumda belirsiz de olabilir. Bunun yerine, bir ortalama kazançtan bahsetmek mümkün olabilir: k defa oynanan bir oyunda, bir oyuncunun ortalama kazancı, o oyunlar boyunca elde ettiği toplam kazancın k’ya bölümü olarak tanımlanacaktır. Matematik ile aşina olan okurlarımız, k’nın sonsuza gittiği limiti alarak, sonsuz defa oynanan bir oyun için tanımlı ve anlamlı bir kazanç tanımlamanın mümkün olduğunu görebilirler. Ancak, bizim analizimize ekleyeceğimiz kazanç azalma katsayısı sayesinde, ortalama kazançları hesaplamamıza gerek olmayacak.

Tekrarlı oyunları oynarken, oyuncular stratejilerini, sadece o andaki değil, gelecekteki kazançlarını da düşünerek belirlerler. Çikolata üreticileri kartelinin üyeleri, uzun vadede kazançlarını yükseltmek adına o günkü kazançlarından fedakârlık yapmayı kabul etmişlerdir. Birlikte ders aldığınız arkadaşınıza anlamadığı konularda yardım ederek, onun da gelecekte size başka bir derste yardım etmesini sağlayabilirsiniz. (Özellikle “çan eğrisi” sisteminin uygulandığı üniversitelerde okumuş okurlarımız, bu geri dönen yardım kavramı ile eminiz defalarca karşılaşmıştır.)

Pratikte, neredeyse her zaman, gelecekteki kazançlar şimdikilerden daha değersiz görünür. Bu durumun çok çeşitli şekillerde yorumlamak mümkündür: Oyuncu, çok da mantıklı olmayan “insani” sebeplerle (keyfi o anda alma arzusu, paranın geleceğine güvenmeme tembellik, üşengeçlik, geleceği düşünmeme, hatta doların uzun vadede daima yükselmesi?) geleceğe daha az önem veriyor olabilir. Ya da o anda kazanca daha çok ihtiyacı olduğunu, gelecekte durumunu düzelteceğini (diğer faaliyetlerinden daha fazla para kazanacağını, daha düzenli ders çalışacağını vb.) düşünüyor olabilir.

Evrim Ağacı'ndan Mesaj

Neden Desteğe İhtiyacımız Var?

Aslında maddi destek istememizin nedeni çok basit: Çünkü Evrim Ağacı, bizim tek mesleğimiz, tek gelir kaynağımız. Birçoklarının aksine bizler, sosyal medyada gördüğünüz makale ve videolarımızı hobi olarak, mesleğimizden arta kalan zamanlarda yapmıyoruz. Dolayısıyla bu işi sürdürebilmek için gelir elde etmemiz gerekiyor.

Bunda elbette ki hiçbir sakınca yok; kimin, ne şartlar altında yayın yapmayı seçtiği büyük oranda bir tercih meselesi. Ne var ki biz, eğer ana mesleklerimizi icra edecek olursak (yani kendi mesleğimiz doğrultusunda bir iş sahibi olursak) Evrim Ağacı'na zaman ayıramayacağımızı, ayakta tutamayacağımızı biliyoruz. Çünkü az sonra detaylarını vereceğimiz üzere, Evrim Ağacı sosyal medyada denk geldiğiniz makale ve videolardan çok daha büyük, kapsamlı ve aşırı zaman alan bir bilim platformu projesi. Bu nedenle bizler, meslek olarak Evrim Ağacı'nı seçtik.

Eğer hem Evrim Ağacı'ndan hayatımızı idame ettirecek, mesleklerimizi bırakmayı en azından kısmen meşrulaştıracak ve mantıklı kılacak kadar bir gelir kaynağı elde edemezsek, mecburen Evrim Ağacı'nı bırakıp, kendi mesleklerimize döneceğiz. Ama bunu istemiyoruz ve bu nedenle didiniyoruz.

Destek Ol

• Ama bunlardan daha ilginç bir yorum, aktörün geleceğe en az şu an kadar önem vermesine rağmen, oyunun kendisinin geleceğine güvensizlik duyuyor olabileceği yorumudur. Oyuncu, görünürde sonsuz defa oynanan bir oyunun, belli bir süre sonra biteceğine inanıyor ya da bitmesi ihtimalinin olduğunu düşünüyor olabilir. Buna örnek olarak, bir insanın bundan on-yirmi yıl sonra ölme ihtimali olduğunu düşünmesi, bir öğrencinin eğitim hayatına devam edip etmeyeceği yönündeki kararsızlığı, ya da karteldeki şirketlerin kartelin devam edip etmeyeceği konusundaki endişesi verilebilir. Tüm bunları hesaba katarak, oyuncuların gelecek kazancındaki bir azalmayı temsil edecek bir kazanç azalma katsayısı olarak ß’yı tanımlayabiliriz. Bu ß ile, sonsuz defa tekrar eden bir oyunu oynayan oyuncunun bugünkü ve gelecekteki toplam kazancı, şu şekilde ifade edilir:

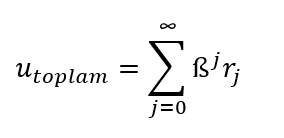
(Sigma -Σ- işaretinin, sonrasında gelen terimlerin, üstünde ve altında tanımlanan aralık boyunca toplanması anlamına geldiğini hatırlayınız.)

Bu sonsuz toplamda:

• j oyunun (ilk tekrarın numarası 0 olmak üzere) kaçıncı tekrarı olduğunu belirtmektedir.
• Her r_j, j’inci tekrarda bahsi geçen oyuncunun elde edeceği kazancı göstermektedir.
• Bu kazanç, azalma katsayısı ß’nın j’inci kuvvetiyle çarpılmaktadır.

Tanımı ve modellediği olgu gereği ß, daima 1’den küçük olacaktır. Sözgelimi, ß’nın 0.7 olması, oyuncunun geleceğe o günden %30 (1-0.7=0.3) daha az değer verdiği veya oyuncuya göre oynanan oyunun bir tur sonra bitmesine %30 olasılık vermesi (örneğin, yaşlı bir patron bir sene içinde ölmesine %30 olasılık veriyor) anlamına gelebilir. ß 1’den küçük olacağı için, şimdiki zamandan bakan bir oyuncu için, kazancı geleceğe gittikçe sürekli azalmaktadır. Eğer bir oyuncu için ß=0.5 ise, oyuncu altı tur sonraki kazancına şimdiki kazancının (0.5)⁶=0.0156’sı kadar önemsemektedir, yani yaklaşık %1.5’u kadar! Nihayetinde, çok uzak bir gelecekte yaşanacak bir tekrardaki kazancına oyuncu neredeyse hiç değer vermeyecektir, yani ihmal edilebilir olacaktır. Bu azalma katsayısı, sonsuz oyun varsayımımızın neden gerçekten uzak olmadığını da ortaya koyuyor: Zaten belli bir tekrardan sonra oyunun oynanıp oynanmamasının (şimdiki zamandan bakınca) bir önemi yoktur, bu tekrarlarda alınacak kazançların oyuncunun şu andaki stratejisine etkisi ihmal edilebilir.

Bu kazanç azalma katsayısı sayesinde, artık toplam kazançların sonsuza gitmesi sorunundan kurtuluyoruz. Matematikle aşina okurlarımız, bunun sonsuz seri toplamları sayesinde mümkün olduğunu görebilirler. Gereksiz kalabalık olmaması adına, sonsuz seri toplamlarından bu makalede bahsetmeyeceğiz. Birazdan bunu tekrarlı Tutsak İkilemi üzerinde de göreceğiz.

Gerekli kavramları tanımladığımıza ve tekrarlı oyunları nasıl modelleyebileceğimizi gördüğümüze göre, bu modeli tekrarlı Tutsak İkilemi’ne uygulayabiliriz.

Tekrarlı Tutsak İkilemi

Tutsak İkilemi’nin tekrarlandığı durumu incelemeden önce, oyunu hatırlayalım. Aşağıda, Tutsak İkilemi’ni normal formda gösterilmiş olarak görüyoruz. Bu gösterimde, analizimizde negatif sayılarla uğraşmamak adına, kazançları pozitif olacak şekilde biraz farklı ifade ettik. Bu farklı kazanç değerleri ile de oyunun yapısındaki temel özelliklerinin (hamleler, göreli kazançlar, optimum sonuç, en iyi cevaplar, Nash dengesi) ilk kullandığımız versiyonu ile aynı şekilde olduğunu göstermek mümkündür. Bu yüzden, değişen bir şey olmadığını varsayabiliriz. Kazanç değerleri dışında, görselde kazanç azalma katsayısı ß’yı da görüyoruz. Bu ß değerlerinin stratejileri nasıl değiştirebileceğini inceleyeceğimiz için, onları belirsiz olarak bıraktık.

Daha önce de gördüğümüz gibi, bu oyunun bir defa oynandığı durumda Nash dengesi, iki oyuncunun da döneklik yaptığı durumdur. Peki oyunu sonsuz defa oynadığımızda ne olacaktır? Bir defa oynanan durumun aksine, sadece oyuna ve kazanç azalma katsayılarına bakarak kesin bir cevap veremeyiz: Sonsuz defa oynanan bir oyunda, sonsuz tane denge olabilir. Önceki makalelerde kullandığımız yöntemlerle bu dengeleri bulamayız, çünkü artık stratejiler sınırlı sayıdaki hamlelerin belirli olasılıklarla oynanmasından ibaret değil. Sonsuz tane strateji yazabiliriz. Bir oyuncunun 1, 2, 3. tekrarlarda işbirliği yapıp sonra döneklik etmesi de bir stratejidir, 1, 2 ve 4. tekrarlarda işbirliği yapması da, 1, 3, 4’te de, sadece 17 ve 32’nin ortak katlarında döneklik yapması da… Bunların hepsi sonsuz sayıda elemanı olan bir strateji uzayının bir parçasıdır.

Bunun yerine, tahmin ve gözlemlerimizden yola çıkarak ya da akıl yürüterek, oynanacağını düşündüğümüz stratejilerin denge olup olmadığını, ya da hangi şartlarda denge olacağını inceleyebiliriz. Böyle bir stratejiye, oyun teorisi terminolojisinde tit-for-tat olarak bilinen strateji örnek verilebilir. Bu stratejide, oyuncular işbirliği yaparak başlar. Eğer bir oyuncu döneklik yaparsa, diğer(ler)i sonraki turda (veya sonraki belli bir sayıdaki turda) döneklik yaparak o oyuncuyu “cezalandırır.” Bu cezalandırma bittikten sonra da yeniden işbirliğine dönerler. Bunun gerçek hayattaki bir karşılığı (tam olarak olmasa da) kartelin anlaşmasını bozduğu fark edilen bir üyenin “makul” bir cezaya çarptırılması ve sonra da üyeliğinin devam etmesi olabilir.

Bir diğer strateji ise, oyuncuların işbirliği yaparak başlaması, ancak bir oyuncu döneklik yaparsa diğer oyuncuların da oyunun kalanı boyunca döneklik etmesi olabilir. Acımasız tetik (grim trigger) olarak bilinen bu stratejiye örnek, bir üyenin anlaşmayı bozması durumunda kartelden atılması ya da kartelin tümüyle dağılması olabilir. Biz, burada, acımasız tetik stratejisinin sonsuz defa tekrar edilen Tutsak İkilemi’nde nasıl bir sonuç vereceğini inceleyeceğiz ve modelimizin sezgisel olarak da tutarlı olduğunu göreceğiz.

Öncelikle, eğer oyunculardan biri döneklik ederse, diğer oyuncunun da cevap olarak döneklik edeceğini hatırlayalım. Bu sebeple, uzun vadede oyun ya işbirliği-işbirliği ya da döneklik-döneklik şeklinde devam edecektir. Bunun yanında, eğer bir oyuncu bir şekilde ötekinin döneklik edeceğini düşünüyorsa, o da döneklik edecektir. Bu durumlarda sonuç barizdir. Şimdi, diğer oyuncunun işbirliği yaparak başladığını düşünerek, herhangi bir oyuncunun gözünden bakalım: Acımasız tetik stratejisinde, oyuncu eğer işbirliği yaparsa elde edeceği kazanç aşağıdaki toplamla ifade edilebilir:

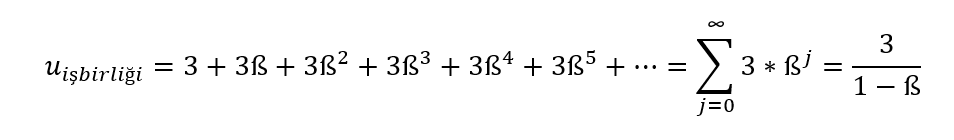
Oyuncu, oyunun tamamını işbirliği yaparak devam ettirirse, 3/(1- ß) kazancına sahip olacaktır. (Bunu, ilgili sonsuz toplam formülünü kullanarak hesapladık.) Yani, oyuncunun uzun dönemde toplam kazancı ß’ya bağlıdır. ß azaldıkça, yani oyuncu bugüne geleceğe kıyasla daha çok değer verdikçe, payda büyüyecek, kesir küçülecek ve işbirliği ile elde edilecek kazanç azalacaktır. Sezgisel olarak da beklediğimiz bir durumdur bu.

Benzer şekilde, oyuncunun ilk turda döneklik yaptığı duruma bakarsak, oyuncunun kazancı aşağıdaki gibi ifade edilebilir:

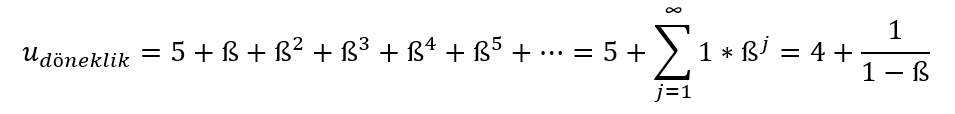
Bu durumda, oyuncu ilk turda 5 kazanç sağlarken, sonraki her turda 1 kazanç almaktadır. İlgili toplam formülünü yeniden uyguladığımızda da en sağdaki sonuç elde edilmektedir. Dikkat edilirse, bir kez daha ß, yani geleceğe verilen önem azaldıkça döneklikten alınacak kazanç azalmaktadır. Bu normal, çünkü daha az da olsa, oyuncu hala gelecekteki tekrarlardan pozitif (+1) fayda sağlamaktadır. Ancak, işbirliğinin kazancının ß ile azalma hızı, dönekliğin kazancının azalmasından daha hızlıdır, çünkü azalan terim ilkinde 3, ikincisinde ise 1 katsayısıyla çarpılmaktadır.

Agora Bilim Pazarı

Amerikan Keneviri

Devamını Göster

₺480.00

Satın Al Tüm Ürünler

• Dış Sitelerde Paylaş

Şimdi, işbirliği yapmanın döneklik yapmaya kıyasla ne kadar kazançlı olduğuna bakalım:

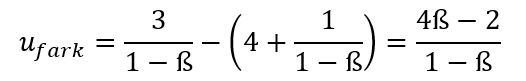
Geleceğe belirli bir önem veren, yani belirli bir ß katsayısına sahip olan bir oyuncu, işbirliği yaparsa, döneklik ettiği duruma kıyasla (4ß-2)/(1-ß) kadar kazanç sağlayacaktır. Eğer bu değer 0’dan büyükse, oyuncu işbirliği yapacaktır, küçükse ise döneklik edecektir. Yani oyuncunun işbirliği yapması için:

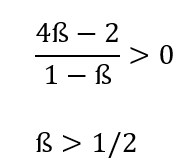
Şartının sağlanması gereklidir. Oyuncu, eğer geleceğe bugünün en azından yarısı (%50’si) kadar güveniyorsa işbirliği yapacaktır. Eğer daha az değer veriyor ise, döneklik ederek bugün alacağı 5 kazancı tercih edecektir. Bu beklentimizle de uyuşuyor: Yüksek ß değerlerinde oyuncu işbirliği yapmaya yatkınken, düşük ß değerlerinde değildir; yani geleceğe güven azaldıkça, oyuncu gelecekte de kazancını devam ettirmek adına bugünden fedakarlık yapmaya daha az yatkındır.

Burada unutmamamız gereken, bu analizi yaparken, oyuncunun gözünden ve bugünden, geleceğe bakıyor olduğumuzdur. Bu “bugün,” oyunun herhangi bir anına denk gelebilir. Zaman içinde şartların değişmesi ise, oyunun yapısını değiştirebilir. Örneğin, diyelim ki kartel oyununu inceliyoruz. Bir oyuncu, geleceğe bugünün %60’ı kadar değer veriyor, yani ß=0.6. Bu durumda, oyuncu kartelin ilk kurulduğu durumda döneklik etmemeyi tercih edecektir. Varsayalım ki, birkaç yıl sonra bu şirketin bünyesinde çalışan AR-GE bölümünde, şirketin üretim masraflarını büyük ölçüde düşürecek bir teknoloji geliştirildi. Böylece, üreticinin anlaşmayı bozması ile elde edeceği kazanç, 5’ten 10’a yükseldi. Yukarıdaki ile benzer bir analiz, bu durumdan sonra işbirliğine devam etme şartını

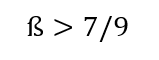
yani ß’nın kabaca %77’den büyük olması olarak gösterir. Oyuncu için ise geleceğe verilen önem bugüne kıyasla sadece %60’dır. Bu yüzden, o ana kadar anlaşmada olan bir şirket, yeni teknolojiden (veya başka bir değişimden) sonra anlaşmadan ayrılabilir.

Gördüğümüz üzere, tekrar ettiği durumda Tutsak İkilemi’nin çelişkisi, geleceğe verilen önemin ne kadar olduğuna göre çözülebilir. Eğer oyuncular sadece bugün değil, gelecekte de elde edecekleri kazançlara önem veriyorlarsa, işbirliği yaparak tüm oyuncular için en iyi sonucu elde etmeye çalışacaklardır. Ancak bugüne verilen önem geçmişe verilene kıyasla çok daha fazlaysa, döneklik edip bugünün kazancını toplamak cazip olacak ve sonunda yine herkes için kötü sonuca ulaşılacaktır.

Tekrar Eden Oyunlarda Öğrenme

Tutsak İkilemi, uzun vadede daha iyi bir sonuca ulaşmak için işbirliği gerektiren bir oyundu. Peki ya, saf rekabete dayalı oyunlarda durum ne olur? Daha önce, bu tip oyunlarda (penaltı vuruşu, para eşleme, taş-kâğıt-makas vb.) oyuncuların belli bir rastgeleliğe sahip karma stratejiler uyguladığını görmüştük. Bu karma stratejileri ise, zamanla oluşacak denge veya bir başka deyişle oyun çok fazla defa oynandığında nihayetinde gözlemleyeceğimiz hamle oynanma sıklığı olacağını söylemiştik. Bu ifade doğru mudur? Acaba oyuncular, zamanla karşılarındakinin hamlelerini gözlemleyerek, kendi hamlelerini ona göre mi ayarladıklarında karma strateji Nash dengesini gözlemlemeye mi başlarız?

Buna bakabilmek için, oyunlarda öğrenmenin nasıl olduğunu tanımlamamız gerekiyor. Oyun teorisinde öğrenme modelleri oldukça zengin bir konu olmakla birlikte, bu Nash dengesi incelemesi için basit ve sıklıkla başvurulan Hayali Oyun modelini kullanabiliriz. Bu modelde:

• Oyuncu, oyuna rakibinin stratejisi ile ilgili bir önyargı ile başlar.
• Bu önyargı, her tekrar ile güncellenir ve oyuncunun rakibinin hamlelerini gözlemlemesi ile değişir.
• Oyuncunun gözlemi, zamanla rakibin stratejisini gözlemleyip tahminlerini ona göre düzenlemesini ve kendi stratejisini bu yönde geliştirmesini sağlar.

Bunu basitçe matematik diline dökelim:

• s_tahmin, oyuncunun rakibinin stratejisi hakkındaki tahmini olsun.
• s_tahmin(a), oyuncunun rakibinin a aksiyonunu oynamasına verdiği olasılığı ifade etsin.
• g(a) oyuncunun rakibinde a aksiyonunu o ana kadar gözlemlediği tekrar sayısı olsun.

Gösterimi basitleştirmek için oyuncunun ilk baştaki önyargısını ihmal edersek (bunun aslında ilerleyen tekrarlarda nasıl önemsiz kalacağını birazdan bakacağımız örnekte göreceğiz) şu şekilde bir ilişki kurabiliriz:

Yani, oyuncu, rakibinin stratejisini tamamen istatistiksel olarak tahmin etmektedir. Şimdi, Hayali Öğrenme modeli ile öğrendiği varsayılan iki ajanın oynadığı bir para eşleme oyununda ne olduğuna bakalım.

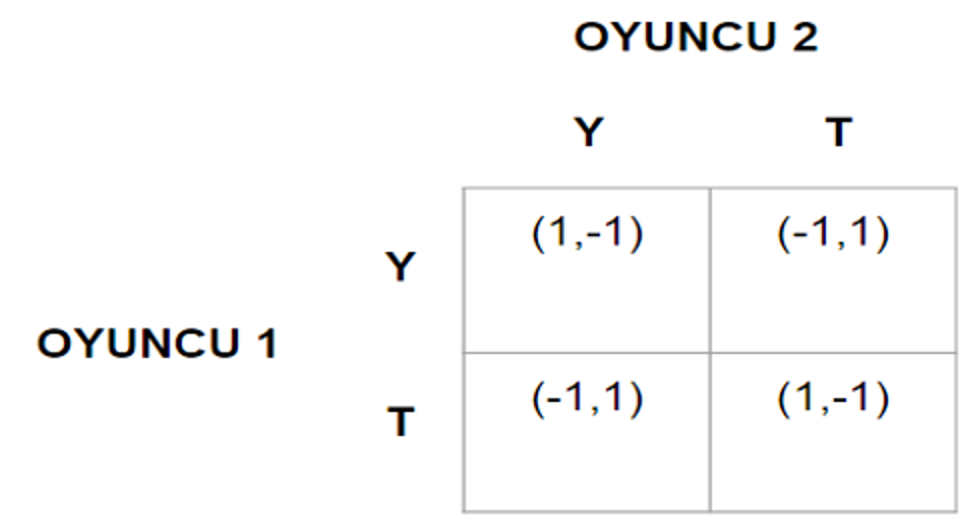
Para eşleme oyununda kazançlar simetrik (-1 veya +1) olduğu için, oyuncuların oynayacağı hamle, tamamen rakiplerinin hangi hamleyi oynamasına daha fazla ihtimal verdiklerine göre şekillenecektir: Oyuncu 1, paraları tutturmak için, Oyuncu 2’nin stratejisinin yazıya ağırlık verdiğini düşünüyorsa yazı, turaya ağırlık verdiğini düşünüyorsa tura oynayacaktır. Oyuncu 2 için ise tam tersi geçerlidir.

Bir not düşelim: Bir önceki Tutsak İkilemi incelemesinin aksine, şu anda oyuncuların oyun boyunca oynayacakları stratejiyi çözümlemeye çalışmıyoruz. Burada yaptığımız, oyuncuların diğer aktörlerin davranışlarından nasıl öğrendiğini gözlemlemek. Bu yüzden her tekrarda oyunu “durdurup,” stratejilerinin ve önyargılarının nasıl şekillendiğine bakacağız. Ayrıca, yine aynı sebeple bir ß değerimiz olmayacak, çünkü her tekrarda “bugünden” bakıyor olacağız.

Yukarıda tanımladığımız şekilde işleyen bir öğrenme mekanizmasının aktif olduğu Para Eşleme oyununu izlemek için, oyunun MATLAB’da ufak bir simülasyonunu yürütebiliriz. Bu simülasyonda, oyun 10,000 defa oynanmıştır. Oyuncuların, ilk başta rakiplerinin hamleleri ile ilgili bir önyargıları mevcuttur ve bu önyargılar 0 ile 1 arasında rastgele belirlenmiştir. Bu önyargılar, oyuncuların rakiplerinin hamlelerini gözlemlemesi ile değişmekte, yukarıdaki kurala göre güncellenmektedir. (Bizim simülasyonumuzda rastgele belirlenen değerler şu şekildedir: Oyuncu 1, rakibinin %15 olasılıkla yazı oynayacağını düşünüyor, Oyuncu 2 ise rakibinin %26 olasılıkla yazı oynayacağını düşünüyor.) Oyuncular, giderek güncellenen bu önyargılar doğrultusunda kendi hamlelerini yapıyorlar: Sözgelimi Oyuncu 1, rakibinin yazı oynamasına tura oynamasından daha fazla ihtimal veriyorsa kendisi de yazı oynayacaktır. Aşağıdaki grafikte,, bu simülasyondaki 10,000 tekrar boyunca Oyuncu 1’in önyargılarındaki değişimi görüyoruz.

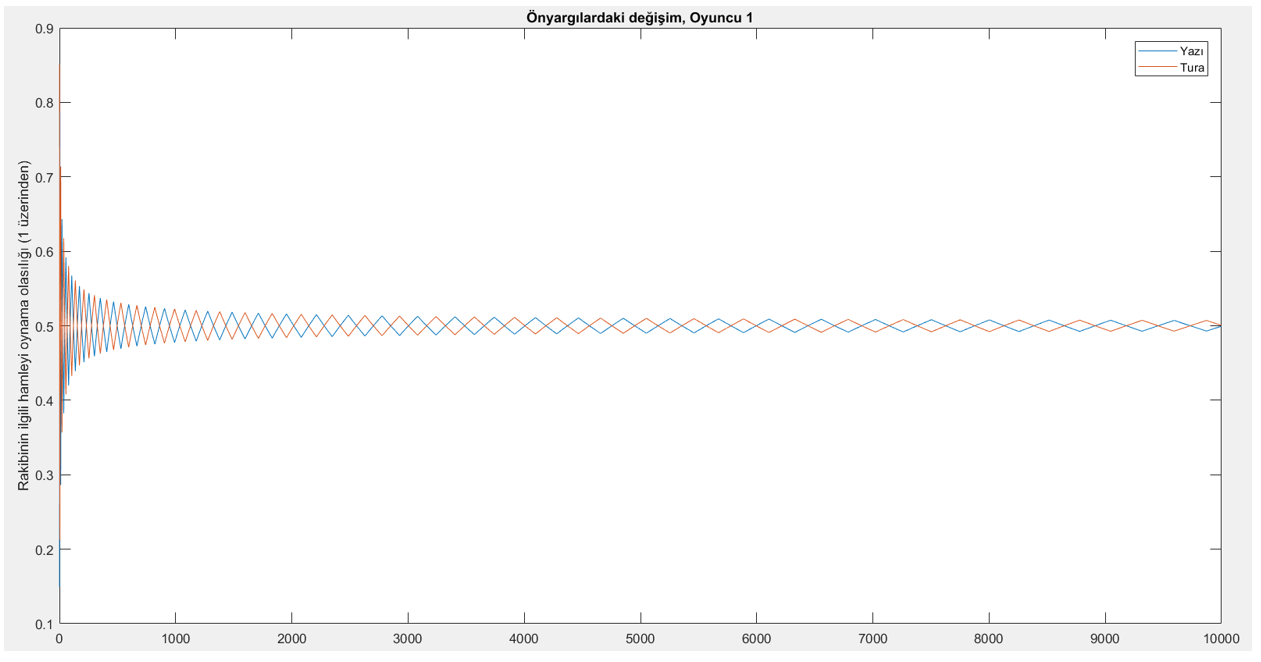
Açık bir şekilde, Oyuncu 1’in inançlarının oyun ilerledikçe 0.5’e (%50’ye) yakınsadığını görüyoruz. Peki Oyuncu 2 için de durum aynı mıdır? Bakalım.

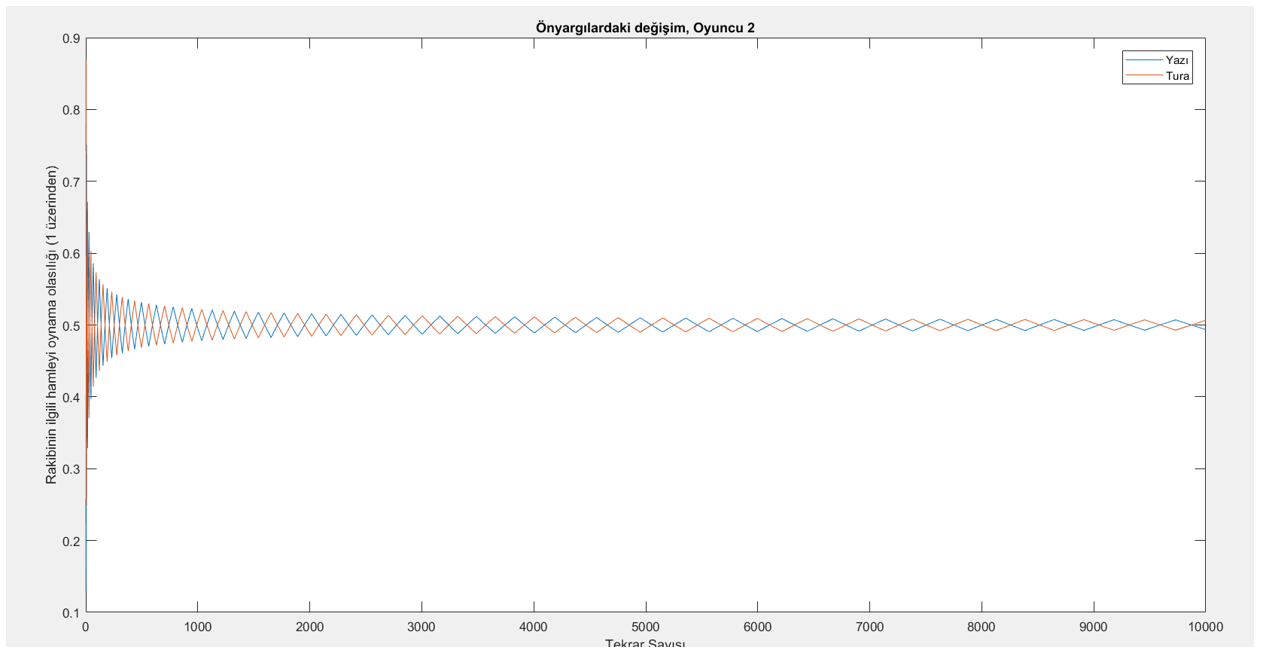
Evet: Oyuncu 1’in de, 2’nin de rakibin stratejisi hakkındaki düşünceleri, Hayali Oyun öğrenmesi ile güncellendiğinde, giderek %50’ye yakınsamaktadır. Buna göre, kendi stratejileri de yaklaşık %50 sıklıkla yazı, %50 sıklıkla tura oynayacakları şekilde değişmektedir. (Kalabalık olmaması adına bu sonuçları göstermiyoruz, ancak oyuncuların rakibinin hangi hamleyi yapması ihtimalinin daha yüksek olduğuna inanmasına göre hamlelerini seçtiklerini düşünürsek, grafikteki kırmızı ve mavi çizgiler neredeyse eşit aralıklarla birbirlerinin altında/üstünde oldukları için iki hamlenin de iki oyuncu tarafından da aynı sıklıkla oynanacağı sonucuna varabiliriz.) Bu sonuçta şaşılacak bir şey yoktur: 0.5 yazı / 0.5 tura oynamak zaten teorik hesabımızda da Para Eşleme oyununun Nash dengesi olarak bulunmuştu. Üçüncü yazımızda, karma strateji Nash dengesinin, oyunun defalarca oynanması durumunda gözlemleyeceğimiz hamlelerin görülme sıklığı olarak yorumlanabileceğimizi söylemiştik. Tekrarlı oyunlardaki öğrenme modeli ile yapılan simülasyonumuz da bunu doğrulayarak, bize Oyun Teorisi’nin gücünü bir kez daha gösteriyor. Elbette, burada Para Eşleme oyunu simetrik olduğu için analiz ve simülasyon kayda değer ölçüde basitleşti. Dileyen okurlarımız, benzer bir simülasyonu kâğıt üstünde veya MATLAB gibi bir uygulamada, simetrik olmayan bir oyun için yürütebilir. O zaman göreceğiniz sonuç da, bu simetrik olmayan oyunun teorideki karma strateji Nash dengesine yakınsayan bir önyargı dağılımı olacaktır.

Sonuç

Bu makalede, şu ana kadar incelediğimiz oyunların tekrar etmesi durumunda (ki oyunların tekrar etmesi, gerçek hayatta sık sık karşılaştığımız bir durumdur) neler olacağını gördük. İlk önce, tekrar eden oyunları nasıl modelleyebileceğimizi gördük. Buna örnek olarak, meşhur Tutsak İkilemi oyununu sonsuz defa tekrar eden, ancak oyuncuların geleceğe geçmişe kıyasla giderek daha az değer verdiği bir oyun olarak modelledik ve bu durumda ortaya nasıl bir denge çıkabileceğini inceledik. Tutsak İkilemi’nin tekrarlı halini incelemek iki açıdan önemlidir: İlk olarak, bu oyunun neden bu kadar güçlü ve genellenebilir bir model olduğunu gördük. Tekrarlandığında Tutsak İkilemi, bir ticaret anlaşmasından arkadaşlar arası bir ders yardımlaşmasına kadar, içinde rekabet ve işbirliğini barındıran pek çok sosyal etkileşime uyarlanabilen bir model olarak karşımıza çıkar. İkinci olarak da, bu oyunun doğasında barındırdığı çelişkinin (oyunun tek Nash dengesinin, tüm aktörlerin zararına olan durum olması) nasıl çözülebileceğini, oyuncuların hangi durumlarda işbirliğine yanaşabileceğini gördük. Kim bilir, belki de dünyadaki tüm sorunları çözmek için yapmamız gereken tek şey, insanların geleceğe olan inançlarını artırmak ve bugünün ötesine bakmalarını sağlamaktır?

Makalenin ikinci kısmında ise, tekrarlı oyunlarda öğrenmenin nasıl işleyebileceğine bakarak, spesifik bir öğrenme modelini Para Eşleme oyununa uyguladık. Bu öğrenmenin sonucunda, oyundaki hamlelerin oyunun karma strateji Nash dengesine yakınsadığını gördük. Bu, üçüncü makalede sezgisel olarak ortaya attığımız bir sonucun empirik gözlemiydi: O makalede, bir defa oynanan bir oyun için anlamsız görünebilen karma strateji Nash dengesinin, oyun defalarca oynandığında hamlelerin gözlemlenme sıklığı anlamına gelebileceğini öne sürmüştük. Yaptığımız basit simülasyonda, gerçekten de öğrenme ile ilerleyen Para Eşleme oyununun Nash dengesine yakınsadığını gözlemledik.

Bu makalenin, özellikle oyunların tekrar etmesi durumunu incelemesi, oyunlarda öğrenmenin nasıl işlediğini göstermesi ve karma strateji Nash dengesinin “görülme sıklığı” yorumunun tutarlılığını incelemesi ile, okurlarımızın aklında kalan bazı soyut noktaları somutlaştırdığını ümit ediyoruz. Bir sonraki makalemizde, oyuncuların hamlelerini aynı anda (simultane) değil, birbirlerinin ardından yaptıkları oyunlar olan Genişletilmiş Formdaki Oyunlar’a bakacak, böylece yine soyut kaldığını düşündüğümüz bazı noktaları açıklığa kavuşturmaya çalışacağız.