Oyun Teorisi - 4: Bayes Oyunları

Giriş

Herkese yeniden merhabalar. Oyun Teorisi yazı dizimizin bu bölümünde, artık spesifik oyun türlerine bakmaya başlayacağız ve bunların ilki de Bayes Oyunları olacak. Bunu yaparken “oyun” anlayışımızı bir yandan daraltırken, bir yandan da genişleteceğiz. Esasında özel bir oyun türü olsa da, Bayes oyunları gerçek hayattaki pek çok durumda geçerli olan oyun türüdür. Hatta, daha ileri gidip, karşımıza çıkan neredeyse tüm oyunların bir Bayes oyunu olduğunu, ve Bayes oyunu olmayan oyun modellerinin sadece analizi kolaylaştıran ve ifadeyi basitleştiren birer “idealleştirme” olduğunu iddia edebiliriz. (Tıpkı mekanik analizlerde yerçekimi ivmesini yüksekliğe bağlı değil de sabit almak gibi.)

Örnek olarak, Oyun Teorisi’nde (özellikle mekanizma tasarımı alanında) oldukça popüler bir araştırma konusu olan açık artırmaları düşünelim. Klasik bir İngiliz açık artırmasına bakalım: Satıcı, belli bir fiyattan artırmayı başlatır, ve talipler de bağırarak (artan sırayla) vermeye gönüllü oldukları miktarı söylerler, bildiğimiz “Var mı artıran?” meselesi anlayacağınız.

Böyle bir açık artırmada, henüz “oyun” başlamadan, artırmayı kazanmak için ne kadar para teklif etmeniz gerektiğini bilmenizin bir imkanı var mıdır? Tabii ki hayır! Zira bunu kesin olarak bilmeniz için, diğer yarışmacıların satılan ürüne ne kadar değer biçtiklerini ve bu bağlamda ne kadar teklif etmeye razı olduklarını bilmeniz gerekiyor, ancak bunu bilmenizin hiçbir yolu yok. Bir başka deyişle, hangi fiyatın size oyunu kazandıracağını bilmeniz için, diğer oyuncuların da “kazançlarını” bilemeniz lazım, ama bilmiyorsunuz.

Bayes Oyunları

Açık artırmalar, Bayes oyunlarına bulunabilecek örneklerden sadece biridir. Bu oyunların en genel tanımı, oyuncuların hangi oyunu oynadıklarını bilmedikleri oyunlardır. Ortada, oynanma ihtimali olan sonlu veya sonsuz sayıda oyun vardır, ve her oyuncunun da hangi oyunu oynadığı yönünde belli inançları vardır: Yine, bir olasılık dağılımı olarak.

Açık artırmalarda, her bir oyuncunun seçebileceği (teoride) sürekli bir değer aralığı olduğu için, oyuncular sonsuz sayıda oyun oyundan hangisi oynadıklarını bilmemektedir. Bu, açık artırmayı Bayes oyunları kategorisine sokar. Tabii, bu durumu “oynanılan oyunun belirsiz olması” şeklinde yorumlamak, bazı okurlarımızın kafasını karıştırmış olabilir. Bu yüzden, daha somut bir örnek verelim.

Şu hikayeyi düşünelim: Bir arkadaşınız, sizi kendi arkadaşlarının olduğu bir yere davet ediyor. Oradaki insanların hemen hiçbiriyle daha önce konuşmuşluğunuz yok; düşüncelerini, görüşlerini bilmiyorsunuz. Muhabbet dönüp dolanıp, en sonunda siyasete bağlanıyor ve bir noktada, sizin de görüşünüz soruluyor. Oradaki insanların düşüncelerini bilmediğiniz için, neyin hoş karşılanıp neyin karşılanmayacağını, ne derseniz kavga çıkabileceğini, ne derseniz de yeni tanıştığınız insanların size sıcakkanlı davranacağını bilemiyorsunuz. Belirtebileceğiniz görüşleri en basit tabirle “sağ” ve “sol” olarak ayırırsak, şöyle bir durumdasınız:

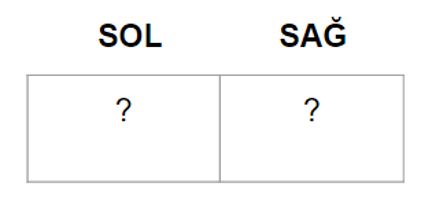
Oyuncular belli, (bu durumda sadece siz, zira hamle yapacak olan tek kişi sizsiniz) yapılabilecek hamleler belli, ama kazançlar hakkında hiçbir fikriniz yok. Bu oyunu, eğer ortamdaki diğer insanların politik görüş olarak aynı fikirde olduğunu varsayarsak, ve yine muhtemel görüşleri sağ ve sol olarak ikiye ayırırsak, şu şekilde de gösterebiliriz:

Bu gösterimde, iki farklı oyun görüyoruz. Oyunlar, birbirlerinden sadece kazanç yönünden ayrılıyor (eğer aynı görüşü söylerseniz diğerleri tarafından sıcak karşılanıyorsunuz, eğer farklı görüş belirtirseniz dayak yiyorsunuz) ve sizin, hangi oyunu oynadığınıza (yani, diğerlerinin sağ görüşte mi sol görüşte mi olduğuna) dair belli bir inancınız var. (Bu durumda, masadakilerin sol görüşte olmasına %60 ihtimal veriyorsunuz.)

Muhtemelen, Bayes oyunlarının neler olabileceğine dair kabaca bir fikriniz oluşmuştur. Gördüğünüz gibi, pratikte karşılaştığımız neredeyse her durum Bayes oyunlarına birer örnektir: Hiçbir durumda, kendi kazançlarımızdan (veya diğer oyuncuların kazançlarından) yüzde yüz emin olamayız. Lakin, bu pratikte karşılaşılan durumların hepsinin teoride bir Bayes oyunu olarak incelenmesinin anlamlı olduğu anlamına gelmiyor, zira buna kalkışacak olursak, yüzlerce parametreyi göz önüne almamız gerekebilir. (Örneğin, Cinsiyetlerin Savaşı oyununda, tarafların partnerlerine ne kadar bağlı olduğu veya tercih ettikleri aktiviteden ötekine kıyasla ne kadar zevk alacakları, kazançları etkileyebilecek bir çok parametreden sadece biridir.) Onun yerine, belirsizliklerle ilgili mantıklı varsayımlar yaparak, sadece önemli, büyük bilinmezleri ayrı oyunlar olarak modellemek daha kullanışlı olacaktır.

Aklınızda oluşmuş olabilecek bir başka soru işareti de, oyunların neden birbirlerinden sadece kazanç olarak ayrılması gerektiği olabilir. Bunun cevabı için de, en başa, oyunları nasıl tanımladığımıza dönmemiz lazım.

Normal formda bir oyunu tanımlarken, üç şeye ihtiyacımız olduğundan bahsetmiştik. Bunlar,

Evrim Ağacı'ndan Mesaj

Neden Desteğe İhtiyacımız Var?

Aslında maddi destek istememizin nedeni çok basit: Çünkü Evrim Ağacı, bizim tek mesleğimiz, tek gelir kaynağımız. Birçoklarının aksine bizler, sosyal medyada gördüğünüz makale ve videolarımızı hobi olarak, mesleğimizden arta kalan zamanlarda yapmıyoruz. Dolayısıyla bu işi sürdürebilmek için gelir elde etmemiz gerekiyor.

Bunda elbette ki hiçbir sakınca yok; kimin, ne şartlar altında yayın yapmayı seçtiği büyük oranda bir tercih meselesi. Ne var ki biz, eğer ana mesleklerimizi icra edecek olursak (yani kendi mesleğimiz doğrultusunda bir iş sahibi olursak) Evrim Ağacı'na zaman ayıramayacağımızı, ayakta tutamayacağımızı biliyoruz. Çünkü az sonra detaylarını vereceğimiz üzere, Evrim Ağacı sosyal medyada denk geldiğiniz makale ve videolardan çok daha büyük, kapsamlı ve aşırı zaman alan bir bilim platformu projesi. Bu nedenle bizler, meslek olarak Evrim Ağacı'nı seçtik.

Eğer hem Evrim Ağacı'ndan hayatımızı idame ettirecek, mesleklerimizi bırakmayı en azından kısmen meşrulaştıracak ve mantıklı kılacak kadar bir gelir kaynağı elde edemezsek, mecburen Evrim Ağacı'nı bırakıp, kendi mesleklerimize döneceğiz. Ama bunu istemiyoruz ve bu nedenle didiniyoruz.

Destek Ol

1. Oyuncular
2. Aksiyonlar
3. Kazançlar

idi. Fark ettiyseniz, bu ögelerin içinde “kurallar” ya da onun yerine geçebilecek bir şey mevcut değil. Bunun sebebi, oyunlarda “kurallar” olarak bilinen şeylerin, aslında oyuncuların aksiyonlarını (yani aksiyon kümelerinin çarpımını) belirli kazanç değerlerine eşleyen kazanç fonksiyonunun içine gömülü olmasıdır. Sözgelimi, iki oyunculu bir oyunda, kural, her oyuncunun kendisinin seçtiği 1 ile 9 arasında bir rakam ile öteki oyuncunun seçtiği 1 ile 9 arasındaki rakamın farkı kadar para kazanacağı yönünde olsun. Bu durumda, Oyuncu 1 r₁ ve Oyuncu 2 r₂ rakamlarını seçmişse, Oyuncu 1’in kazanç fonksiyonu

u₁(r₁,r₂) = r₁-r₂

olarak tanımlanabilir. Bu da, oyunun “kuralını” kendi içinde barındıran bir fonksiyondur. Bunu akılda canlandırmanın bir diğer yolu, kazanç fonksiyonunu içerisinde oyunun kurallarını barındıran bir kara kutu olarak yorumlamak olabilir.

“Kazanç Fonksiyonu” olarak belirtilen kara kutu, oyunun tüm kurallarını (mutlak kurallar, şans faktörleri, vb.) içinde barındırmaktadır. Bu sebeple, aslında oyuncunun oyunun kurallarının ne olduğunu bilmediği durumlar, kazanç fonksiyonunun ne olduğunu bilmediği durumlardır. Bunlar da, kazanç fonksiyonumuzu ya da onun çıktıları olan kazanç değerlerimizi değiştirerek modellenebilir.

Eğer Bayes oyunlarının arkasındaki temel anlayış aklınıza yattıysa, biraz da bu oyunların teorisine bakalım.

Bayes Oyunlarının Tanımları

Bayes oyunları için birbirine eşdeğer iki tanım kullanılmaktadır. İlk başta karmaşık gelebilecek bu tanımların, ilerleyen paragraflarda, örneklerle açıklığa kavuşacağını umuyoruz.

Birinci Tanım: Bayes oyunları, tek farkları kazanç değerleri olan (yani oyuncuların ve oyuncuların seçebileceği aksiyonların aynı olduğu) ve oyuncuların hangi oyunu oynadıklarına yönelik inançları / önyargıları (bilgi setleri) olan bir oyunlar kümesidir. Bu tanım, şu ana kadar kullandığımız klasik tanımdır. Bu tanımda bilgi setleri olarak tanımlanan fonksiyon, sadece hangi oyuncunun hangi oyunu oynadığına ne kadar ihtimal verdiği yönündeki bilgileri içeren bir fonksiyondur ve şu ana kadar bahsettiklerimizden bir farkı yoktur.

İkinci Tanım: Bayes oyunları, normal formda oyunları tanımlamak için kullanılan “oyuncular,” “aksiyonlar” kümeleri ve “kazanç fonksiyonu”nun yanı sıra, “tipler” kümesi ve “önyargılar (inançlar) fonksiyonu”nu içeren bir demettir. Burada bahsedilen

• Tipler kümesi, her oyuncunun alabileceği tipleri içerir.
• Önyargılar kümesi, bir oyuncunun, kendisinden başka her oyuncunun muhtemel her tipi için sahip olduğu (hangi oyuncunun hangi tipe sahip olduğu konusundaki) önyargıları ya da inançları ifade eder.

Bu iki tanımın arasında pratikte hiçbir fark yoktur. Sadece, iki farklı anlayışı ifade etmektedirler ve farklı Bayes oyunlarında farklı birini kullanmak daha anlamlı olabilir. Sözgelimi, bilgi setleri ve birden fazla sayıda oyun üzerinden giden birinci tanım, “Var Mısın Yok Musun?” gibi şans oyunlarında, ya da belirsizliğin oyunun yapısından kaynaklandığı benzeri durumlarda anlamlı olacaktır. Tipler üzerinden açıklanan ikinci tanım ise, açık artırmalar, yukarıda bahsedilen yeni arkadaş grubunda politik görüş bildirme durumu ya da başkanlık seçimleri gibi, oyundaki (kazançlardaki) belirsizliğin diğer oyuncuların tercihlerini ve düşüncelerini bilmemekten kaynaklandığı durumlara daha iyi uymaktadır. Bu iki tanım arasındaki tek fark, belirsizliği hangi faktörün üzerine yükleyeceğimizdir.

Oldukça soyut bir örnek üzerinden, bu iki tanımın ne anlama geldiğini kavradıktan sonra, daha gerçekçi bir örnekte de neden bu ikisinin eşdeğer olduğunu, ve bir Bayes oyununun nasıl analiz edilebileceğini görelim.

Örnek: Ortaya Karışık Oyunu

Elbette ki gerçek hayatta bir insan, o an yazı-tura mı attığını, yoksa polisler tarafından sorguya mı çekildiğini; araba mı kullandığını, yoksa sevgilisiyle buluşmaya çalıştığını mı biliyor olacaktır. Ancak biz bu gerçeği hiç kafamıza takmadan, tanıdık oyunlar üzerinden soyut örneğimizi verelim: Öyle bir Bayes oyunu düşünün ki, iki oyuncu, Tutsak İkilemi, Cinsiyetlerin Savaşı, Para Eşleme ve Karşılaşan Arabalar oyunlarından birini oynuyor olsunlar, ancak hangisini oynadıklarını bilmesinler. Her oyunda Oyuncu 1 ya “yukarı” (Y) ya da “aşağı” (A) hamlesini seçebilirken, Oyuncu 2 ya “sol” (<) ya da “sağ” (>) hamlesini seçebilsin. Bu Bayes oyununu şu şekilde ifade edebiliriz:

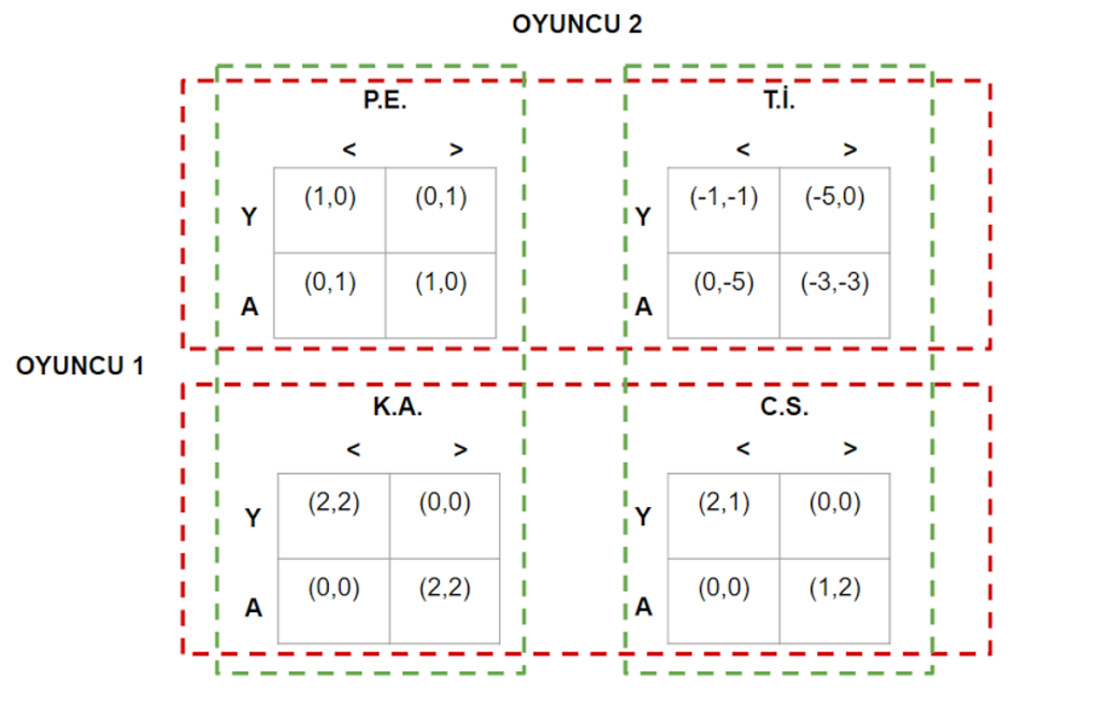
Bu gösterimde, kırmızı kesik çizgilerle gösterilen iki küme, Oyuncu 1’in bilgi setleri ya da tipleridir. Benzer şekilde, yeşil kesik çizgilerle gösterilen iki küme de Oyuncu 2’nin bilgi setleri ya da tipleridir. Bu demektir ki, Oyuncu 1 ya Para Eşleme ya da Tutsak İkilemi’ni; veya ya Karşılaşan Arabalar ya da Cinsiyetlerin Savaşı’nı oynadığını bilmektedir. Benzer şekilde, Oyuncu 2 de, ya Para Eşleme ya da Karşılaşan Arabalar’ı; veya ya Tutsak İkilemi ya da Cinsiyetlerin Savaşı’nı oynadığını bilmektedir. Örneğin, eğer gerçekten oynanan oyun Tutsak İkilemi ise, Oyuncu 1 Para Eşleme mi Tutsak İkilemi mi oynadığını bilmeyecek, ancak Karşılaşan Arabalar ya da Cinsiyetlerin Savaşı oynamadığından yüzde yüz emin olacaktır. Oyuncu 2 de Tutsak İkilemi mi Cinsiyetlerin Savaşı oyunlarının arasında kararsız kalacaktır, gibi.

Şu ana kadar bu oyuna ilk tanımın gözüyle baktık. Ama aynı şekilde, tipler olarak da bakabiliriz: Örneğin, Tutsak İkilemi oynanıyorsa Oyuncu 1, üstteki kümeye, yani Tip1 1’e aittir. Eğer Cinsiyetlerin Savaşı oynanıyorsa alttakine, Tip1 2’ye aittir, vb. Oyuncu 1, eğer Tip1 1’e aitse Tutsak İkilemi ve Para Eşleme arasında kalacaktır. Hangisini oynadığı yönündeki tahmini, tamamen Oyuncu 2’nin tipi yönündeki tahminine bağlıdır, zira bu iki tipin kesişimi aslında oynanan oyunu ifade etmektedir. Eğer Oyuncu 1, Oyuncu 2’nin Tip2 2’ye ait olduğuna %90 ihtimal veriyorsa, iki tipin kesişimi Para Eşleme olacağı için, %90 ihtimalle Para Eşleme oynadığını düşünecek ve hamlesini ona göre yapacaktır.

Agora Bilim Pazarı

Büyük Sanatçıların Gizli Hayatları

Leonardo’dan (sözde sodomist) tutun da Caravaggio’ya (hüküm yemiş katil), Edward Hopper’a (karısını dövmekle itham edilir) varana kadar herkes hakkında taşkın anekdotlar sunan Büyük Sanatçıların Gizli Hayatları, büyük ustaların uluslararası sanatının gerisindeki ahlâksızca, buğulu ve gözü kara hikâyeleri anlatıyor. Michelangelo’nun vücut kokusu çok kötü olduğu için asistanlarının onunla çalışmaya dayanamadığını; Vincent van Gogh’un bazen doğrudan doğruya tüpten boya yediğini; ve Georgia O’Keefe’nin çıplak resim yapmaya bayıldığını öğreneceksiniz. İşte asla unutmayacağınız bir sanat tarihi dersi.
Öğretmenlerinizin Size Büyük Ressamlar ve Heykeltraşlar Hakkında Asla Anlatmadığı Şeyler
ELIZABETH LUNDAY mimari ve sanat konusunda uzman olan bir gazeteci. mental_floss dergisinin “Şaheserler” sütununu yazıyor.
CİNAYET, SAHTEKÂRLIK, DÜZENBAZLIK VE BÜYÜK SANAT ÜZERİNE GERÇEK HİKÂYELER….

Devamını Göster

₺210.00

Satın Al Tüm Ürünler

• Dış Sitelerde Paylaş

Görüldüğü üzere, iki tanım arasında hiçbir fark yoktur. Sadece, farklı açılardan (oyuncu veya oyun) bakmak için kullanılmaktadırlar. Bazen matematiksel analizlerde de, bir tanımın diğerine üstünlüğü olmakla birlikte, bizim kalacağımız seviyede bunlardan bahsetmenin gereği yoktur.

Örnek: Şerif ve Suçlu

Sonunda, daha anlamlı bir Bayes oyununu detaylıca inceleyebileceğiz.

Bu oyunun ismi, Şerif ve Suçlu. Bir vahşi batı bağlamındayız. kasabamızın devriye gezen şerifi var. Şerif, devriyesinde, silahlı bir adama rast geliyor. Bu iki adam, aynı anda birbirlerini vurup vurmamaya karar vermek zorundalar. (Western filmlerindeki ikonik “aynı anda silah çekme” sahnelerini hatırlayın.) Ancak, şerif bu silahlı adamın bir suçlu mu, yoksa bir masum mu olduğunu bilmiyor; “p” ihtimalle masum olduğunu düşünüyor. (p, şerifin inancını temsil eden bir değişken.) Kazançlar ise şu şekilde:

• Şerif, eğer şüpheli kendisini vuracak olursa vurmayı, şüpheli kendisini vurmaya yeltenmezse de vurmamayı tercih eder. Nitekim, şerifimiz bir kanun adamı ve ne olursa olsun hayatına kast etmeyen birisini öldürmek istemez.
• Silahlı adam suçlu ise, her durumda vurmayı tercih eder, zira şerif kendisini vurmasa bile, suçlu olduğunu anladığı anda kodese gidecektir.
• Silahlı adam eğer masum ise, şerif kendisini vursa da vurmasa da kendisi şerifi vurmak istemeyecektir. Bunun da sebebi, adamın yüksek ahlaki erdemlere bağlı olması, veya bir şerifi öldüren kişi olarak hatırlanmak istememesi olabilir.

Tabii ki, hamleler aynı anda yapılacağı için oyun kızgınlaşıyor. Şerifin gözünden bakıldığında, ortada kazançları tamamen değiştiren iki ihtimal var: Silahlı adam masum mu, suçlu mu? Bu durumu bir Bayes oyunu olarak ifade edersek:

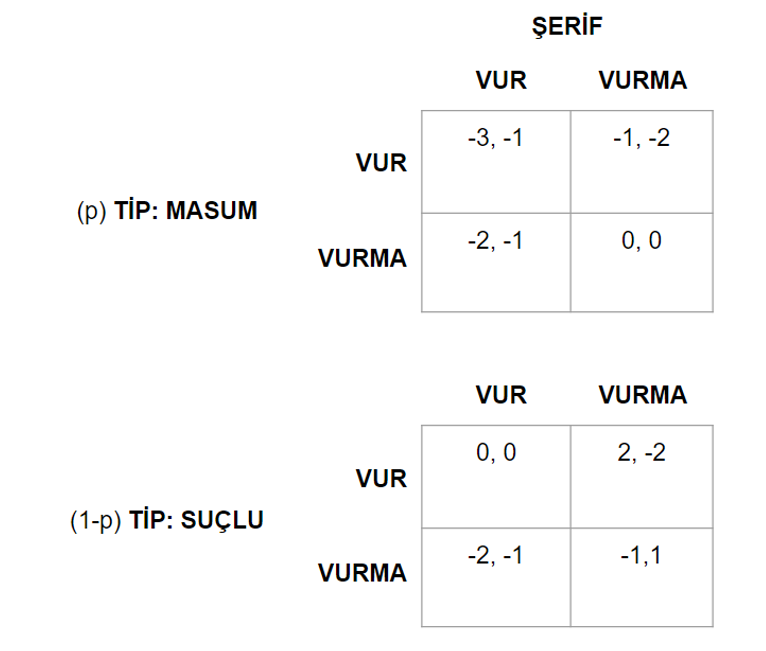
Burada, Oyuncu 1’in (silahlı adam) hangi tipte olduğuna göre, şerifin oynadığı oyun değişebiliyor. Şerifin, diğer oyuncunun tipine yönelik belli bir inancı var. Şimdi, şerifin inancının ne yönde olduğuna göre (yani p’nin değerine göre) şerifin yapması “gereken” hamleyi analiz edelim.

Zaten yukarıda da belirttiğimiz gibi, suçlu daima vurmayı, masum da daima vurmamayı tercih etmektedir. Bunu, kazanç değerlerinden de görebiliriz: Şerif vursa da, vurmasa da suçlu vurursa, masum da vurmazsa daha fazla kazanç elde edebilecektir. Bir başka deyişle, vurmak suçlunun, vurmamak da masumun baskın stratejisidir. Bu yüzden, oyunu şöyle sadeleştirebiliriz:

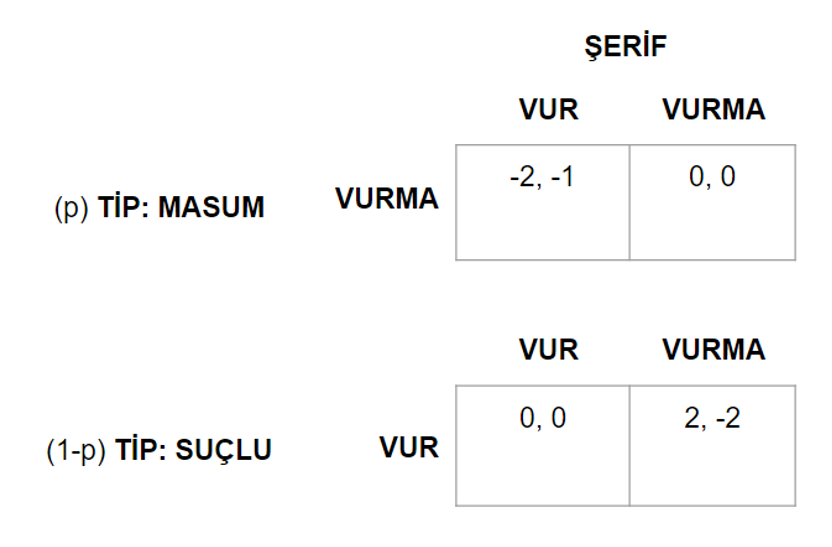
Şimdi kolaylıkla, şerifin vurması ve vurmaması durumlarında elde edeceği kazanç beklentilerine bakabiliriz.

1. Şerif vurursa, p olasılıkla -1, 1-p olasılıkla da 0 kazanca sahip olacaktır. Buna göre, KB_Ş,VUR = -p + 0*(1-p) = -p
2. Şerif vurmazsa, p olasılıkla 0, 1-p olasılıkla da -2 kazanacaktır. Yani, KB_Ş,VURMA = 2p - 2

Şerifin vurmamayı tercih etmesi için, gerekli şart:

 KB_Ş,VURMA > KB_Ş,VUR

2p - 2 > -p

3p > 2

p > ⅔

Bir başka deyişle, eğer şerif karşısındaki silahlı adamın masum olmasına ⅔’ten (%67’den) daha fazla ihtimal veriyorsa, vurmamayı tercih etmelidir.

Mekanizmalar: Açık Artırmalar, Seçim Sistemleri, vb.

Bayes oyunları basit, ama uygulaması ve detayı çok fazla olan bir alandır. Mekanizmalar ve İdeal Mekanizmaların Tasarımı ise, bunlar arasında en popüler olanlarından biridir. Mekanizma Tasarımı’nı etraflıca anlatmak, başlı başına bir yazı dizisi alacaktır ve o dizinin makaleleri takip edebilmek için çok ileri düzey bir matematik gerektirecektir. Coursera’da Stanford Üniversitesi tarafından verilen iki derslik Oyun Teorisi serisinin ikinci dersinin neredeyse tamamen Mekanizma Tasarımı konusuna ayrılmış olması, zannediyoruz ki konunun genişliğini aklınızda canlandırmanıza yardımcı olacaktır. İleride Mekanizma Tasarımı’ndan bu sayfalarda bahseder miyiz bilinmez ama, konuyu Bayes oyunları başlığı altında çok kısaca tartışmanın yerinde olacağını düşündük.

Mekanizma dediğimiz şey, aslında yukarıda “Neden kurallar değişmiyor?” sorusuna cevap verirken kullandığımız “kara kutu”dan ibaret. Yani, bir Bayes oyunu bağlamını (bir başka deyişle, oyuncular, aksiyonlar ve muhtemel sonuçlardan oluşan küme) bir oyuna dönüştüren eksik parça. Yukarıdaki görseli, şu şekilde modifiye edebiliriz:

Oyuncular, stratejilerini belirleyerek aksiyonlarını seçerler. Tüm oyuncuların aksiyonları, mekanizma tarafından toplanır ve mekanizmanın yapısına göre, bir sonuç doğurur. Oyuncuların kazançları da, bu sonucun içindedir. Aynı oyuncuların aynı aksiyonları seçtiği bir durum, farklı mekanizmalarda farklı sonuçlara sebebiyet verebilir.

Aklımıza gelebilecek pek çok mekanizma olmakla birlikte, bunlardan en popülerleri açık artırmalar ve seçim sistemleridir. İkisi de, pek çok oyuncudan fikirlerini bildirmelerini ister (ürüne vermeye razı oldukları fiyat, ya da adayları tercih sırasına koymaları, vb.) ve bunları bir sonuca götürür. (Kazanan adayı belirleme, ürünün satılacağı kişiyi ve satış fiyatını belirleme, vb.)

Bu mekanizmaların tasarımı, alanın başlıca ilgi alanlarındandır. Yani, bir nevi oyunun “kurallarını” öyle bir şekilde manipüle edeceğiz ki, ortaya bizim kriterlerimize mümkün olduğunca uygun sonuçlar çıkacak. Sözgelimi, demokratik bir seçim sistemi tasarlıyorsak, bu sistemin hem çoğunluğun iradesine dayalı olmasını (yani, belirli bir kişinin ya da grubun sözünün diğerlerinkinden daha geçerli olmamasını, diktatöryel olmamasını) hem de adayların gerçek tercihlerini doğru bir şekilde yansıtacakları şekilde kuralları olmasını isteriz. Örnek olarak, 2015 Haziran’ında Türkiye’de yapılan genel seçimlerdeki tanıdık bir duruma bakabiliriz. Hepimizin çok iyi bildiği gibi, bu seçimlerde A partisinin seçmenlerinin bir kısmı, B partisinin barajı aşıp meclise girebilmesi için, normalde A partisini B partisine tercih edecek olmalarına rağmen B partisine oy vermişlerdi. Bunun sebebi de, B partisi barajı aşıp meclise girerse, A partisi seçmeninin bir kısmının tercih sırasında B’nin de altına koyduğu C partisinin kazanacağı koltuk sayısının dramatik bir şekilde azalacak olmasıydı. Nitekim, o kısmın büyük çoğunluğu bu sebeple gerçek tercihlerini (A) değil, istedikleri sonuca ulaşmalarını sağlayacak olan partiyi (C) oylamışlardır. Bu, mekanizmanın seçmenlerin isteklerini tam olarak yansıtmamalarının kendilerinin karına olmasına sebebiyet veren bir yapının göstergesidir. Bir başka deyişle, bu “2015 Seçimleri” oyununun Nash dengesi, tüm seçmenlerin gerçek tercihlerini yansıtması değil, A’yı B’ye tercih etmelerine rağmen B’yi de C’ye tercih edenlerin B’ye oy vermesidir.

Açık artırma mekanizmalarının tasarımında ise, yine alıcıların ürüne gerçekten biçtikleri fiyatı söylemeleri, eğer fiyat hem alıcının vermeye razı olduğundan düşükse ve satıcının almaya razı olduğundan fazlaysa satışın yapılması, veya satıcının mümkün olan maksimum kara sahip olması kriterleri göz önünde bulundurulabilir.

Sonuç

Bayes oyunlarının tanımından ortaya çıkan bir kavram olan Mekanizmalar’dan, yeniden Bayes oyunlarına dönecek olursak, bu konudaki tartışmamızı, Bayes oyunlarının gerçek hayattaki pek çok duruma tekabül etmekte olduğunu söyleyerek bitirebiliriz. Kendimizi içinde bulduğumuz her durum, bir oyun olarak modellenebileceği gibi, bu oyunların hemen hepsi de aslında birer Bayes oyunundan başka bir şey değildir. Sizin, vereceğiniz kararların sonuçlarını, onlardan size dönecek kazancı, veya diğer oyuncuların değerlerini kesin olarak bildiğiniz modeller, sadece birer varsayımdır, analizleri basitleştiren bir idealizasyondur. Bu idealleştirme, birçok durumda uygulanabilir, zira oyunu oldukça basitleştirmekle birlikte, fazla bir hata payına sahip değildir. Sözgelimi, Cinsiyetlerin Savaşı’nı düşünürsek, pek çok çiftin operayı veya sinemayı, sevgililerini ekmeye değecek kadar sevmediğini söylemek hatalı bir varsayım olmayacaktır. Ancak şerif/suçlu oyununda olduğu gibi daha karmaşık durumlarda, artık Bayes oyunu modeline geçmemiz gerekir, çünkü iki durum arasında varsayım yapamayacağımız kadar büyük bir fark vardır.

En başta bahsettiğimiz gibi, bunu bir fizik problemine benzetebiliriz. Eğer, yerden 10 metre yüksekten bıraktığımız bir topun hareketini inceliyorsak, yerçekimini sabit almamız, hesaplarımızı çok fazla değiştirmeyecektir. Çünkü topun yer değiştirmesi (10 metre) yerçekimi kuvvetini etkileyen değişken faktör olan Dünya’nın yarıçapından (yaklaşık 13 bin kilometre) ihmal edilebilir derecede küçüktür. Ancak aynı topu 10 metre yüksekten değil de, yerden 10 bin kilometre yüksekten, ekzosferden bırakacak olursak, artık yerçekimi kuvvetinin değişken olduğunu hesaba katmamız gerekir. 10 bin kilometre, 13 bin kilometreye kıyasla ihmal edilebilir bir rakam değildir.

Bayes oyunlarından sonra bakacağımız oyun türü, tekrar eden oyunlar olacaktır. Aynı Bayes oyunları gibi pek çok duruma uyarlanabilecek olan bu çeşidi incelerken, aynı zamanda Tutsak İkilemi’ni “çözerek” 2. yazımızda sorduğumuz bir sorunun cevabını vereceğiz.