Riemann İntegrali Nedir? Ne İşe Yarar?

Riemann integrali, ilk olarak Bernhard Riemann tarafından oluşturulan, tanımlı bir aralık üzerindeki bir fonksiyonun integralinin ilk geçerli tanımıdır. Bu tanım 1854 yılında Göttingen Üniversitesi öğretim üyelerine sunulmuş, ancak ilk defa 1868 yılında bir dergide yayınlanmıştır. Birçok fonksiyon ve pratik uygulama için Riemann integrali, kalkülüsün temel teoremi ile birlikte değerlendirilebilir. Sayısal integrasyon ile yaklaşık olarak hesaplanabilir veya Monte Carlo integrasyonu kullanılarak simüle edilebilir.^[1]

Riemann İntegrali Nasıl Hesaplanır?

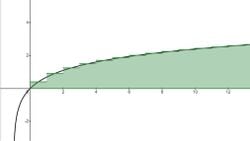
Bir dikdörtgenin alanını herkes hesaplayabilir. Karşılıklı olmayan 2 kenarın çarpımını alarak alanı bulabilirsiniz. Üçgen içinse taban ile yüksekliği çarpıp ikiye bölmek yeterlidir. Diğer düzgün çokgenlerin alanlarını da benzer şekilde hesaplayabilirsiniz. Peki aşağıdaki gibi bir şeklin alanı nasıl hesaplanır?

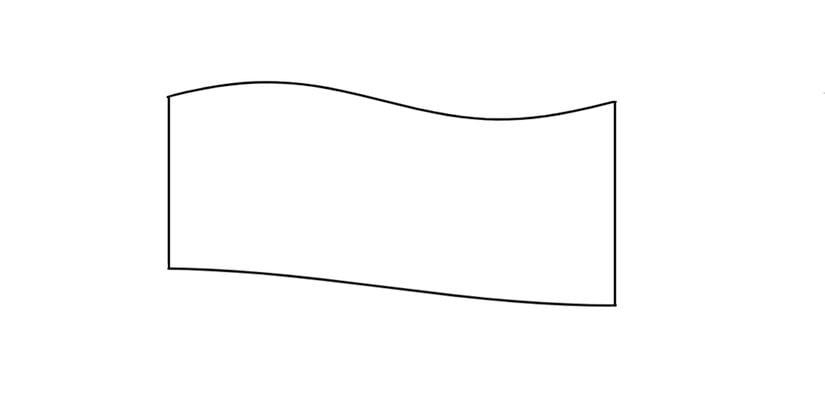
Aslında bu alanı yaklaşık olarak bulmak mümkün. Şeklin alanı $S$ olsun. Şeklin içinde kalan bir dikdörtgen çizelim:

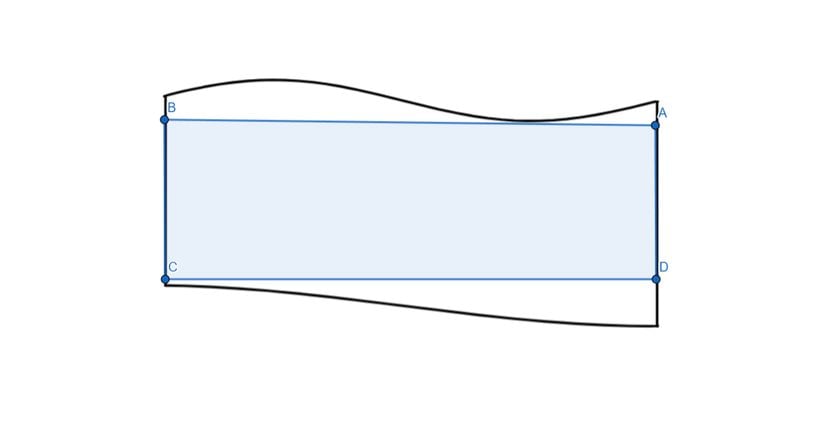
Bu dikdörtgenin alanına $A$ diyelim. Bir de alanı kapsayan bir dikdörtgen çizelim:

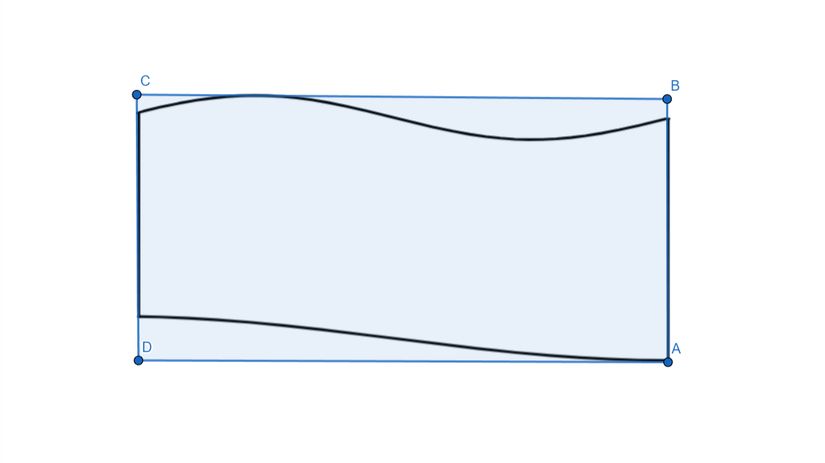
Bu dikdörtgenin alanına da $B$ diyelim. Şimdi şunu söyleyebiliriz: $S$, $A$'dan büyük $B$'den küçüktür. Yani $|A|<|S|<|B|$ denebilir, fakat bu $S$'nin değer aralığını yeterince daraltmadığı için ideal değil. Daha yakın değerler elde etmek ve aralığı daraltmak için ilk şekli şöyle düzenleyelim:

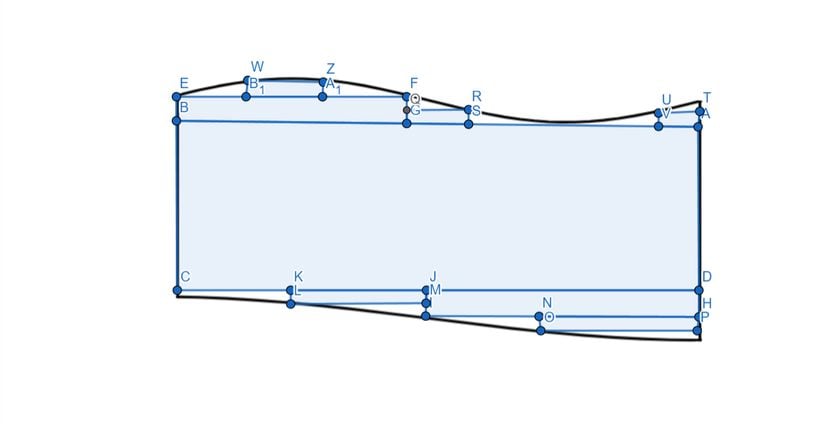
Bu şekilde, ilk denememizden daha fazla dikdörtgen kullandık. Böylece gerçek alana daha fazla yaklaştık. Şimdi diğeri için de benzer bir şey yapalım. Bu sefer kenarlara yaklaşacağız:

Şimdi aralığımız daha çok daraldı. Yani elimizdeki dikdörtgenlerin alanları toplamı $S$'ye daha yakın ama eşit değil. İşte $A$ ve $B$ değerleri birbirlerine yaklaşırsa ve sonunda $|A|=|B|$ olursa $S$ alanına ulaşılır, çünkü $S$ de bu iki alana eşit olmalıdır. Bu noktada $A$ için en büyük alt sınır, $B$ için en küçük üst sınır deriz. İşte Riemann integrali bunu fonksiyonlar için kullanarak fonksiyonların altında kalan alanı hesaplar. O zaman fonksiyonlarda bunu uygulamaya geçelim.

Öncelikle bir $[a,b]$ aralığında pozitif ve tanımlı bir $f(x)$ fonksiyonu alalım. Şimdilik bu fonksiyonu $[a,b]$ aralığında pozitif kabul edelim. Şimdi de bu $[a,b]$ aralığına bir göz atalım.

Şimdi bu doğru üstünden $a=x_0<x_1<x_2<\cdots <x_i<\cdots <x_n=b$ özelliklerini sağlayan $x$ noktaları alalım. Şimdi bir $P$ kümesi oluşturalım ve şu şekilde tanımlayalım:

$P=\{x_0,x_1,x_2,\dots x_i,\dots ,x_n\}$

Bu $P$ kümesine $[a,b]$ aralığının parçalanması veya bölüntüsü denir. Şimdi aşağıdaki özelliği sağlayan bir $\Delta x_i$ tanımlayalım:

Evrim Ağacı'ndan Mesaj

Neden Desteğe İhtiyacımız Var?

Aslında maddi destek istememizin nedeni çok basit: Çünkü Evrim Ağacı, bizim tek mesleğimiz, tek gelir kaynağımız. Birçoklarının aksine bizler, sosyal medyada gördüğünüz makale ve videolarımızı hobi olarak, mesleğimizden arta kalan zamanlarda yapmıyoruz. Dolayısıyla bu işi sürdürebilmek için gelir elde etmemiz gerekiyor.

Bunda elbette ki hiçbir sakınca yok; kimin, ne şartlar altında yayın yapmayı seçtiği büyük oranda bir tercih meselesi. Ne var ki biz, eğer ana mesleklerimizi icra edecek olursak (yani kendi mesleğimiz doğrultusunda bir iş sahibi olursak) Evrim Ağacı'na zaman ayıramayacağımızı, ayakta tutamayacağımızı biliyoruz. Çünkü az sonra detaylarını vereceğimiz üzere, Evrim Ağacı sosyal medyada denk geldiğiniz makale ve videolardan çok daha büyük, kapsamlı ve aşırı zaman alan bir bilim platformu projesi. Bu nedenle bizler, meslek olarak Evrim Ağacı'nı seçtik.

Eğer hem Evrim Ağacı'ndan hayatımızı idame ettirecek, mesleklerimizi bırakmayı en azından kısmen meşrulaştıracak ve mantıklı kılacak kadar bir gelir kaynağı elde edemezsek, mecburen Evrim Ağacı'nı bırakıp, kendi mesleklerimize döneceğiz. Ama bunu istemiyoruz ve bu nedenle didiniyoruz.

Destek Ol

$\Delta x_i=x_i-x_{i-1}$

Bu durumda $[a,b]$ aralığının da uzunluğu $b-a$ olur ve bu da şu eşitliği sağlar:

$[a,b]=b-a=\Delta x_1+\Delta x_2+\Delta x_3+\cdots +\Delta x_i+\cdots +\Delta x_n$

Bu aralıklardan en büyüğüne $P$ bölüntüsünün normu denir ve genelde $||P||$ olarak gösterilir. Eğer en büyük aralığa eşit birden fazla aralık varsa hepsi norm kabul edilir.^{[4], [3], [2]}

Şimdi hesaplamaya geçelim. $P=\{x_0,x_1,x_2,\dots x_i,\dots ,x_n\}$ kümesi de $[a,b]$'nin bölüntüsü olsun. Her $\Delta x_i$ için $m_i$ en büyük alt sınır, $M_i$ ise en küçük üst sınır olsun. Ayrıca $t_i\in \Delta x_i$ olsun, böylece şunu söyleyebiliriz:

$m_i<f(k_i)<M_i$

Şimdi eşitliğin her tarafını $\Delta x_i$ ile çarpalım. Bu eşitliği bozmaz: $\Delta x_i$ her zaman pozitiftir, çünkü uzunluk ifade eder:

$\Delta x_i\cdot m_i<\Delta x_i\cdot f(k_i)<\Delta x_i\cdot M_i$

Şimdi de bunların $i$'ye göre toplamını alalım:

$\sum _{i=1}^n\Delta x_i\cdot m_i<\sum _{i=1}^n\Delta x_i\cdot f(k_i)<\sum _{i=1}^n\Delta x_i\cdot M_i$

Biraz da bu formüllerin geometrik anlamlarına göz atalım. Önce $\sum _{i=1}^n\Delta x_i\cdot m_i$ için bakalım.

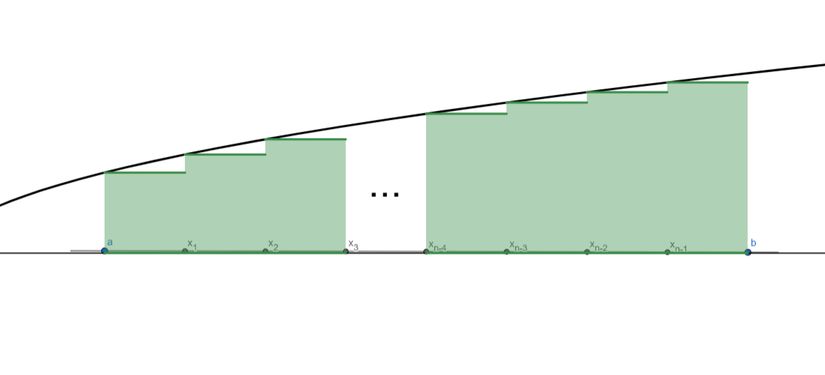
Buradaki $n$ tane sütunun alanları toplamı bize alt sınırı verir. Genelde bunu $A(f,P)$ olarak gösteririz. Anlaşılacağı üzere $P$ kümesinin ne kadar çok elemanı olursa alt sınır gerçek alana o kadar yaklaşır. Şimdi üst sınıra yani $\sum _{i=1}^n\Delta \cdot x_i{M}_i$ bakalım.

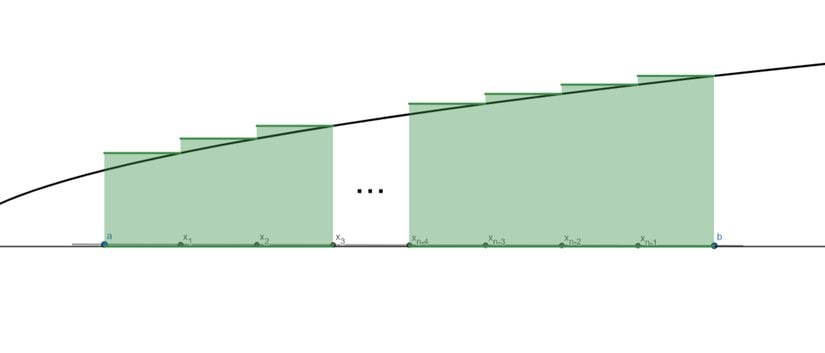
Bunu da $\ddot{U}(f,P)$ şeklinde gösteririz, bu da üst toplam olur. Bunda da kutucuk sayısı ne kadar artarsa gerçek alana o kadar yaklaşılır. Peki gerçek alan nasıl bulunur? Bu dikdörtgenlerin sayısını sonsuza yaklaştırarak tabii ki. Ama sadece sonsuza yaklaştırmak yetmez. Aynı zamanda $\Delta x_i$'leri de $0$'a yaklaştırmamız gerekir. Bunu şu şekilde gösterelim:

Agora Bilim Pazarı

8.SINIF ULTRA KAZANIM KAVRAMA DENEMELERİ 68 FASİKÜL TÜM DERSLER

Devamını Göster

₺915.00

Satın Al Tüm Ürünler

• Dış Sitelerde Paylaş

$\underset{||P||\to 0}{\lim }A(f,P)\le \underset{||P||\to 0}{\lim }R(f,P)\le \underset{||P||\to 0}{\lim }\ddot{U}(f,P)$

Buradaki $R(f,P)$ gerçek alan anlamındadır. Bunu az önceki $\sum _{i=1}^n\Delta x_i\cdot f(k_i)$ ile karıştırmayın, çünkü bu size gerçek alanı vermez.

Az önceki eşitsizlikte limit $0$'a gittikçe $A(f,P)$ ve $\ddot{U}(f,P)$ birbirine yaklaşacaktır. Eğer aşağıdaki sonuca ulaşılırsa Sandviç teoremi gereğince artık gerçek alanı yani $R(f,P)$'i bulmuş oluruz:

$\underset{||P||\to 0}{\lim }A(f,P)=\underset{||P||\to 0}{\lim }\ddot{U}(f,P)$

İşte buna Riemann integrali deriz. Riemann ise bunu şöyle göstermiştir:

$\underset{||P||\to 0}{\lim }R(f,P)=\underset{||P||\to 0}{\lim }[\sum _{i=1}^n\Delta x_i\cdot f(k_i)]={\int }_a^{b}f(x)dx$

Gelin $||P||$'yi $0$'a götürmek yerine bütün aralıkları eşit varsayalım. Yani her $\Delta x_i$ eşit olsun. Şimdi aralık sayısını, yani $n$'ni sonsuza götürelim:

$\underset{n\to \infty }{\lim }[\sum _{i=1}^n\Delta x_i\cdot f(k_i)]={\int }_a^{b}f(x)dx$

İşte bu şekilde bir fonksiyonun grafiğinin altında kalan alanı hesaplayabilirsiniz.^{[7], [6], [5], [4]}

İntegralden Riemann Toplamı Bulmak

Gelin aşağıdaki integralden Riemann toplamını bulalım:

${\int }_0^4{x}^{2}dx$

Öncelikle bu aralığın uzunluğunu bulalım. $4-0$'dan $4$ gelir. Aralığı $n$ eşit parçaya bölelim. Her bir parçanın uzunluğu $\frac{4}{n}=\Delta x_i$ olur. Şimdi $t_i$'yi bulmak için şu formülü uygulayalım:

$t_i=a+i\cdot \Delta x_i$

Burada $a=0$ ve ve $\Delta x_i=\frac{4}{n}$ olduğu için $t_i=0+i\cdot \frac{3}{n}$ olur. Bulduklarımızı yerine koyalım:

$\underset{n\to \infty }{\lim }[\sum _{i=1}^n\Delta x_i\cdot f(k_i)]={\int }_a^{b}f(x)dx$

$\underset{n\to \infty }{\lim }[\sum _{i=1}^n\frac{4}{n}\cdot (i\cdot \frac{4}{n}{)}^2]={\int }_0^4{x}^{2}dx$

Şimdi ilk toplamı hesaplayalım. Bunun için parantezden kurtulalım:

$\underset{n\to \infty }{\lim }[\sum _{i=1}^n\frac{4}{n}\cdot (i\cdot \frac{4}{n}{)}^2]$

$\underset{n\to \infty }{\lim }[\sum _{i=1}^n\frac{4}{n}\cdot (i^2\cdot \frac{4^2}{n^2}\left)\right]$

$\underset{n\to \infty }{\lim }\left[\sum _{i=1}^n\frac{4^3\cdot i^2}{n^3}\right]$

Şimdi $\frac{4^3}{n^3}$ kısmını dışarı alalım:

$\underset{n\to \infty }{\lim }\frac{4^3}{n^3}\left[\sum _{i=1}^n{i}^2\right]$

Kareler toplamı (İng: "Sum of Squares") formülünü uygulayalım:

$\underset{n\to \infty }{\lim }\frac{4^3}{n^3}\cdot \frac{n(n+1)(2n+1)}{6}$

Sadeleştirelim:

$\underset{n\to \infty }{\lim }\frac{32(n+1)(2n+1)}{3n^2}$

$\underset{n\to \infty }{\lim }\frac{64n^2+96n+32}{3n^2}$

İfadeyi şöyle yazalım:

$\underset{n\to \infty }{\lim }\frac{64n^2}{3n^2}+\frac{96n}{3n^2}+\frac{32}{3n^2}$

Sadeleştirmeleri yapalım:

$\underset{n\to \infty }{\lim }\frac{64}{3}+\frac{32}{n}+\frac{32}{3n^2}$

Paydalarında $n$ olanlar limitte $0$'a yaklaştığı için $0$ olurlar. Bu yüzden sadece $\frac{64}{3}$ kalır ve cevabımız $\frac{64}{3}$ olur.

Riemann Toplamından İntegrali Bulmak

Aşağıdaki ifadeyi ele alalım:

$\underset{n\to \infty }{\lim }\left(\frac{1^9+2^9+3^9+4^9+\cdots +n^9}{n^{10}}\right)$

Önce $\frac{1}{n}$'i dışarı alalım:

$\underset{n\to \infty }{\lim }\left(\frac{1}{n}\right)\left(\frac{1^9+2^9+3^9+4^9+\cdots +n^9}{n^9}\right)$

Bölümü toplam olarak ayıralım:

$\underset{n\to \infty }{\lim }\left(\frac{1}{n}\right)(\frac{1^9}{n^9}+\frac{2^9}{n^9}+\frac{3^9}{n^9}+\cdots +\frac{n^9}{n^9})$

Hepsini toplam olarak yazalım:

$\underset{n\to \infty }{\lim }\left(\frac{1}{n}\right)\left[\sum _{i=1}^n\right(\frac{i}{n}{)}^9]$

Şimdi $\frac{1}{n}$ kısmını içeri alalım.

$\underset{n\to \infty }{\lim }\left[\sum _{i=1}^n\right(\frac{1}{n}\left)\right(\frac{i}{n}{)}^9]$

Şimdi bu toplama bakalım. $\frac{1}{n}$ aralığımız yani $\Delta x_i$'miz. $(\frac{i}{n}{)}^9$ise $a+i\Delta x_i$. $\Delta x_i$'nin $\frac{1}{n}$ olduğunu biliyoruz. Yani $a=0$ oldu. $\frac{b-a}{n}=\frac{1}{n}$ yani $b=1$.$f(\frac{i}{n})=(\frac{i}{n}{)}^9$ yani $f(x)=x^9$ gelir. O zaman integralimiz bu olmalı:

${\int }_0^1{x}^{9}dx$

Yani sonuç budur:

$\underset{n\to \infty }{\lim }\left(\frac{1^9+2^9+3^9+4^9+\cdots +n^9}{n^{10}}\right)=\underset{n\to \infty }{\lim }\left[\sum _{i=1}^n\right(\frac{1}{n}\left)\right(\frac{i}{n}{)}^9]={\int }_0^1{x}^{9}dx$

İşte bu şekilde! İlk başta bu yöntem size dezavantajlı gelebilir. Ama aslında avantajlı olduğu kısımlar vardır. Mesela Riemann integrali kullanarak neredeyse her fonksiyonu toplama çevirip alan bulabilirsiniz.

Buna karşın klasik integral metotları için birçok farklı kural öğrenilmesi gerekir. Riemann integrali ise bunu basit kurallar ve daha çeşitli fonksiyonlar ile yapar, diğer yandan integrali olmayan veya olsa bile hesaplaması çok zor olan fonksiyonların hesaplanması için de bir alternatiftir.