Zipf Yasası: Şehir Büyüklüğü ve Kelime Kullanım Sıklığını Öngören Gizemli Yasa!
/old/content_media/65bc00b341eac2082a701786ed384e57.jpg)
- Çeviri
- Nüfus İstatistikleri
Bu Makalede Neler Öğreneceksiniz?
- Zipf Yasası, dildeki sözcüklerin kullanım sıklığı, gelir dağılımı ve şehir nüfusları gibi farklı sistemlerde, en büyük öğenin ikinci en büyüğün iki katı kadar olmasıyla kendini gösteren sıra-sıklık kuralıdır.
- Xavier Gabaix tarafından tanımlanan Zipf Yasası, büyük şehirlerin nüfus dağılımında kuvvet yasası olarak geçerlidir ancak küçük şehirlerde farklı dağılımlar gözlemlenir ve doğal şehir tanımıyla da uyumludur.
- Şehirlerin büyüme ve kaynak kullanımı ¾ kuvvet yasasına uyar; bu yasa, memelilerin metabolizma yasasıyla benzerlik gösterir ve şehirlerin doğal ekosistem benzeri enerji dağıtım sistemlerine sahip olduğunu düşündürür.
1949 yılında, dilbilimci George Zipf, belli bir dildeki sözcüklerin kullanım sıklığıyla ilgili tuhaf bir şeyin farkına vardı. Zipf’in bulgularına göre sözcüklerin büyük çoğunluğu çok nadiren kullanılırken, az sayıda birtakım sözcük çok sık kullanılıyordu. Sözcükleri kullanım sıklığına göre sıraladığında çarpıcı bir örüntü ortaya çıktı. Birinci sıradaki sözcük, ikinci sıradaki sözcüğün hep iki katı kadar sıklıkta, üçüncü sıradaki sözcüğün de hep üç katı kadar sıklıkta kullanılıyordu.
Sıra-Sıklık Kuralı adını verdiği bu kuralın herhangi bir ülkedeki gelir dağılımlarını ifade etmekte de kullanılabileceğini buldu, buna göre en zengin kişinin parası bir sonraki zengininkinin iki katı kadardı ve sıralama böyle devam ediyordu.
Daha sonra Zipf Yasası olarak adlandırılan sıra-sıklık kuralı, şehir büyüklüklerine de uygulanabilir. Bir ülkedeki en çok nüfusa sahip şehir genellikle bir sonrakinin iki katı kadardır. İnanılmaz bir şekilde, Zipf Yasası’nın şehirler uygulaması, geçen yüzyıldaki hemen her ülke için doğru çıktı.
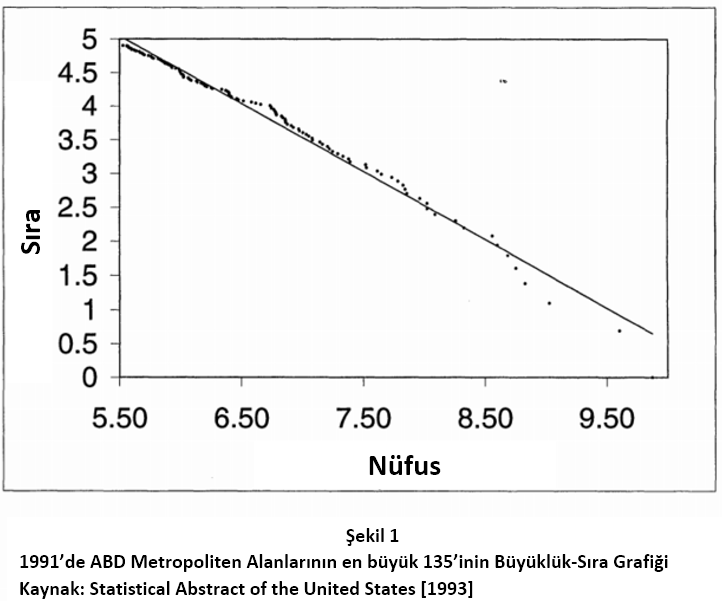
Birleşik Devletler’deki nüfusa göre en üst sıralarda yer alan şehirlere şöyle bir bakın. 2010 nüfus sayımında ABD’deki en büyük şehir olan New York’un nüfusu 8.175.133’tü. İkinci sıradaki Los Angeles’ın nüfusu 3.792.621’di. Sonraki üç sırada Chicago, Houston ve Philadelphia yer alıyordu; nüfusları sırasıyla 2.695.598, 2.100.263 ve 1.526.006’ydı. Sayıların tam olmadığını açıkça görebilirsiniz fakat istatistiksel olarak bakıldığında Zipf’in öngörülerini kayda değer biçimde tutuyorlar. [E.N.: Türkiye'deki en büyük şehirlere bakacak olursak: İstanbul 15 milyon, Ankara 5.5 milyon, İzmir 4.2 milyon, Bursa 1.8 milyon, Adana 1.7 milyon]
Zipf Yasası’nı şehirlere uygulama hakkında 2006 yılında yazan Paul Krugman herkesçe çok iyi bilinen şu ifadeleri kullanıyor:
Ekonomi kuramıyla ilgili genel şikâyet, modellerimizin çok basitleştirilmiş olduğu yönündedir; yani modellerimizin karmaşık ve dağınık gerçeği fazlasıyla düzenli bakış açılarıyla sunduğundan yakınılır. [Zipf Yasası’nda ise] tersi doğrudur: Karmaşık ve dağınık modellerimiz var, buna karşılık gerçek şaşırtıcı şekilde düzenli ve basittir.
Kuvvet Yasası
1999’da ekonomist Xavier Gabaix çok atıf alan bir makale yazdı. Bu makalede, Zipf Yasası’nın şehirler uygulamasını bir kuvvet yasası olarak tanımladı ve ABD şehirlerinin büyüklüğünü yukarıdaki ana görseldeki grafik ile gösterdi.
Gabaix, şehirler kaotik şekilde büyüse de bu kuralın hâlâ geçerli olduğunu belirtti. Ancak hem o hem de diğer ekonomistler, en üstteki mega-şehirlerden çok aşağılara indiğinizde, bu kuvvet yasasının düzgün yapısının çökme eğilimi gösterdiğine de dikkat çektiler. 100 bin kişilik nüfusun altındaki daha küçük şehirler, daha farklı bir yasaya uyuyor gibi görünmekte ve büyüklükleri daha normal bir dağılım göstermektedir.
Bu noktada, şu soruyu sorabilirsiniz: Peki, siz “şehir” dediğimiz şeyi tam olarak nasıl tanımlıyorsunuz o zaman? Bu tür hesaplamalar yaparken Boston ve Cambridge’i iki şehir veya sırf birbirlerinden su kütlesiyle ayrıldıkları için San Francisco ve Oakland’ı farklı oluşumlar olarak saymak, isteğe bağlı bir şey gibi görünüyor. İki İsveçli coğrafyacı da tamamen aynı sorunun cevabını aradılar ve siyasi sınırları uymasa da yol ve nüfus bağlantılarını temel alarak bazı bölgeleri “doğal şehirler” olarak yeniden tanımladılar. Ve bu “doğal şehirler”in bile Zipf Yasası’na uyduğunu gördüler.
/old/content_media/5636eb47e0bdd60bd8fc2d31a5bb4def.jpg) Arxiv
ArxivZipf Yasası Şehirleri Neden Etkiler?
Peki, nasıl oluyor da büyük şehirler böyle öngörülebilen bir nüfus dağılımı gösterebiliyor? Daha önce söylediğimiz gibi, hiç kimse cevabı tam olarak bilmiyor. Şehir büyüklüğünün göçle arttığını ve daha çok imkân sundukları için göçmenlerin büyük şehirlere doluşma eğiliminde olduklarını biliyoruz. Fakat göç, Gabaix’nin yukarıdaki grafiğinde gördüğümüz o mükemmel eğimi üreten kuvvet yasasını açıklamaya yeterli değildir.
Büyük şehirler daha çok zenginlik sağlama eğilimi gösterdiklerinden ekonomik nedenler şüphesiz göz önünde bulundurulmalıdır. Zipf Yasası, gelir dağılımına da uygulanabilmektedir. Fakat yine de bu kuvvet yasasının neden üst sıralardaki şehirlerde bu kadar bariz bir şekilde görüldüğünü hâlâ merak ediyoruz.
İstisnalar Var!
Geçen yıl bir grup araştırmacının Nature’da yazdığına göre Zipf Yasası’nın istisnaları da vardır. Şehirler kümesi ekonomik olarak bir bütün oluşturuyorsa ancak o zaman kuvvet yasası uygulanabiliyordu, bu da Zipf Yasası’nın neden AB’nin bütünü için değil de belli bir Avrupa ülkesinin şehirleri için geçerli olduğunu açıklamaktadır. Araştırmacıların ifadeleri şöyle:
Aslında maddi destek istememizin nedeni çok basit: Çünkü Evrim Ağacı, bizim tek mesleğimiz, tek gelir kaynağımız. Birçoklarının aksine bizler, sosyal medyada gördüğünüz makale ve videolarımızı hobi olarak, mesleğimizden arta kalan zamanlarda yapmıyoruz. Dolayısıyla bu işi sürdürebilmek için gelir elde etmemiz gerekiyor.
Bunda elbette ki hiçbir sakınca yok; kimin, ne şartlar altında yayın yapmayı seçtiği büyük oranda bir tercih meselesi. Ne var ki biz, eğer ana mesleklerimizi icra edecek olursak (yani kendi mesleğimiz doğrultusunda bir iş sahibi olursak) Evrim Ağacı'na zaman ayıramayacağımızı, ayakta tutamayacağımızı biliyoruz. Çünkü az sonra detaylarını vereceğimiz üzere, Evrim Ağacı sosyal medyada denk geldiğiniz makale ve videolardan çok daha büyük, kapsamlı ve aşırı zaman alan bir bilim platformu projesi. Bu nedenle bizler, meslek olarak Evrim Ağacı'nı seçtik.
Eğer hem Evrim Ağacı'ndan hayatımızı idame ettirecek, mesleklerimizi bırakmayı en azından kısmen meşrulaştıracak ve mantıklı kılacak kadar bir gelir kaynağı elde edemezsek, mecburen Evrim Ağacı'nı bırakıp, kendi mesleklerimize döneceğiz. Ama bunu istemiyoruz ve bu nedenle didiniyoruz.
Aslında, tarihsel olarak, bütünleştirici evrimleşmenin gözlemlendiği Avrupa’nın coğrafi düzeyi, ulusal devlettir; ABD’de ise bağımsız eyaletlerin her biri değil de tüm konfederasyon, Zipf Yasası’na uyan şehirler dağılımı yönünde, toplu bir şekilde ve birbirine bağlı olarak bir evrimleşme geçirmiştir. Bu açıdan bakıldığında ABD birbirine bağlı ve bütünleştirici bir ekonomik federasyonken AB henüz bu seviyeye gelmemiştir ve böyle bir ekonomik birim olmaya da yakın görünmemektedir. Bu da, söz konusu yasaya uyan her sistemin kendi içinde büyüklük dağılımında veya örneklerinde tutarlılığa sahip olması gerektiği anlamına gelmektedir.
Yukarıdaki ifade, Zipf Yasası’nın ekonomik duruma bir tepki olduğu fikrini destekliyor gibi görünmektedir, çünkü bu yasa, bir ülkenin şehirleri gibi birbirine ekonomik olarak bağlı olan şehirleri karşılaştırdığınızda geçerli bir yasadır.
Şehirlerin Büyüme Şekli
Şehirlere uygulanacak tuhaf bir başka kural daha vardır. ¾ kuvvet yasası diyebileceğiniz bu yasa, gelişen şehirlerin kaynak kullanımı yöntemiyle ilgilidir. Şehirler geliştikçe artan nüfusu daha fazla kaldırabilme yöntemine işaret eder. Örneğin bir şehir, büyüklüğünün iki katına çıkarsa ihtiyaç duyacağı benzin istasyonlarının sayısı iki katına çıkmaz. Onun yerine şehir sadece yaklaşık %77 daha fazla benzin istasyonuyla gayet iyi bir şekilde idare eder.
Zipf Yasası diğer sosyal yasalarla aynı yolları izler görünürken ¾ kuvvet yasası doğal bir yasaya benzer, büyümekte olan hayvanların enerjilerini nasıl kullandıklarını belirleyen yasaya. Matematikçi Steven Strogartz bunu şöyle ifade ediyor:
Örneğin farenin file göre bir günde yaktığı kalori miktarını ölçtüğünüzü varsayın. İkisi de memelidir, dolayısıyla hücresel seviyede çok farklı olmamaları gerektiğini düşünürsünüz. Gerçekte de 10 farklı memeli türünün hücreleri, konakçı organizmaları dışında ve laboratuvar doku kültüründe büyütüldüğü zaman hepsi de aynı metabolik hızı gösterdi. Sanki nereden geldiklerini bilmiyor gibiydiler, vericilerinin ne kadar büyük olduğuna dair genetik bir hafızaları yoktu.
Şimdi de fil veya fareyi bir bütün hayvan olarak düşünün, yani işlevi olan ve milyarlarca hücreden oluşan bir küme olarak. Bu durumda, ikisinin de ağırlıkları düşünüldüğünde, fil hücreleri fareninkilerden çok daha az enerji tüketir. Kleiber Yasası olarak bilinen ilgili metabolizma yasası der ki: Bir memelinin metabolik ihtiyacı, o memelinin vücut ağırlığının 0.74 çarpanı oranında artar.
Bu 0.74 çarpanı, şehirlerdeki benzin istasyonları için geçerli olan yasada gözlemlediğimiz 0.77’ye esrarengiz bir şekilde yakındır. Tesadüf mü? Belki, ama büyük olasılıkla değil. 3/4 ‘e yakın bir çarpan bulmamız için teorik sebepler vardır. Eğer kollara ayrılan bir dizi tüplerden oluşmuş daha küçük ölçekli bir şebeke kullanarak üç boyutlu bir yapının her noktasına mümkün olduğunca çabuk ve verimli bir şekilde enerji ve besin iletmek için doğal seçilim yoluyla bir taşınım dizgesi evrimleşiyor olsaydı, Santa Fe Enstitüsü’nden Geoffrey West ve meslektaşları Jim Brown ve Brian Enquist’ın iddialarına göre, bu taşınım dizgesi tam da o ¾ yasasına uyardı. Bu yapı dolaşım sistemindeki mimari yapıyla ve akciğerlerin solunum yollarıyla tam olarak örtüşürdü ve bir şehri hayatta tutmak için gereken yollar, kablolar ve borulardan da çok farklı olmazdı.
Tüm Reklamları Kapat
Bu, muhteşem büyüleyici bir şey fakat sonuçta Zipf Yasası’ndan daha az gizemli. İnsanlar tarafından inşa edilmiş olsa da özünde bir ekosistem olan şehrin doğal yasalara neden uyması gerektiğini anlamak zor olmasa gerek. Fakat Zipf Yasası’nın doğal bir benzeri yok gibi görünüyor. Bu yasa toplumsal bir yasadır ve daha önce bahsettiğim gibi sadece geçmiş 100 yıldaki şehirler için geçerlidir.
Bütün bildiğimiz Zipf Yasası’nın ekonomik ve dilbilimsel olanları da dahil olmak üzere diğer birçok toplumsal sisteme uygulanabildiğidir. Dolayısıyla, belki bir gün anlayabileceğimiz bu tuhaf sıra-büyüklük kuralını işleten genel toplumsal kuralların olması mümkündür. Kim bu kuralı çözerse kentsel büyümeden daha fazla şeyleri öngörme anahtarına sahip demektir. Zipf Yasası birbirimizle iletişim kurma, ticaret yapma ve topluluk oluşturma yöntemlerimizi sağlama bağlayan temel bir toplumsal dinamik kuralın belki de sadece bir yönüdür.
Evrim Ağacı'nda tek bir hedefimiz var: Bilimsel gerçekleri en doğru, tarafsız ve kolay anlaşılır şekilde Türkiye'ye ulaştırmak. Ancak tahmin edebileceğiniz gibi Türkiye'de bilim anlatmak hiç kolay bir iş değil; hele ki bir yandan ekonomik bir hayatta kalma mücadelesi verirken...
O nedenle sizin desteklerinize ihtiyacımız var. Eğer yazılarımızı okuyanların %1'i bize bütçesinin elverdiği kadar destek olmayı seçseydi, bir daha tek bir reklam göstermeden Evrim Ağacı'nın bütün bilim iletişimi faaliyetlerini sürdürebilirdik. Bir düşünün: sadece %1'i...
O %1'i inşa etmemize yardım eder misiniz? Evrim Ağacı Premium üyesi olarak, ekibimizin size ve Türkiye'ye bilimi daha etkili ve profesyonel bir şekilde ulaştırmamızı mümkün kılmış olacaksınız. Ayrıca size olan minnetimizin bir ifadesi olarak, çok sayıda ayrıcalığa erişim sağlayacaksınız.
Makalelerimizin bilimsel gerçekleri doğru bir şekilde yansıtması için en üst düzey çabayı gösteriyoruz. Gözünüze doğru gelmeyen bir şey varsa, mümkünse güvenilir kaynaklarınızla birlikte bize ulaşın!
Bu makalemizle ilgili merak ettiğin bir şey mi var? Buraya tıklayarak sorabilirsin.
Soru & Cevap Platformuna Git- 10
- 5
- 4
- 2
- 2
- 2
- 2
- 1
- 0
- 0
- 0
- 0
- Çeviri Kaynağı: io9 | Arşiv Bağlantısı
Evrim Ağacı'na her ay sadece 1 kahve ısmarlayarak destek olmak ister misiniz?
Şu iki siteden birini kullanarak şimdi destek olabilirsiniz:
kreosus.com/evrimagaci | patreon.com/evrimagaci
Çıktı Bilgisi: Bu sayfa, Evrim Ağacı yazdırma aracı kullanılarak 01/03/2026 04:35:09 tarihinde oluşturulmuştur. Evrim Ağacı'ndaki içeriklerin tamamı, birden fazla editör tarafından, durmaksızın elden geçirilmekte, güncellenmekte ve geliştirilmektedir. Dolayısıyla bu çıktının alındığı tarihten sonra yapılan güncellemeleri görmek ve bu içeriğin en güncel halini okumak için lütfen şu adrese gidiniz: https://evrimagaci.org/s/1814
İçerik Kullanım İzinleri: Evrim Ağacı'ndaki yazılı içerikler orijinallerine hiçbir şekilde dokunulmadığı müddetçe izin alınmaksızın paylaşılabilir, kopyalanabilir, yapıştırılabilir, çoğaltılabilir, basılabilir, dağıtılabilir, yayılabilir, alıntılanabilir. Ancak bu içeriklerin hiçbiri izin alınmaksızın değiştirilemez ve değiştirilmiş halleri Evrim Ağacı'na aitmiş gibi sunulamaz. Benzer şekilde, içeriklerin hiçbiri, söz konusu içeriğin açıkça belirtilmiş yazarlarından ve Evrim Ağacı'ndan başkasına aitmiş gibi sunulamaz. Bu sayfa izin alınmaksızın düzenlenemez, Evrim Ağacı logosu, yazar/editör bilgileri ve içeriğin diğer kısımları izin alınmaksızın değiştirilemez veya kaldırılamaz.
This work is an exact translation of the article originally published in io9. Evrim Ağacı is a popular science organization which seeks to increase scientific awareness and knowledge in Turkey, and this translation is a part of those efforts. If you are the author/owner of this article and if you choose it to be taken down, please contact us and we will immediately remove your content. Thank you for your cooperation and understanding.
/profile/7c96ff4ed6bd1f43fcd3626ac02575b0.jpeg)
/profile/2aacbbe4-281f-4f73-9317-6cfea6fc8bc0.jpeg)
/evrimagaci.org/public/images/misc/feed-support-3.png)

/evrimagaci.org/public/images/logo-50.png)