Standart Model ve Lagrange Matematiği: Evren'in Neredeyse Tamamını İzah Eden Formül Neler Anlatıyor?
:sharpen(0.5,0.5,true)/old%2Fcontent_media%2F40d6d09e4f2463a7edd00faa2dcb1ef7.jpg) Business Recorder
Business Recorder
Bu Makalede Neler Öğreneceksiniz?
- Standart Model, elektromanyetizma, zayıf ve güçlü çekirdek kuvvetlerini açıklayan, Higgs Bozonu keşfiyle desteklenen ancak kütleçekimini içermediği için eksik kalan temel parçacık fiziği modelidir.
- Modelin Lagrange denklemi beş ana kısımdan oluşur ve bu kısımlar güçlü nükleer kuvveti, bozonlar arası etkileşimleri, zayıf nükleer kuvveti, parçacıkların Higgs Alanı ile etkileşimini ve Faddeev-Popov hayaletlerini tanımlar.
- Zayıf kuvvet bölümünde nötrinoların kütlelerinin varlığı keşfedilerek modelin bazı varsayımları sorgulanmış ve parçacık fiziğinde önemli bir bilimsel gelişme sağlanmıştır.
Standart Model, fizikçilerin Evren'i açıklamak için kullandıkları atom altı parçacıkları ve bunların birbiriyle ilişkilerini izah eden modeldir. Bu model, elektromanyetizma, zayıf çekirdek kuvveti ve güçlü çekirdek kuvvetini içerir. Özellikle kuarkların keşfiyle birlikte güç kazanmış ve doğrulanmıştır. Ne yazık ki, şu anda kütleçekimini içermediği için tüm temel kuvvetleri bir arada izah edebilen bir model değildir. Bu model, teorik olarak sağlam olsa da, pratikteki uygulamalarında bazı açıklanamayan olgularla karşılaşılmıştır. Higgs Bozonu'nun keşfi, bu modeli tamamlayıcı ve bütünleştirici nitelikte olmuştur. Ancak halen modelin geliştirilmeye ihtiyacı bulunmaktadır.
Standart Model'i normalde parçacıkları ve özelliklerini gösteren tablolar ile görmeye alışık olsak da, Lagrange Matematiği kullanılarak, görseldeki gibi ifade etmek de mümkündür. Lagrange Matematiği'nin güzel tarafı, durmaksızın değişen bir sistemin her bir durumunu ve sistemin barındırabileceği maksimum enerji miktarını ifade etmekte kullanılabilecek olmasıdır. Elbette, bu matematiği kullanmak şart değildir ve Standart Model'i başka şekillerde formülize etmek de mümkündür; ancak görseldeki versiyon, en meşhur ve parçaların bir bütün olarak görülebildiği gösterimlerinden birisidir. Denklem, şöyledir:
:sharpen(0.5,0.5,true)/old%2Fcontent_media%2F1a3d1f5be99314c16f5a882e66ba07e5.png)
Denklemi Parçalara Bölmek
Bu akıl almaz uzunluktaki denklem, 5 alt kısımdan oluşur:
:sharpen(0.5,0.5,true)/old%2Fcontent_media%2Fc0e17916447cde4c0e5680fbfaae6356.png)
Kısım kısım inceleyecek olursak:
1. Kısım: Güçlü Nükleer Kuvvet ve Gluonlar
:sharpen(0.5,0.5,true)/old%2Fcontent_media%2F606a3afe6c4d283e4433eca4d3379533.png)
Bu kısım, Güçlü Nükleer Kuvvet'i taşıyan gluonları tanımlayan kısımdır. 8 çeşit gluon bulunmaktadır ve bunların her birinin birbiriyle çeşitli şekillerde etkileşimi bulunmaktadır. Gluonların renk yükü vardır. "Renk yükü" kavramının, bildiğimiz "renk" kavramı ile hiçbir alakası yoktur. Fizikçiler tarafından, renk yüklerinin alışageldiğimiz kırmızı, yeşil, mavi gibi renklerle aşırı yüzeysel bir benzerliği bulunduğu için bu isim seçilmiştir. Ama benzerlik öylesine yüzeyseldir ki, Richard Feynman bu kafa karıştırıcı ismi seçen fizikçileri "aptallar" olarak tanımlamıştır.
2. Kısım: Bozonlar Arası Etkileşim
:sharpen(0.5,0.5,true)/old%2Fcontent_media%2F3d1e6ed8b248f79b6558e68336fbdac9.png)
Denklemin neredeyse yarısını oluşturan bu kısım, bozonlar arası etkileşimi izah etmektedir. Özellikle de W ve Z bozonlarına odaklanır. Bozonlar, kuvvet taşıyan parçacıklardır ve 4 çeşit bozon birbiriyle etkileşerek 3 temel kuvveti oluştururlar: Işığın yapısından tanıdığımız ve bir bozon olan fotonlar Elektromanyetik Kuvvet'i taşır, gluonlar az önce sözünü ettiğimiz gibi Güçlü Nükleer Kuvvet'i taşır; W ve Z bozonları ise Zayıf Nükleer Kuvvet'i taşır. Yakınlarda keşfedilen Higgs Bozonu ise birazcık daha farklıdır. Bu nedenle bu bozonun, denklemde kendine ait bir kısmı vardır. Bu da bizi, bir sonraki kısma götürüyor.
3. Kısım: Zayıf Nükleer Kuvvet
:sharpen(0.5,0.5,true)/old%2Fcontent_media%2F1552eb6ab13a5c2277809c271567e91a.png)
Denklemin bu kısmı, temel madde parçacıklarının Zayıf (Nükleer) Kuvvet ile nasıl etkileştiğini açıklamaktadır. Bu formülasyona göre madde parçacıkları 3 nesle ayrılır ve her birinin ayrı kütlesi bulunur. Zayıf Kuvvet, daha yüksek kütleli madde parçacıklarının daha düşük kütlelilere bozunmasına yardımcı olur. Bu kısımda aynı zamanda Higgs Alanı da tanımlanmaktadır. Bu alan, bazı temel parçacıklara kütlesini kazandırmaktadır. İlginç bir şekilde, denklemin bu kısmı fizikçilerin yakın geçmişteki bazı keşiflerine ters düşen varsayımları içermektedir. Hatalı bir şekilde, nötrinoların kütlesi olduğu varsayılmıştır; ancak 1998 yılında fizikçiler nötrinoların da aşırı küçük ama sıfırdan büyük kütleli olduğunu ortaya koymuşlardır. Bu, on yıllardır parçacık fiziğinin temel varsayımlarından birini alt üst etmiştir.
4. Kısım: Parçacıklar ve Higgs Alanı
:sharpen(0.5,0.5,true)/old%2Fcontent_media%2F16e9644306698996400fcf35fb199963.png)
Kuantum mekaniğinde bir parçacığın gidebileceği tek bir yol veya yörünge bulunmamaktadır. Dolayısıyla bu parçacıkların hareketlerini tanımlayan matematiksel formüllerde kimi zaman fazladan terimler bulunur. Teorik fizikçiler, bu fazladan terimleri temizlemek için "sanal parçacık" denen bir olguya başvururlar. Bunlar, gerçekte parçacık değillerdir. Sadece, parçacıkların fiziksel "alanlar" ile etkileşiminin ürünü olan bozulmalardır (İng: "disturbance"). Kimi zaman bunları "hayaletler" olarak tanımlamak da mümkündür. Ancak Feynman'dan azar yememek için, bunların "paranormal" bir olgu olduğu iddia edilen ve gerçekte bulunmayan "hayaletler" ile hiçbir ilgisi olmadığının altını çizmek gerekiyor. Nasıl ki bu tip klişe filmlerde, hayaletlerin gerçek dünyaya etkisi bu dünyada bir çeşit "bozulmaya" neden oluyorsa, fiziksel parçacıkların çeşitli fiziksel alanlar üzerindeki etkileri de bu şekilde "bozulmalara" neden olmaktadır.
İşte denklemin bu kısmı, parçacıkların Higgs Alanı ile etkileşmesi sonucu bu alandaki bozulmaları tanımlamaktadır.
5. Kısım: Faddeev-Popov Hayaletleri
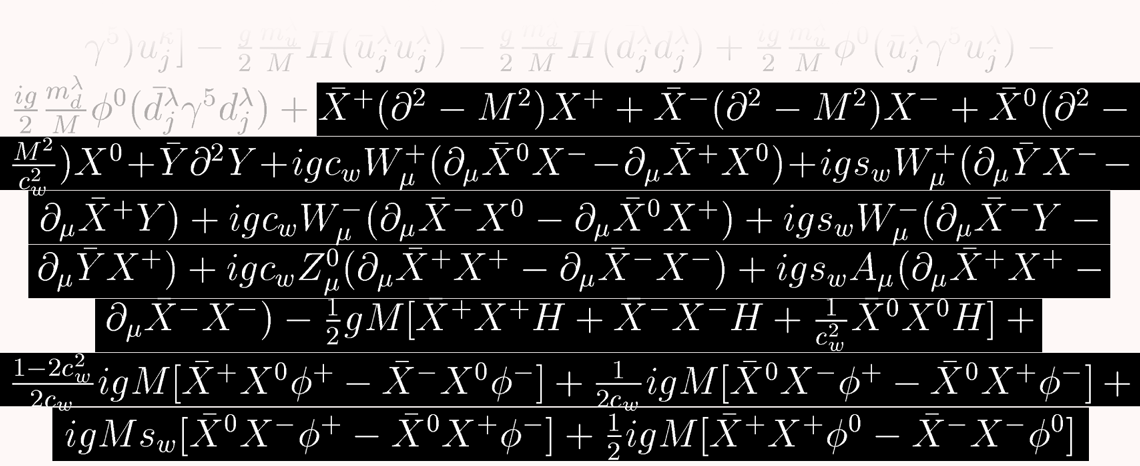
Denklemin son kısmında ise daha da fazla "hayalet" kullanılmaktadır. Burada gösterilen terimler, Faddeev-Popov Hayaletleri'dirler. Bu terimlerin amacı, Zayıf Kuvvet ile etkileşimi tanımlarken doğan bazı diğer fazladan terimleri denkleştirmektir.
Aslında maddi destek istememizin nedeni çok basit: Çünkü Evrim Ağacı, bizim tek mesleğimiz, tek gelir kaynağımız. Birçoklarının aksine bizler, sosyal medyada gördüğünüz makale ve videolarımızı hobi olarak, mesleğimizden arta kalan zamanlarda yapmıyoruz. Dolayısıyla bu işi sürdürebilmek için gelir elde etmemiz gerekiyor.
Bunda elbette ki hiçbir sakınca yok; kimin, ne şartlar altında yayın yapmayı seçtiği büyük oranda bir tercih meselesi. Ne var ki biz, eğer ana mesleklerimizi icra edecek olursak (yani kendi mesleğimiz doğrultusunda bir iş sahibi olursak) Evrim Ağacı'na zaman ayıramayacağımızı, ayakta tutamayacağımızı biliyoruz. Çünkü az sonra detaylarını vereceğimiz üzere, Evrim Ağacı sosyal medyada denk geldiğiniz makale ve videolardan çok daha büyük, kapsamlı ve aşırı zaman alan bir bilim platformu projesi. Bu nedenle bizler, meslek olarak Evrim Ağacı'nı seçtik.
Eğer hem Evrim Ağacı'ndan hayatımızı idame ettirecek, mesleklerimizi bırakmayı en azından kısmen meşrulaştıracak ve mantıklı kılacak kadar bir gelir kaynağı elde edemezsek, mecburen Evrim Ağacı'nı bırakıp, kendi mesleklerimize döneceğiz. Ama bunu istemiyoruz ve bu nedenle didiniyoruz.
Denklemde İşaret Hatası!
İlginç bir şekilde, bu denklemi derli toplu bir araya getirip internete yükleyen, California Politeknik Eyalet Üniversitesi profesörlerinden Dr. Thomas Gutierrez, ana görseldeki denklemi incelerken bir işaret hatası olduğunu ama bunu bulacak enerjisi olmadığını belirtmiştir. Bu hatayı bulabilecek misiniz?
Evrim Ağacı'nda tek bir hedefimiz var: Bilimsel gerçekleri en doğru, tarafsız ve kolay anlaşılır şekilde Türkiye'ye ulaştırmak. Ancak tahmin edebileceğiniz gibi Türkiye'de bilim anlatmak hiç kolay bir iş değil; hele ki bir yandan ekonomik bir hayatta kalma mücadelesi verirken...
O nedenle sizin desteklerinize ihtiyacımız var. Eğer yazılarımızı okuyanların %1'i bize bütçesinin elverdiği kadar destek olmayı seçseydi, bir daha tek bir reklam göstermeden Evrim Ağacı'nın bütün bilim iletişimi faaliyetlerini sürdürebilirdik. Bir düşünün: sadece %1'i...
O %1'i inşa etmemize yardım eder misiniz? Evrim Ağacı Premium üyesi olarak, ekibimizin size ve Türkiye'ye bilimi daha etkili ve profesyonel bir şekilde ulaştırmamızı mümkün kılmış olacaksınız. Ayrıca size olan minnetimizin bir ifadesi olarak, çok sayıda ayrıcalığa erişim sağlayacaksınız.
Makalelerimizin bilimsel gerçekleri doğru bir şekilde yansıtması için en üst düzey çabayı gösteriyoruz. Gözünüze doğru gelmeyen bir şey varsa, mümkünse güvenilir kaynaklarınızla birlikte bize ulaşın!
Bu makalemizle ilgili merak ettiğin bir şey mi var? Buraya tıklayarak sorabilirsin.
Soru & Cevap Platformuna Git- 97
- 48
- 47
- 30
- 25
- 23
- 12
- 10
- 6
- 2
- 0
- 0
- R. Shivni. The Deconstructed Standard Model Equation. (28 Temmuz 2016). Alındığı Tarih: 4 Ocak 2019. Alındığı Yer: Symmetry Magazine | Arşiv Bağlantısı
- M. Strassler. Virtual Particles: What Are They?. (4 Ocak 2019). Alındığı Tarih: 4 Ocak 2019. Alındığı Yer: Of Particular Significance | Arşiv Bağlantısı
Evrim Ağacı'na her ay sadece 1 kahve ısmarlayarak destek olmak ister misiniz?
Şu iki siteden birini kullanarak şimdi destek olabilirsiniz:
kreosus.com/evrimagaci | patreon.com/evrimagaci
Çıktı Bilgisi: Bu sayfa, Evrim Ağacı yazdırma aracı kullanılarak 08/02/2026 09:11:43 tarihinde oluşturulmuştur. Evrim Ağacı'ndaki içeriklerin tamamı, birden fazla editör tarafından, durmaksızın elden geçirilmekte, güncellenmekte ve geliştirilmektedir. Dolayısıyla bu çıktının alındığı tarihten sonra yapılan güncellemeleri görmek ve bu içeriğin en güncel halini okumak için lütfen şu adrese gidiniz: https://evrimagaci.org/s/866
İçerik Kullanım İzinleri: Evrim Ağacı'ndaki yazılı içerikler orijinallerine hiçbir şekilde dokunulmadığı müddetçe izin alınmaksızın paylaşılabilir, kopyalanabilir, yapıştırılabilir, çoğaltılabilir, basılabilir, dağıtılabilir, yayılabilir, alıntılanabilir. Ancak bu içeriklerin hiçbiri izin alınmaksızın değiştirilemez ve değiştirilmiş halleri Evrim Ağacı'na aitmiş gibi sunulamaz. Benzer şekilde, içeriklerin hiçbiri, söz konusu içeriğin açıkça belirtilmiş yazarlarından ve Evrim Ağacı'ndan başkasına aitmiş gibi sunulamaz. Bu sayfa izin alınmaksızın düzenlenemez, Evrim Ağacı logosu, yazar/editör bilgileri ve içeriğin diğer kısımları izin alınmaksızın değiştirilemez veya kaldırılamaz.
:sharpen(0.5,0.5,true)/profile%2F2aacbbe4-281f-4f73-9317-6cfea6fc8bc0.jpeg)
:sharpen(0.5,0.5,true)/evrimagaci.org%2Fpublic%2Fimages%2Fmisc%2Ffeed-support-2.png)

:sharpen(0.5,0.5,true)/evrimagaci.org%2Fpublic%2Fimages%2Flogo-50.png)