Işık Hızı Neden "c" ile Gösterilir?

“Fizikçiye Sorun” gelen kutumuzdaki (iç karartıcı bir çoğunlukla “Fiziğe Sorun” olarak anlaşılmış), tüm sorularınızı inceliyoruz, ama özellikle ışık hızı konusu sıklıkla insanların hayal gücünün kıvılcımlarını harekete geçiriyor ve merakını tetikliyor. Bu hızı tanımlayan nedir ve bu hızın üzerine neden çıkamıyoruz? Bu hızın üzerine çıkmayı denersek ne olur? Bu sorular üzerine düşünmek ve cevaplarını bulmaya çalışmak başlı başına çekici ve eğlenceli. Ama asıl önemli olan ise, bu sorularla uğraşmak ve cevaplandırmak evrenin temelindeki kuralları kavramamızı sağlıyor. Bugün bu sorulardan birini ele alacağız ve kasti bir kelime oyunu olmaksızın bu soruyu aydınlatacağız. Işık hızı neden boşlukta 300,000,000 m/s? Neden “c”?

İki yönde de sonsuza kadar uzanan yüklü bir teliniz olduğunu hayal edin. Sonsuz olduğundan, üstündeki toplam yükten bahsetmek çok zordur; bunu yapmamız ancak teli küre gibi kapalı bir alanın içinde sınırlamakla olabilir. Buna rağmen, örneğin sınırlı uzunluktaki bir telden bahsedersek, her metresindeki yükün miktarından yani yük yoğunluğundan konuşabiliriz.

Sonsuz bir tel, uzunluğu üzerindeki her noktada aynı görünür. Bu tel üzerindeki yük sebebiyle ortaya çıkan elektriksel alanın büyüklüğünü yani yüklü parçacıkların tel üstündeki yüklerden nasıl etkilendiğini veya nasıl itildiğini düşündüğünüzde, bunun yalnızca telin yük yoğunluğuna ve etkilediği parçacığın tele olan uzaklığına bağlı olduğunu anlayacaksınız. Bu arada bizim amacımıza ulaşmak içi kullandığımız ortam olan havasız ortam, uzay boşluğu, elektriksel geçirgenlik olarak orta seviye olacak. Bahsettiğimiz tel etrafındaki elektriksel alanın büyüklüğünü gösteren formül aşağıdaki gibidir:

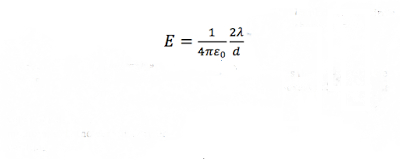
Şimdi şu sonsuz uzunluk işini bir kenara bırakalım, birinin bu teli makaraya sardığını ve sonra onu ekseni boyunca hareket ettirdiğini düşünelim. Nereden bakılırsa bakılsın, bu hareket yükün tel içinde hareketini sağlamaktan ziyade, bir akım yaratacak. (Bir uçtaki voltajı değiştirerek yapacaksınız.) Şu an telin kendisini içerdiği yükle beraber hareket ettiriyoruz. Nedenine gelince, bunu birazdan umuyoruz ki göreceksiniz.

Bildiğiniz gibi, telden geçen bir akım, telin etrafında bir çember şeklinde manyetik alan oluşturur. Bu manyetik alanın büyüklüğü, telden uzaklığınıza (d) ve tabii ki telin yük yoğunluğu ve çekilme hızına bağlı olarak oluşan akımın gücüne bağlıdır.

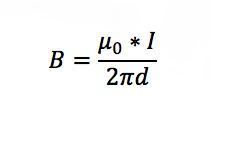
Şimdi bu telin ilkine paralel, aynı voltajda yüklü ve aynı yönde, aynı hızda çekilen bir ikincisine daha sahip olduğunuzu hayal edin. Yüklerden dolayı, iki tel birbirini elektrostatik itmelerinden dolayı birbirilerini iterler.

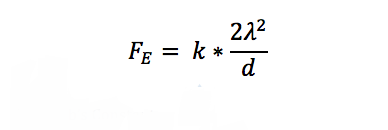
İki yüklü nesnenin arasındaki kuvveti hesaplarken, nesnelerin yükleri birlikte çarpılır, çünkü her bir kablo lambda kadar yüke sahiptir.

Tellerin üzerindeki statik elektrik yükleri, bu tellerin birbirlerini itmesini sağlar. Ancak, bu teller aynı yöne çekildiği için, iki tel birden etkili bir akıma sahip olur ve bu akımlara bir manyetik alan da eşlik eder. İki paralel tel üzerinde aynı yönde iki akım elde ettiğinizde, bu iki telin manyetik alanı teller arasında daha etkili bir kuvvet oluşmasına neden olur.

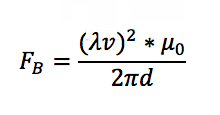
Eğer yakından takip ederseniz, bahsettiğimiz senaryoda teller arası manyetik kuvvetin, teller arasındaki itici elektriksel kuvveti etkisiz hale getirdiğini göreceksiniz. Yukarıdaki eşitlikte de gördüğünüz gibi, manyetik kuvvetin büyüklüğü, elektriksel kuvvetten –ki fizikte buna direkt elektrostatik deniyor- farklı olarak, tellerin ne kadar hızlı olduğuna bağlı. Peki, telin elektriksel itme kuvvetinin manyetik kuvvetle iptal edilebilmesi için teli ne kadar hızlı hareket ettirmelisiniz? Bu sorunun cevabını, iki denklemi aşağıdaki gibi birbirine eşitleyerek ve bu denklemden de v’yi çekerek bulabiliriz.

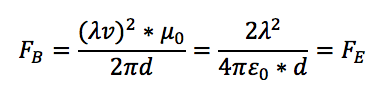
Ufak bir cebir bilgisi parantezleri yok etmemize ve eşitliğin sağ tarafındaki kesri azaltmamıza yardımcı olacak:

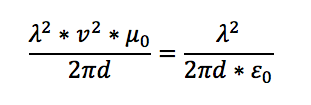
Bu adımda karşımıza şaşırtıcı bir sonuç çıkıyor: Yük yoğunluğu eşitliğin her iki tarafında da aynı güçte ve aynı yerlerde; bu demektir ki yük yoğunlukları birbirini götürecek. Yani eletriksel ve manyetik kuvvetin birbirine eşit olduğu durumda tellerin yüklerinin büyüklüğü bizi ilgilendirmiyor. 2*pi*d çarpanları da aynı sebepten ötürü birbirlerini götürecek, yani teller arasındaki uzaklığın da bu eşitlik için pek bir önemi yok. Tüm bu işe yaramaz terimleri ayırdığımızda eşitlik şuna dönüyor:

Evrim Ağacı'ndan Mesaj

Neden Desteğe İhtiyacımız Var?

Aslında maddi destek istememizin nedeni çok basit: Çünkü Evrim Ağacı, bizim tek mesleğimiz, tek gelir kaynağımız. Birçoklarının aksine bizler, sosyal medyada gördüğünüz makale ve videolarımızı hobi olarak, mesleğimizden arta kalan zamanlarda yapmıyoruz. Dolayısıyla bu işi sürdürebilmek için gelir elde etmemiz gerekiyor.

Bunda elbette ki hiçbir sakınca yok; kimin, ne şartlar altında yayın yapmayı seçtiği büyük oranda bir tercih meselesi. Ne var ki biz, eğer ana mesleklerimizi icra edecek olursak (yani kendi mesleğimiz doğrultusunda bir iş sahibi olursak) Evrim Ağacı'na zaman ayıramayacağımızı, ayakta tutamayacağımızı biliyoruz. Çünkü az sonra detaylarını vereceğimiz üzere, Evrim Ağacı sosyal medyada denk geldiğiniz makale ve videolardan çok daha büyük, kapsamlı ve aşırı zaman alan bir bilim platformu projesi. Bu nedenle bizler, meslek olarak Evrim Ağacı'nı seçtik.

Eğer hem Evrim Ağacı'ndan hayatımızı idame ettirecek, mesleklerimizi bırakmayı en azından kısmen meşrulaştıracak ve mantıklı kılacak kadar bir gelir kaynağı elde edemezsek, mecburen Evrim Ağacı'nı bırakıp, kendi mesleklerimize döneceğiz. Ama bunu istemiyoruz ve bu nedenle didiniyoruz.

Destek Ol

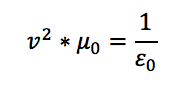
Ve son olarak v için elimizde şu eşitlik kalıyor:

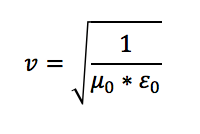
Eğer bu denkleme boşluğun dielektrik sabitinin ve elektriksel geçirgenliğinin gerçek değerlerini yazarsanız, denklem size 299,792,400 m/s gibi ışık hızına çok yakın bir değer verir.

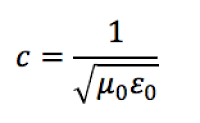
Peki, bu ne anlama gelir? İlk olarak, gerçekte bir teli asla manyetik kuvveti elektriksel kuvvetini tamamen sıfırlayacak kadar hızlı sallayamazsınız, çünkü ışık hızında hareket edebilecek kadar çok büyük bir nesne yok. Daha önemlisi, ışığın boşluktaki hızının ne olduğuna ve neden olduğu hakkında bize ipucu veriyor: Işığın boşluktaki hızı, ışığın sınırsızca hareket etmesine olanak sağlayacak, elektrik ve manyetik kuvvetlerin denge durumunda oluşturduğu sabit bir elektromanyetik dalgadır. Herhangi bir yavaşlama ve foton yok olur, teller biribirini elektriksel itme kuvvetiyle iter. Herhangi bir hızlanma ve manyetizma üstün gelir, teller birbirini çeker, sistem göçer. Lise matematiğinden fazlası olmaksızın, ışık hızının ortalama geçirgenlikteki bir ortamda, uzay boşluğunda, ortamın elektriksel geçirgenliğinin ve manyetik geçirgenliğinin bir sonucu olarak oluştuğunu kolayca gösterdik.

Biliyorum bu yazı, bir blog yazısı için son derece fazla matematik içeriyordu. Umuyorum ki bu yaptıklarımız size fiziğin heyecanlı ve bağımlılık yaratan diğer konularına göz atma isteği vermiştir. Potansiyelinizi ilerletmek ve evrensel gerçekleri keşfetmek için biraz matematik ve hayal gücünden fazlasına ihtiyacınız yok.