Nükleer Fizik: Yarı Ömür ve Bozunum Sabiti

- Özgün
Radyoaktif izotoplar, yüksek sayıda radyoaktif çekirdekten oluşurlar. Bu çekirdeklerin hepsi, aynı andabozunmazlar. Yukarıda dediğimiz gibi, süreç tamamen rasgeledir.
Verilen bir çekirdeğin ne zaman bozunacağını öngöremeyiz. Lakin, verilen bir örneğin ne kadarının verilen zaman aralığında bozunacağını hesaplayabiliriz.
Bu hesaplamayı yaparken, radyoaktif materyaldeki tüm çekirdeklerin bozunma ihtimalinin aynı olduğunu kabul ederiz.
Basitçe diyebiliriz ki bozunum miktarı, geçen zamanla doğru orantılıdır. Ayrıca, yine bozunum miktarı, elimizdeki örneğin içinde bulunan radyoaktif çekirdek sayısıyla da doğru orantılıdır. Yani:
ΔN∝ Δt
ve
ΔN ∝ N
dN∝Ndt
dN = - λN dt
4 numaralı denklem, çözümü oldukça basit olan bir diferansiyel denklemdir (ancak henüz diferansiyel denklemleri çözmeyi bilmiyorsanız da canınızı sıkmayın, denklem 5 ile 6'yı geçebilirsiniz).
Şimdi de her iki tarafın integralini alalım. Aşağıdaki integrallerin sınırları, radyoaktif çekirdek miktarı olan N'in, N_0 a düşmesini ve zaman aralığının 0'dan rasgele bir deger olan t'ye kadar çıkmasını ifade eder.
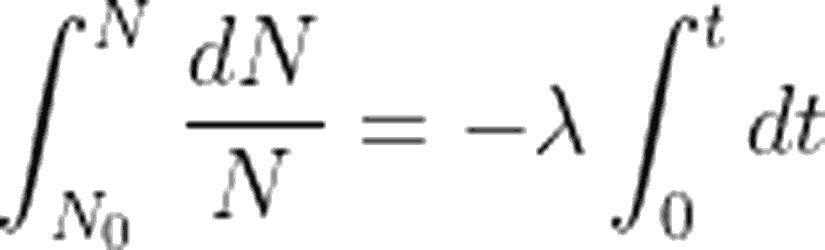
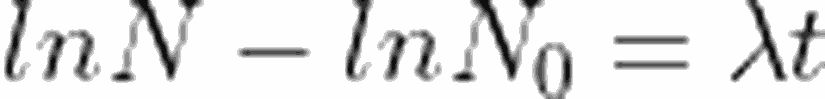
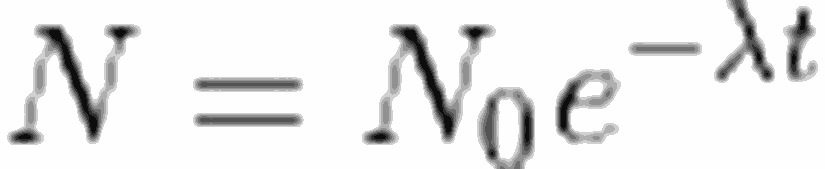
Nükleer Aktivite
Birim zamandaki bozunum miktarı nükleer aktivite olarak adlandırılır ve R ile gösterilir. Birim zamandaki bozunum miktarını, aşağıdaki gibi ifade edebiliriz.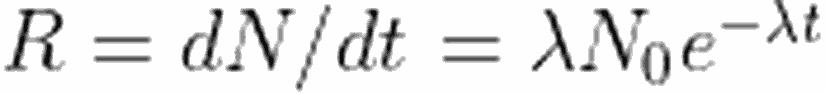
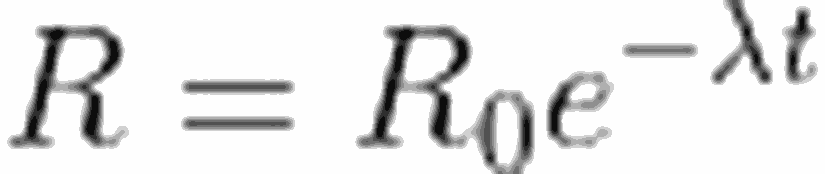
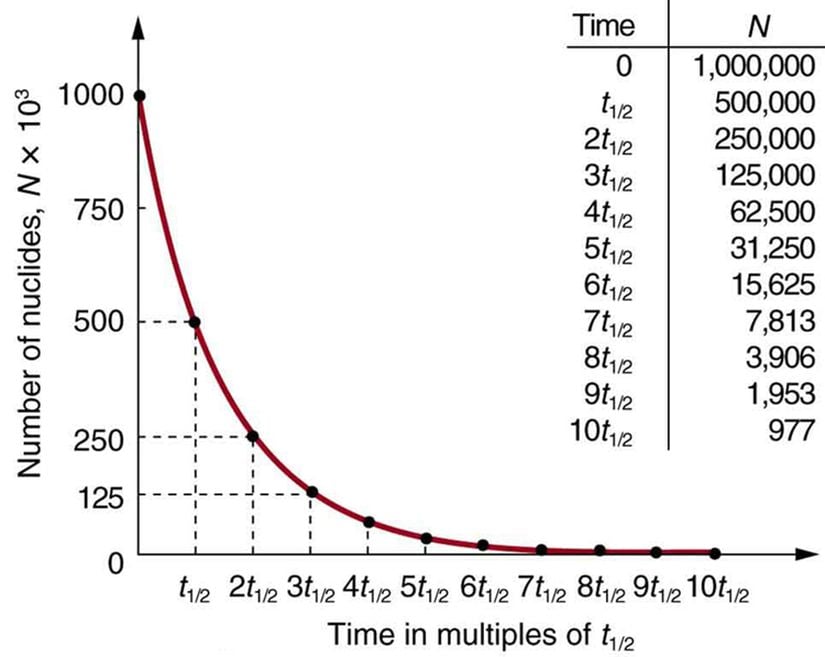
Yarı Ömür
Yarı ömür; aktiviteyi ya da radyoaktif çekirdek sayısını yarıya düşürmek için gereken zaman olarak tanımlanabilir. Radyoaktif elementler, 1 μs ile 10^9 yıl arasında değişen bir yarı ömre sahip olabilirler. Verdiğimiz tanımdan yola çıkarak, yarı ömrü şu şekilde ifade edebiliriz:Yarılanma süresi
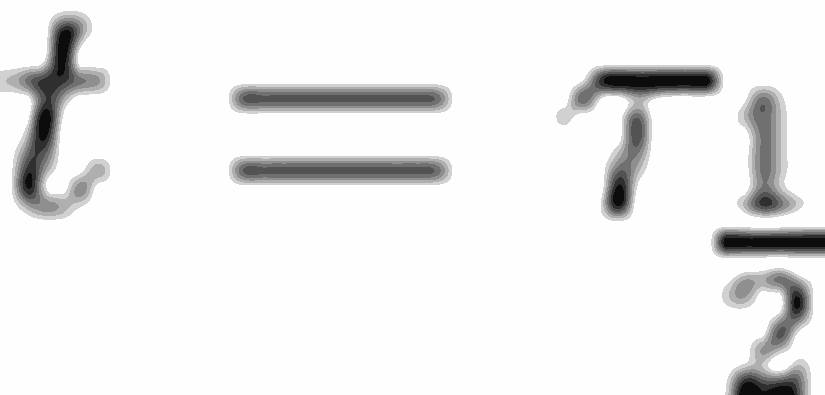
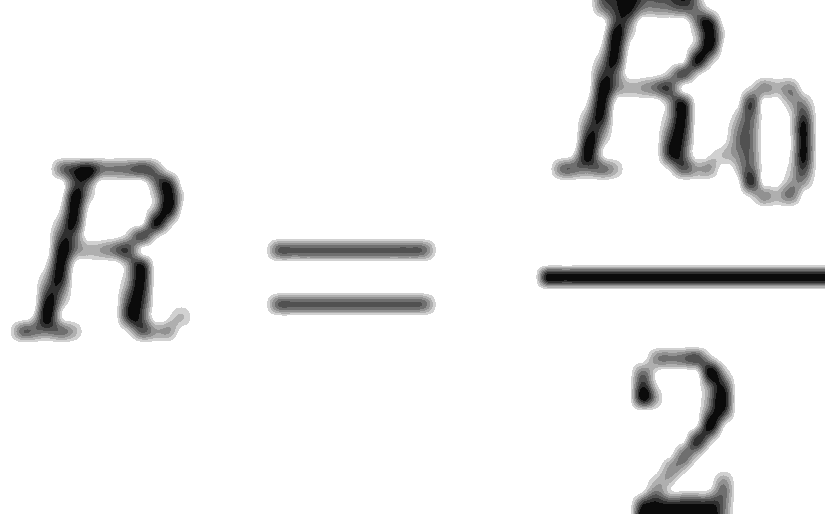
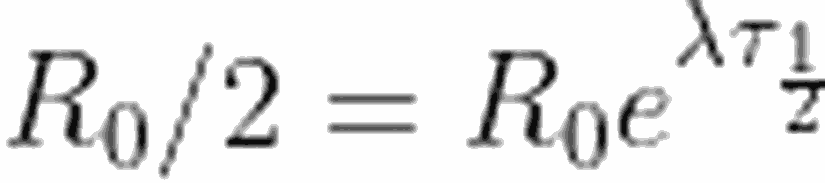
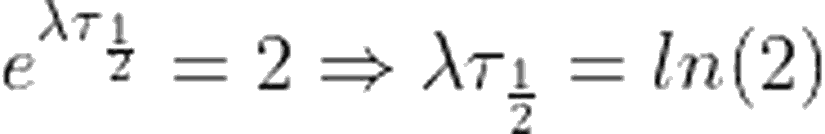
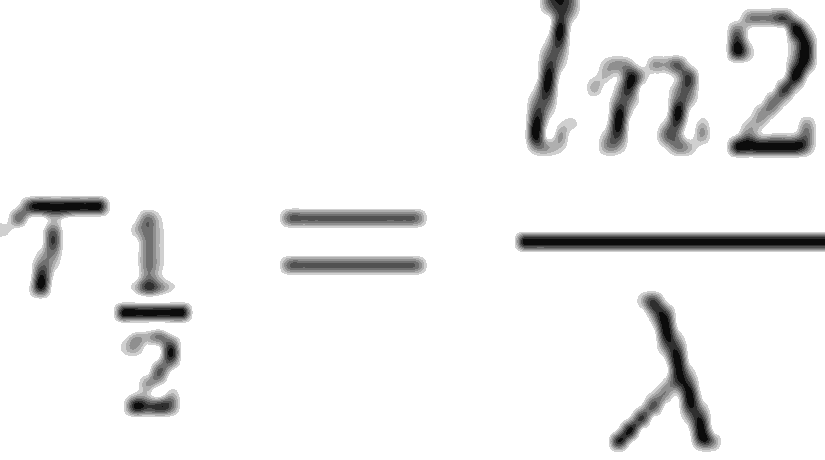
Örnek
Bir örnek, bu konsepti pekiştirmemize yardımcı olacaktır. Saniyede 3.7 x 10^4 adet α parçacığı yayan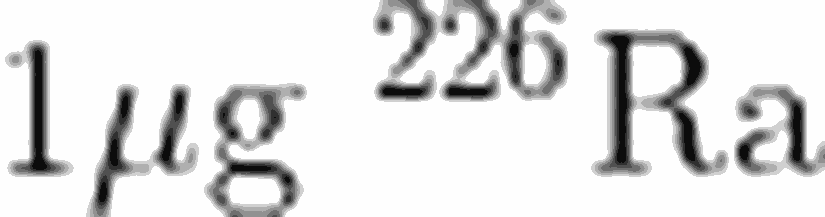
Öncelikle, 1 μg'nin kaç tane atomdan oluştuğunu bulmamız gerekir. elementin atom ağırlığı
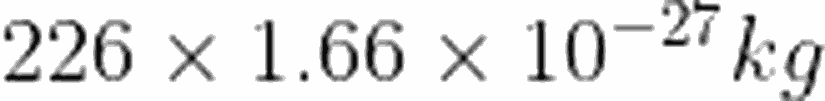

8 numaralı denklemin sağ tarafı yani
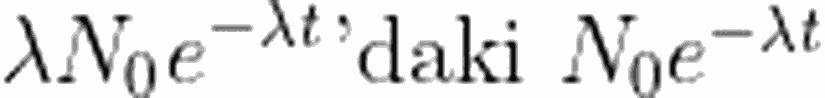
R= Nλ
Öyleyse,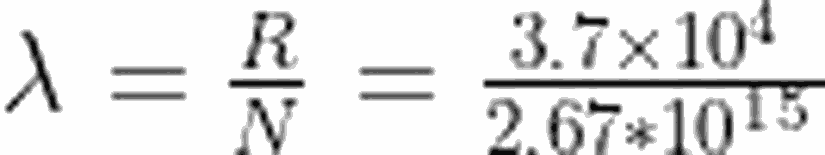
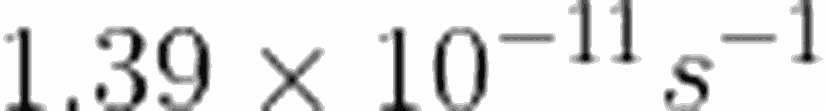
Yazımızda, Nükleer fiziğin en önemli konularından birisi olan yarı ömrünü inceledik. Bu sayede, elementin yarı ömrünün ne anlama geldiğini ve nükleer bozunumlardaki rasgeleliği daha iyi kavramış olduk.
Ege Can KARANFİL
Referanslar
- Prof. Dr. Selahattin Özdemir, Health Physics ders notları
- Lumen, "Half-Life and Activity"
<https://courses.lumenlearning.com/physics/chapter/31-5-half-life-and-activity/>
Evrim Ağacı'nda tek bir hedefimiz var: Bilimsel gerçekleri en doğru, tarafsız ve kolay anlaşılır şekilde Türkiye'ye ulaştırmak. Ancak tahmin edebileceğiniz gibi Türkiye'de bilim anlatmak hiç kolay bir iş değil; hele ki bir yandan ekonomik bir hayatta kalma mücadelesi verirken...
O nedenle sizin desteklerinize ihtiyacımız var. Eğer yazılarımızı okuyanların %1'i bize bütçesinin elverdiği kadar destek olmayı seçseydi, bir daha tek bir reklam göstermeden Evrim Ağacı'nın bütün bilim iletişimi faaliyetlerini sürdürebilirdik. Bir düşünün: sadece %1'i...
O %1'i inşa etmemize yardım eder misiniz? Evrim Ağacı Premium üyesi olarak, ekibimizin size ve Türkiye'ye bilimi daha etkili ve profesyonel bir şekilde ulaştırmamızı mümkün kılmış olacaksınız. Ayrıca size olan minnetimizin bir ifadesi olarak, çok sayıda ayrıcalığa erişim sağlayacaksınız.
Makalelerimizin bilimsel gerçekleri doğru bir şekilde yansıtması için en üst düzey çabayı gösteriyoruz. Gözünüze doğru gelmeyen bir şey varsa, mümkünse güvenilir kaynaklarınızla birlikte bize ulaşın!
Bu makalemizle ilgili merak ettiğin bir şey mi var? Buraya tıklayarak sorabilirsin.
Soru & Cevap Platformuna Git- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
Evrim Ağacı'na her ay sadece 1 kahve ısmarlayarak destek olmak ister misiniz?
Şu iki siteden birini kullanarak şimdi destek olabilirsiniz:
kreosus.com/evrimagaci | patreon.com/evrimagaci
Çıktı Bilgisi: Bu sayfa, Evrim Ağacı yazdırma aracı kullanılarak 09/05/2025 22:35:39 tarihinde oluşturulmuştur. Evrim Ağacı'ndaki içeriklerin tamamı, birden fazla editör tarafından, durmaksızın elden geçirilmekte, güncellenmekte ve geliştirilmektedir. Dolayısıyla bu çıktının alındığı tarihten sonra yapılan güncellemeleri görmek ve bu içeriğin en güncel halini okumak için lütfen şu adrese gidiniz: https://evrimagaci.org/s/12629
İçerik Kullanım İzinleri: Evrim Ağacı'ndaki yazılı içerikler orijinallerine hiçbir şekilde dokunulmadığı müddetçe izin alınmaksızın paylaşılabilir, kopyalanabilir, yapıştırılabilir, çoğaltılabilir, basılabilir, dağıtılabilir, yayılabilir, alıntılanabilir. Ancak bu içeriklerin hiçbiri izin alınmaksızın değiştirilemez ve değiştirilmiş halleri Evrim Ağacı'na aitmiş gibi sunulamaz. Benzer şekilde, içeriklerin hiçbiri, söz konusu içeriğin açıkça belirtilmiş yazarlarından ve Evrim Ağacı'ndan başkasına aitmiş gibi sunulamaz. Bu sayfa izin alınmaksızın düzenlenemez, Evrim Ağacı logosu, yazar/editör bilgileri ve içeriğin diğer kısımları izin alınmaksızın değiştirilemez veya kaldırılamaz.



