Kuantum Mekaniği: Kara Cisim Işımasının Temelleri

Cisimler, çevreleri ile her zaman termodinamik bir etkileşim içindedirler. Fiziksel bir çok yol ile enerji alışverişi gerçekleştirirler. Bu yazımızda konusu da bunlardan biri olanışıma ve klasik mekaniğin yetersiz kaldığı bu fiziksel etkileşimde süperkahraman rolü üstlenip kuantum mekaniği ile bizleri aydınlığa kavuşturan Max Planck.
Cisimler, ışıma ile enerji alabilir ya da kaybedebilir. Enerji alışverişini sağlayan bu ışıma, termodinamikte özel olarak termal (ısısal) ışıma adını alır. Cismin yaptığı ışımanın hızı, A yüzey alanıyla ve T sıcaklığıyla doğru orantılıdır. Işıma hızı şu şekilde ifade edilebilir:

Bu denklemdeki "σ" Stefan-Boltzmann sabitidir. "ε" ise yüzeyin ışıma gücünü ifade eder.  "ε" madde cinsine bağlıdır. Eğer cisim 1.0 yani maksimum ışıma gücüne sahipse, bu cisim kara cisim ışıyıcısıdır. Kara cisim ışıyıcısı ideal bir sınırı temsil eder ve doğada görülmez. Bağıntıdaki  T ise Kelvin cinsinden sıcaklıktır.
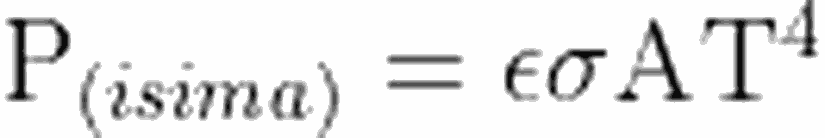
Formülü yorumlayacak olursak, mutlak sıfır (0 Kelvin) sıcaklığında bulunan cisimler ışıma yapmaz. Lakin sıcaklığı 0 Kelvin'den yüksek olan cisimler, (ben, sen, o, biz, siz, onlar...) termal ışıma yapar.  Tabii  cisimler termal ışıma yapmanın yanında, bu termal ışımayı bir de soğururlar.
Bir cismin T (çevre) sıcaklığında, çevresinden termal ışıma yoluyla soğurduğu enerjiyi şu şekilde ifade edebiliriz:

Bu iki bağıntının da bizlere gösterdiği gibi, cisimler düşük sıcaklıklarda da ışıma yaparlar. Yaptıkları bu ışıma gözle görülür alanın dışında ve  uzun dalga boyundadır. Cismin sahip olduğu sıcaklık arttıkça, cisim kızarmaya, başka deyişle yaptığı ışımanın dalga boyu azalmaya başlar (enerjisi artar).

Buraya kadar her şey normal ilerliyordu. Ancak fizikçiler, siyah bir cisim tarafından yapılan ışımanındalga boyu dağılımını incelemeye çalıştıklarında, duvara toslamışlardı. Buna geçmeden önce, bütünlüğü sağlamak adına, yukarıda bahsetttiğimiz kara cisim hakkında biraz daha bilgi verelim.
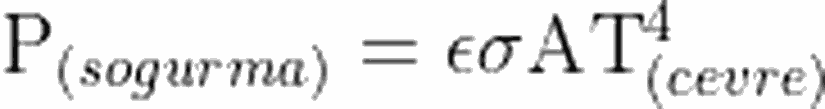
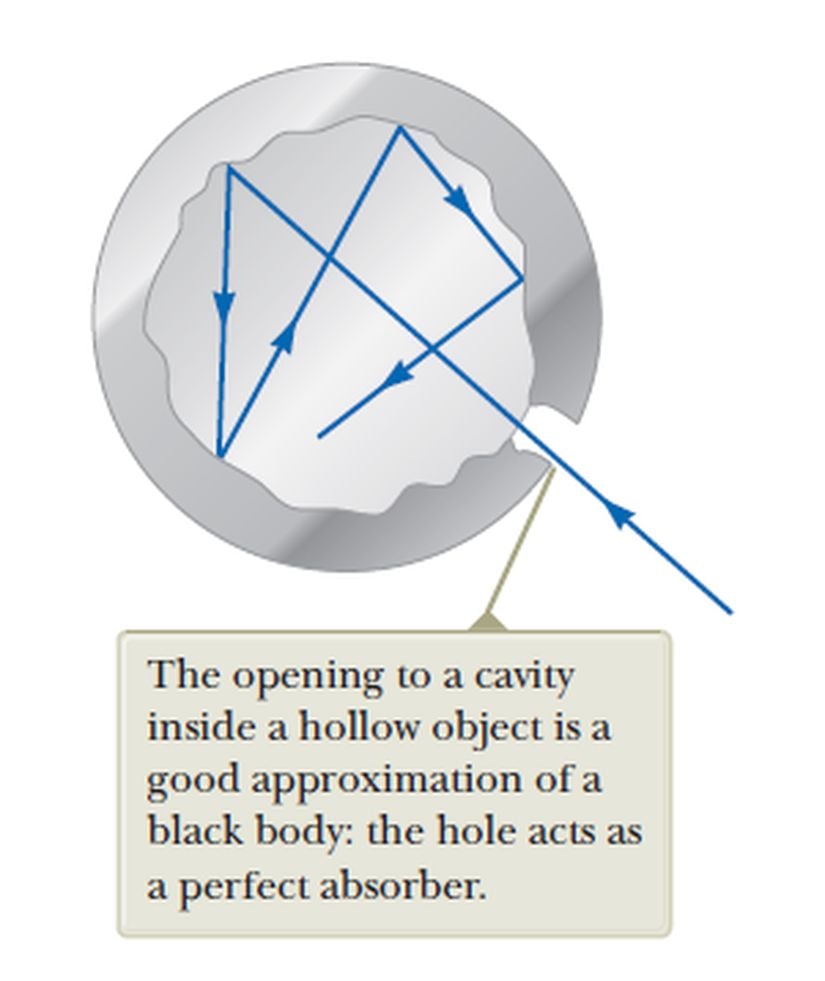
Kara cisim, yukarıda da bahsettiğimiz gibi, çok yüksek bir ışıma gücüne sahiptir. Yine yukarıda değindiğimiz gibi, yaptığı ışımanın gücü, yalnızca cismin sıcaklığına bağlıdır.

 
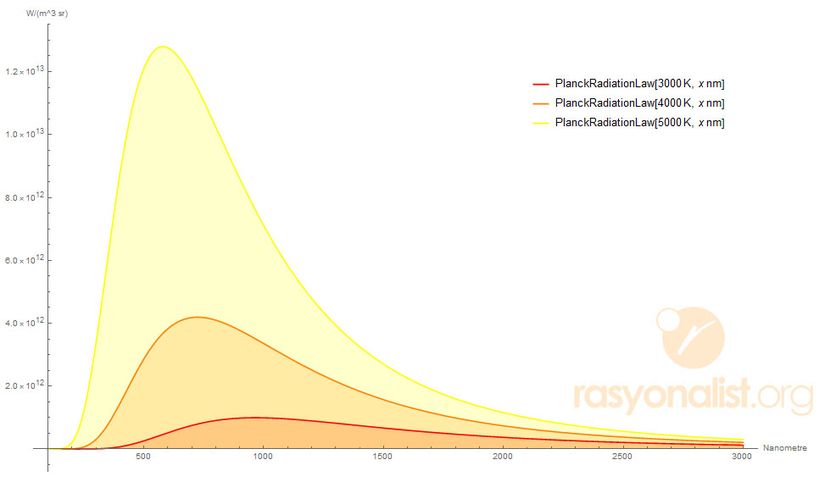
Yukarıda, bir kara cismin, belirli sıcaklıklarda yaptığı ışıma, dalga boyu (nanometre) cinsinden gösterilmiştir. Bu grafik bize şunları söyler:

1. Cisimler yalnızca sıcaklıklarına bağlı olarak bir termal (ısısal) ışıma yaparlar.
2. Bu ışıma, dalga boylarına göre farklı şiddetlerde olmak üzere bir dağılıma sahiptir. Fakat aynı şiddette ışıma, iki farklı dalga boyu tarafından yapılır, bu yüzden grafik dejeneredir.
3. Sıcaklık arttıkça, ışımanın maksimum yaptığı dalga boyu, yüksek enerjili dalga boylarına doğru kayma gösterir. Yani kabaca, soğuk bir cisim maksimum ışımasını kızılötede yaparken, sıcak bir cisim maksimum ışımasını morötede yapar.
4. Sıcaklık arttıkça, ışımanın maksimum yaptığı nokta yüksek enerjili bölgeye kayarken, aynı zamanda tüm dalga boylarında yaptığı ışıma artar. Yani sıcak bir cisim, soğuk cisime göre her bölgede daha fazla ışıma yapar, buna soğuk cismin maksimum yaptığı dalga boyu da dahildir.

(Konunun yıldız astrofiziğindeki yeri için ayrıca: Yıldız Astrofiziği Kara Cisim Işıması ve Wien Kayma Yasası'na göz atabilirsiniz.)
Klasik bakışa göre termal ışıma, cismin yüzeyine yakın atomlardaki yüklü parçacıkların ivmeli hareketlerinden kaynaklanır. Klasik bakışa dayalı olarak ortaya atılan Rayleight-Jeans yasası da, T ile orantılı bu hareketlilerin, hareketli başına ortalama enerjisini verir. Rayleight-Jeans yasası aşağıdaki gibi ifade edilebilir:

 
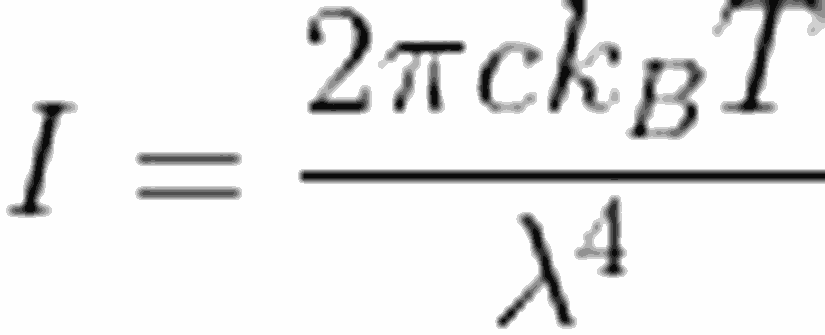
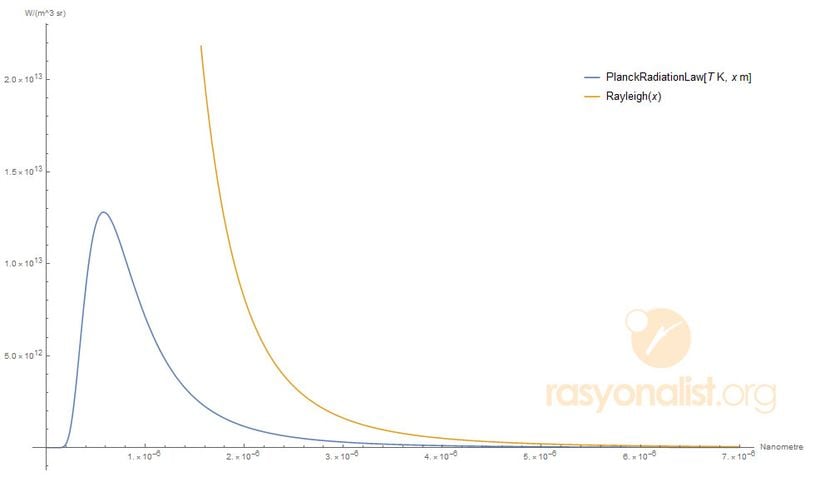
İşte, yukarıda bahsettiğimiz "Duvara toslama" da tam olarak burada oluyor. Uzun dalga boylarında bize deneysel verilerle oldukça uyumlu değerler veren bu bağıntı,kısa dalga boylarında bariz bir şekilde uyumsuzluk gösterir. λ 0'a yaklaşırken, yukarıdaki bağıntımızsonsuza yaklaşır. Deneysel veriler ise bize, dalga boyu 0'a yaklaştıkça,  I'nın da 0'a yaklaştığını gösterir. Süperkahramanımız Max Planck ortaya çıkmadan önce, bu çelişki bilim dünyasında öyle şaşırtıcı idi ki, bu çelişkiye "morötesi felaket" dediler.
Tüm bu çelişkilere son vermek adına, 1858 yılında Almanya'nın Kiel şehrinde bir süperkahraman doğdu. Max Planck 1900 yılında, cesur ve başarılı bir kuram ile,  tüm dalga boylarında deneylerle uyumlu olan bir bağıntı türetmeyi başardı.

Bu fonksiyon, Planck'a "süper kahraman" ünvanını kazandıran bir parametre içerir. "h" ile gösterilen bu parametre, temel bir doğa sabitir. Planck, kuramında iki cesur varsayımda bulundu.
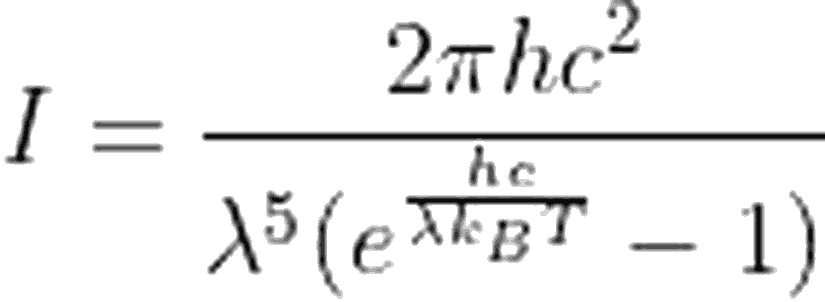
1- Moleküller yalnızca kesikli enerji değerlerine sahip olabilirler ve bu değerler

bağıntısıyla belirlenir. Bu bağıntıda n kuantım sayısı,f ise doğal titreşim frekanslarıdır. 
2- Moleküller kesitli paketler halinde enerji yayınlar ve soğururlar. Moleküller bir kuantum durumundan diğerine "atlayarak" bu fotonları yayınlar veya soğururlar.
Muhtemelen, 1. maddeyi okurken bazı okurlarımızın aklına Bohr Devrimi isimli yazımız gelmiştir. aslında, Planck'ın bile gerçekçi olduğunu düşünmediği kuantum kavramının başarılarından yalnızca bir tanesidir Bohr Devrimi.
1905 yılında Albert Einstein'ın, 1913 yılında Niels Bohr'un, 1924 yılında de Broglie'un çalışmaları, 1926 yılında adeta tüm bu bilgilerin bir sentezi olarak, modern fiziğin en temel taşlarından biri sayılan Schrödinger denklemleri, Planck'ın bağıntıları ve temel doğa sabiti olan Planck sabiti  ışığında ortaya koyuldu.

İleri Okuma

Planck dağılım fonksiyonunu aşağıdaki şekilde ifade edebiliyorduk.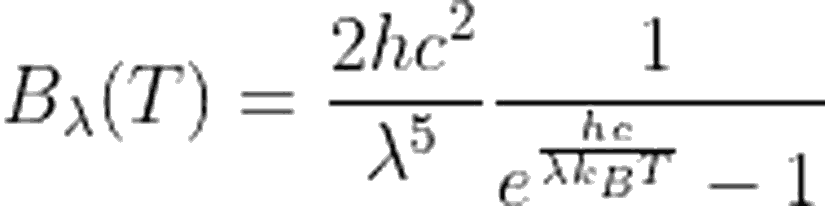

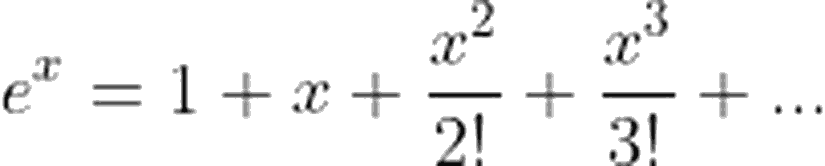
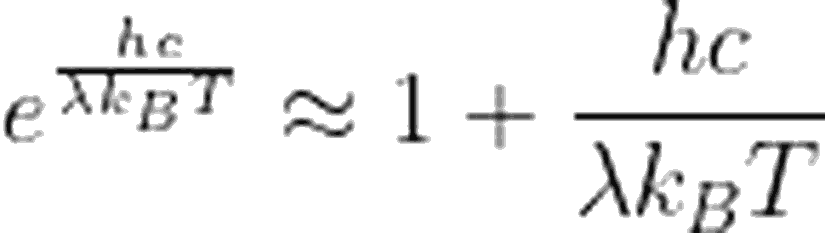
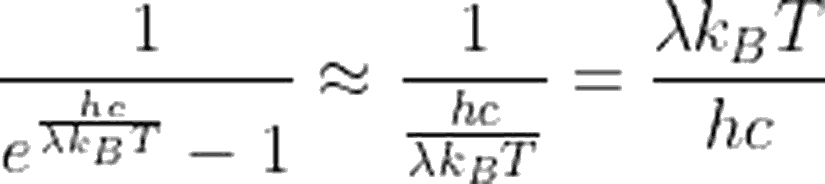
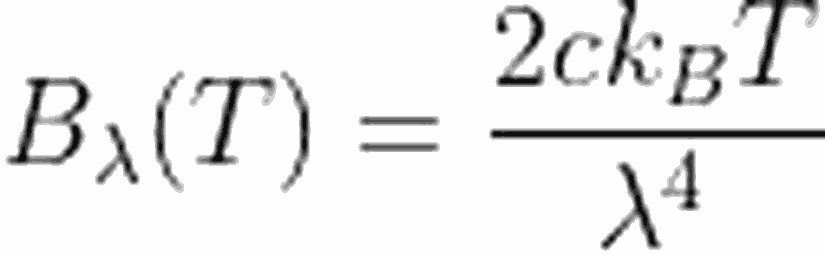
Figür 3'ten de gördüğümüz üzere, Planck dağılım fonksiyonu ile Rayleigh Yasası, uzun dalga boylarında benzerlik gösteriyor. Öyleyse uzun dalga boyları için yapacağımız açılımla, Planck dağılımının Rayleigh Yasası'nı vermesini bekleriz.

olduğundan, uzun dalga boylarında da eksponansiyelin çok küçüleceğini bildiğimizden, Taylor açılımının ilk terimini alarak bir yaklaşım yapabiliriz.

Bu durumda yukarıdaki ifadeyi aşağıdaki gibi düzenlersek

Sonunda ifadeyi düzenlediğimizde,

olarak bulunur, ki bu ifade Rayleigh Jeans Yasası'nın ta kendisidir. Fakat bu durumun, yalnızca uzun dalga boyları varsayımı altında olduğuna dikkat edin. Aksi takdirde, Taylor açılımında yaptığımız yaklaşım doğruluktan sapmaya başlayacaktır.
Aynı yaklaşım, frekansın fonksiyonu olarak verilen Planck dağılımı için de uygulanabilir. Uzun dalga boyu demek, düşük frekanslı dalgalar demek olduğundan yaklaşımımız $h\nu\ll k_B T$ olacaktır. Bu durumda,

olarak elde edilir.
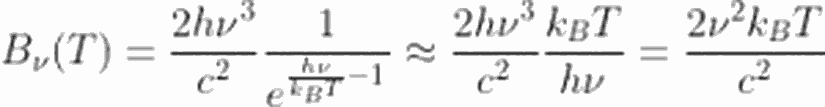
Hazırlayan: Ege Can Karanfil
Geliştiren: Ögetay Kayalı

---

Referanslar
1. David Griffiths, Introduction to Quantum Mechanics
2. Fevzi Köksal ve Rahmi Köseoğlu, Kuantum Mekaniği
3. Serway and Beichner, Fizik 3 (Modern Fizik) 5. Baskı
4. Halliday and Resnick, Fiziğin Temelleri, 1.Kitap, 9.Baskı
5. http://www.nobelprize.org/nobel_prizes/physics/laureates/1918/
6. http://galileo.phys.virginia.edu/classes/252/black_body_radiation.html
7. http://hyperphysics.phy-astr.gsu.edu/hbase/wien.html