Galvanometre Nedir, Ne Ölçer ve Nasıl Kullanılır?

Keskin ölçümler yapmak, bilim söz konusu olduğunda en önemli niteliklerden birisidir.Elektrik ve manyetizma söz konusu olduğunda da, galvanometreler tarihsel olarak son derece önemli ölçüm cihazlarıdır. Geçmişi 1870'lere kadar dayanan galvanometrelerin ilk örnekleri, Hans Christian Ørsted tarafından geliştirilmiştir. Galvanometreler, adını Luigi Galvani'den almaktadır.

Her ne kadar pek çok farklı amaç için farklı tasarımlar söz konusu olsa da, modern galvanometreler (döner bobinli galvanometreler) ise, Jacques-Arsène d'Arsonval tarafından 1881'de geliştirilen tasarıma sahiptir.

Galvanometre Nedir?

Galvanometreler, elektrik akımı taşıyan bir kablonun yanına yerleştirilen pusulanın iğnesinin sapması konseptinden esinlenilerek geliştirilen; bir devredeki akımı tespit etmek için kullanılan cihazlardır. Gerekli ekipmanlar yardımıyla, voltmetre ve ampermetre olarak kullanılabilirler.

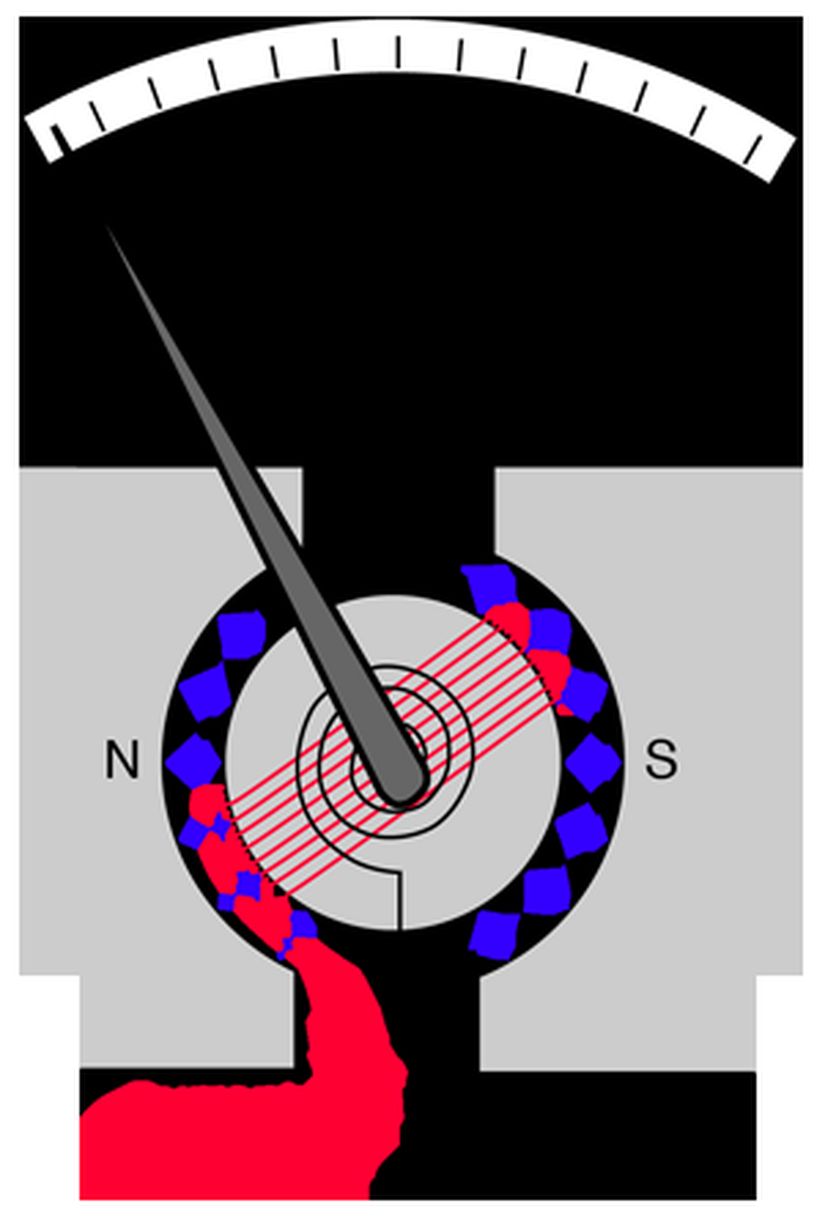
Galvanometre Nasıl Çalışır?

Döner bobinli galvanometreler, iki temel parçadan oluşmaktadır:

• Sabit bir merkez etrafında dönebilen, yüksek sayıda sargı içeren dikdörtgen şeklinde bir bobin
• Düzgün ve radyal manyetik alan oluşturan bir mıknatıs

Manyetik alan kuvvetini güçlendirmek için, sabit bir merkez etrafında dönebilen bir silindire, 1 numaralı figürde görüldüğü gibi sarılan bobin, düzgün ve radyal manyetik alanın içerisine yerleştirilir. Sarılı olan bobinden akım geçtiğinde, bobine etki eden manyetik alan sebebiyle tork oluşur. Oluşan bu torku dengelemek için, silindirin üzerine bir yay bağlanmıştır.

Bobinden geçen akım arttıkça, bobine etki eden tork da yükselir.

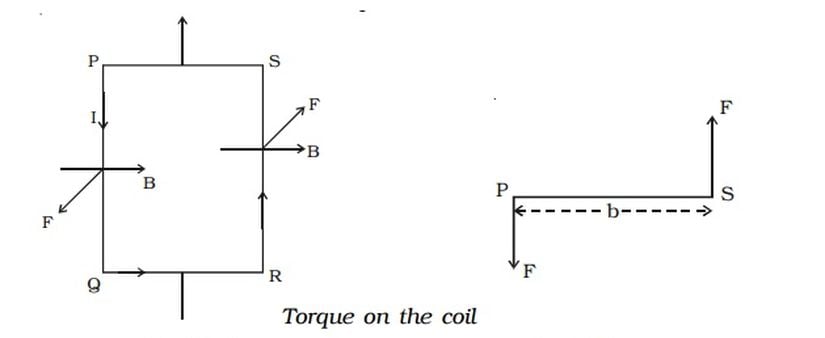
Hatırlayacak olursak, düzgün manyetik alan içerisindeki akım taşıyan tele etki eden kuvveti aşağıdaki gibi ifade edebiliyorduk:

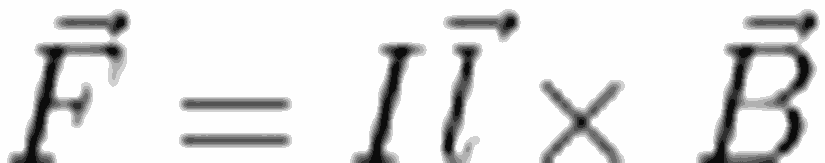
Öyleyse, 2 numaralı figürdeki bobinin RS ve PQ kısmına etki edecek olan kuvvetlerin, birbirine zıt yönlü olduğunu görebiliriz. Etki eden toplam kuvvet sıfır olsa bile, figürün sağında görebileceğimiz gibi, etki eden net tork, sıfırdan farklıdır. Tork ifadesi:

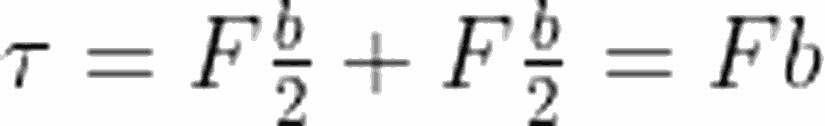
şeklindeydi. Dikkat edecek olursanız, ifadeleri skaler olarak yazdık. Bunun sebebi, vektör ifadeleriyle uğraşmayıp, uzun ve karışık matematikten kurtulmak (vektörel işlemler de bize aynı sonucu verecektir). Yukarıda bulduğumuz kuvvet ifadesini yerine yazacak olursak:

olur. Bu ifadedeki lb, dikdörtgen şeklindeki telin alanı (A) olduğu için, ifade:

halini alır. Sistemde bulunan yay, manyetik alan tarafından oluşturulan bu torku dengelediği için, herhangi bir denge anında, n sarıma sahip bobin için aşağıdaki ifadeyi yazabiliriz:

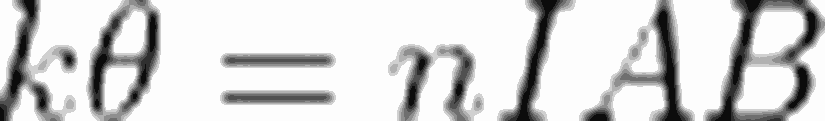
Burada Θ, denge konumundan sapmayı, k ise yay sabitini temsil eder. Sapma ne kadar yüksekse yani akım ne kadar fazlaysa, yayın bu sapmayı dengelemek için oluşturacağı tork da o kadar fazla olur. Yani:

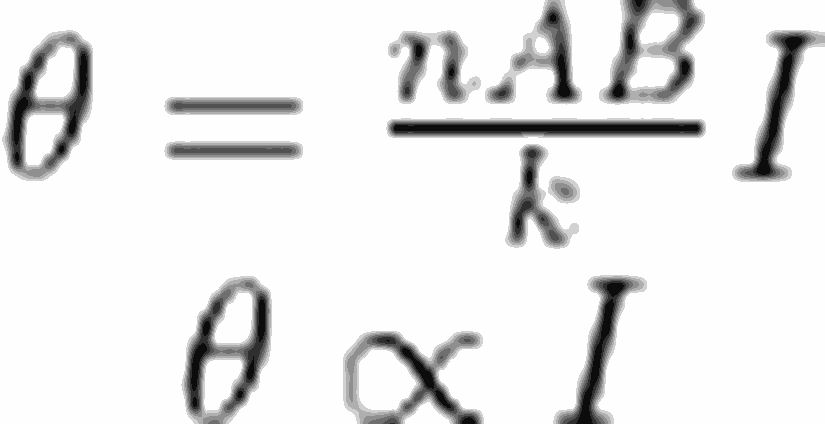
diyebiliz. Hatırlayacak olursanız, düzgün manyetik alanın radyal olduğunu söylemiştik. Manyetik alanın bu özelliği bize, bobine etki eden torkun, bobinin açısından bağımsız olmasını kazandırmaktadır (denklemde sinΘ ifadesi bulunmaz).

Galvanometrenin Kullanım Alanı

Yukarıdaki işlemlerden görebileceğimiz gibi, galvanometredeki sapma, üzerinden geçen akımla doğru orantılıdır. Bu özelliği, onunla çeşitli ölçümleri yapmamızı mümkün kılar.

• Düşük değere sahip bir dirence paralel bağlayarak, galvanometre yardımıyla akım ölçümü (ampermetre) yapabiliriz.
• Yüksek değere sahip bir dirence seri bağlayarak, galvanometre yardımıyla voltaj ölçümü (voltmetre) yapabiliriz.

Galvanometreden Ampermetre Yapımı

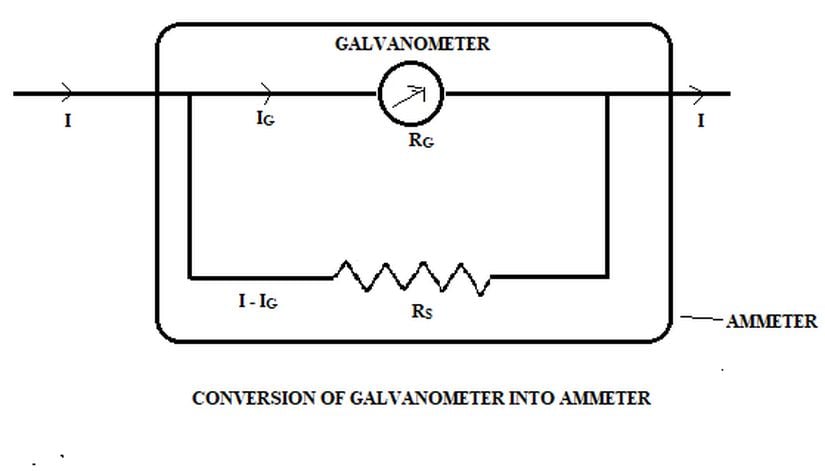
Yapacağı ölçüm aralığına uygun direnç galvanometreye paralel bağlayarak, galvanometremizi, bir ampermetre olarak kullanabiliriz. Paralel bağlı kollardaki potansiyel fark birbirine eşit olacağından, sisteme verilen toplam I akımı, için aşağıdaki eşitlik yazılabilir:

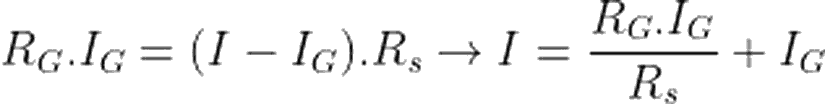
Eğer ki, galvanometrenizin kaç amperlik akımda maksimum sapmayı gösterdiğini ve ampermetrenin iç direncini biliyorsanız, yukarıdaki formül yardımıyla, istediğiniz aralıkta ölçüm yapabilen ampermetreyi oluşturabilirsiniz.

Örneğin, maksimum sapması 0.1A'de gerçekleşen ve iç direnci 50 Ω olan bir galvanometre ile, 1A'e kadar okuma yapmak için, Rs değerini hesaplayalım.

Rg değeri 50Ω, galvanometrenin sapmasının maksimum olduğu akım değeri 0.1 A olduğu için Ig değeri de 0.1A'dır. Öyleyse: 0.1A x50Ω=(1A-0.1A)xRs olduğundan, Rs değerini yaklaşık olarak 5.56 ohm olarak hesaplarız.

Galvanometreden Voltmetre Yapımı

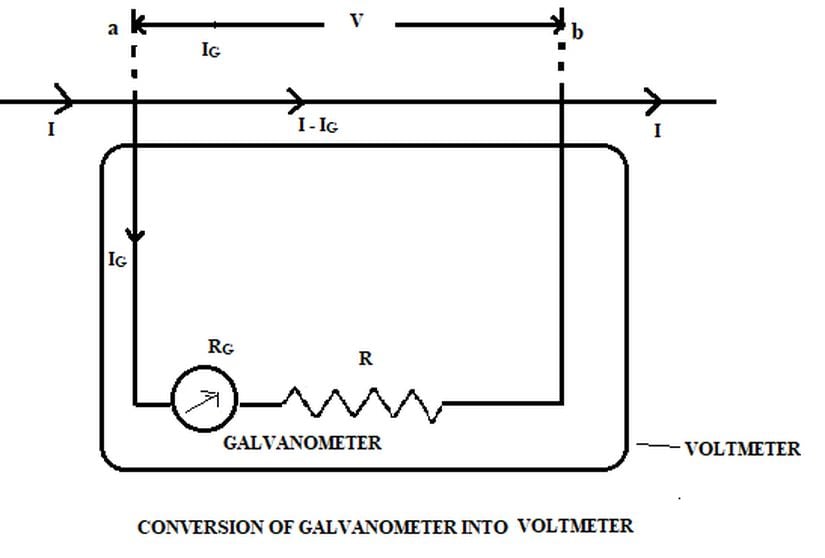
Ampermetreye benzer şekilde, iç direncini bildiğimiz galvanometremizi yapacağı ölçüm aralığına uygun dirence seri olarak bağlayarak, voltmetreyi oluşturabiliriz.

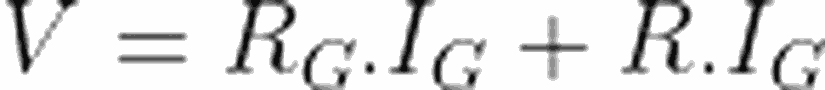
Voltmetrenin ölçeceği maksimum voltaj değerini (galvanometrenin maksimum sapmaya ulaşacağı değeri) belirledikten sonra, galvanometrenin maksimum sapmaya ulaştığı amper değerine o voltajda ulaşmak için gereken direnç, yukarıdaki eşitlikle kolaylıkla hesaplanabilir.

Benzer bir örneği de voltmetre için yapacak olursak, maksimum sapmayı 0.01A'da gösteren ve iç direnci 50 Ω olan galvanometremizin maksimum 5V ölçüm yapması için gereken R değeri, 5=50x0.01+Rx0.1'den, 45Ω olarak hesaplanır.

Hazırlayan: Ege Can Karanfil

Referanslar

1. Hyperphysics, "Galvanometer" <http://hyperphysics.phy-astr.gsu.edu/hbase/magnetic/galvan.html>

Agora Bilim Pazarı

TEK HİKAYE KİTAPLARI 1 RIFKI SERİSİ 5 KİTAP

Devamını Göster

₺250.00

Satın Al Tüm Ürünler

• Dış Sitelerde Paylaş

2. IOP, "From galvanometer to ammeter" <https://spark.iop.org/galvanometer-ammeter#gref>

3. Byju's, "Galvanometer" <https://byjus.com/jee/galvanometer/>

4. AboutCircuit, "Galvanometer" <https://www.aboutcircuit.com/galvanometer/>

5. Circuit Globe, "Galvanometer" <https://circuitglobe.com/galvanometer.html>

6. Serway ve Beichner, Fizik 2

7. Micheal E. Schultz, Grob's Basic Electronics, 12th Edition, Chapter 8

Görsel Referansları

1. http://www.brainkart.com/article/Torque-experienced-by-a-current-loop-in-a-uniform-magnetic-field_12097/

2. http://hyperphysics.phy-astr.gsu.edu/hbase/magnetic/galvan.html

3. https://en.wikipedia.org/wiki/Galvanometer

4.https://www.abc.net.au/science/articles/2010/07/07/2946773.htm