Özel Görelilik: İkizler Paradoksu & Eşzamanlılığın Göreliliği

- Özgün
İkizler Paradoksu
Dünya’da bulunan iki ikiz (ve dolayısıyla aynı yaşta) bir kardeş düşünün. Kardeşlerin isimleri Ali ve Ayşe olsun. Ayşe Dünya’dan uzak bir gezegene doğru ışık hızına yakın bir hızda seyahate çıksın, Ali ise Dünya’da kalmaya devam etsin. Ardından, Ayşe gezegene gidip, Dünya’da kalan Ali’nin yanına gelsin. Bu durumda Ayşe Dünya’ya döndüğü zaman kardeşlerin yaşları için ne söyleyebiliriz?Bu soruya her iki kardeşin gözlem çerçevesinden ayrı ayrı cevap vermeye çalışalım. Dünya’da kalan Ali’nin gözlem çerçevesinde Ayşe ışık hızına yakın bir hıza sahiptir, bu sebeple Ali’nin gözlem çerçevesinden Ayşe için zaman daha yavaş akar. Dolayısıyla Ayşe uzak gezegene gidip geldiğinde Ali daha yaşlı olacaktır.
Ayşe’nin gözlem çerçevesinden durumu incelediğimizde ise, kendisi durağanken Dünya ve Dünya’da kalan Ali’nin ışık hızına yakın bir hızı vardır. Dolayısıyla Ayşe’nin gözlem çerçevesinde kendisi için değil, Dünya’da kalan Ali için zaman daha yavaş akacaktır. Bu nedenle seyahatinden döndüğü zaman kendisi daha yaşlı olacaktır.
O halde sorumuz şu olur: Ayşe Dünya’ya döndüğünde Dünya’da kalan Ali’nin gözlem çerçevesinde kendisi daha yaşlı iken seyahat eden Ayşe’nin gözlem çerçevesinde kendisi daha yaşlıdır. Peki hangi ikiz haklıdır?
Kısa Çözüm
Dünya’da kalan Ali haklıdır. Bunun sebebini anlamak için göreliliğin temel iki varsayımına bakalım- Işığın vakumdaki hızı her eylemsiz gözlem çerçevesi için aynı değere sahiptir.
- Fizik yasaları her eylemsiz gözlem çerçevesi için aynıdır.
Verdiğimiz örnekte uzak gezegene gidip gelen Ayşe, eylemsiz bir gözlem çerçevesine sahip değildir çünkü ivmeleniyordur. İkiz Dünya’dan hareket ederken hızlanıyor ve gezegene inmek için ise yavaşlıyor. Bunların yanı sıra hız vektörel bir büyüklük olduğu için hızın değeri değişmeseydi bile yönü değiştiği için (çünkü ikiz gezegene gittikten sonra Dünya’ya dönmek için tersi istikamette gider) ivmenin varlığından söz edebiliriz. Özel görelilik eylemsiz gözlem çerçeveleri için geçerli olduğundan, olayları uzay gemisindeki ikizin gözlem çerçevesi açısından incelememiz yanlış olur. Ancak Dünya’da kalan ikiz eylemsiz olduğundan (Dünya’nın kendi etrafında ve Güneş’in etrafında dönüşünü ihmal ediyoruz) onun gözlem çerçevesinden olayları ele alabiliriz ve bu çerçeveden Dünya’da kalan ikizin kendisi daha yaşlıdır.
İvmesiz İkizler Paradoksu
Bu meşhur örneğin pek de bilinmeyen ama ilginç olan başka bir versiyonu vardır. İlginçtir çünkü ivmelenen bir gözlemci içermediği halde ortada bir paradoks ortaya çıkıyormuş gibi görünür. Bu versiyonda iki değil üç gözlemci bulunur, fakat bu hali biraz karmaşık olduğundan biz yine iki kardeşin olduğunu ve ivmelenmenin olmadığını kabul ederek, bunun farklı bir versiyonunu ele alacağız. Paradoksun üç kişilik versiyonunu izlemek isterseniz Brian Greene’in bu versiyonu açıkladığı videosunu aşağıdan izleyebilirsiniz.https://www.youtube.com/watch?v=AM41pweAVn0
Olay
Bir önceki örneğimizde olduğu gibi isimleri Ali ve Ayşe olan ikiz kardeş düşünelim. Fakat bu sefer Ali Dünya’da iken Ayşe 1 milyon 800 bin kilometre uzaklıkta bir gezegende olsun ve bir uzay aracıyla ışığın beşte üçü hızla Dünya’ya doğru gelsin. Ali’nin yanında Dünya üzerinde bulunan, bir saate bağlı ve düğmesi olan öyle bir bomba olsun ki bombaya bağlı saat başlatıldığı andan itibaren 10 saniye sonra düğmeye basılması durumunda bomba patlamasın. Fakat saatin başlatılmasından itibaren 10 saniyeden daha kısa bir sürede basılması durumunda bomba patlasın. Ayşe yolculuğuna başladığı anda Ali’nin, bombanın saatini başlattığını düşünelim. Sorumuz şu: Ayşe Dünya’ya varıp bombanın düğmesine bastığı zaman bomba patlar mı patlamaz mı? Bu soruya her iki gözlem çerçevesinden cevap vermeye çalışalım.Ali'nin Gözlem Çerçevesine Göre
Ali’nin gözlem çerçevesinde saatli bomba ile beraber Ali de Dünya’da olduğu için bomba da durağandır ama Ayşe 1 milyon 800 bin kilometre kadar yolu ışığın beşte üçü hızla kat etmektedir. Bu bilgileri göz önünde bulundurarak Ali’nin gözlem çerçevesinde Ayşe düğmeye bastığı zaman saatin kaç gösterdiğini hesaplayalım. Ayşe’nın hızını aşağıdaki şekilde gösterebiliriz.
Işığın hızının kabaca saniyede 300 bin kilometre olduğunu düşünürsek Ayşe’nin hızını metre/saniye cinsinden hesaplayabiliriz.
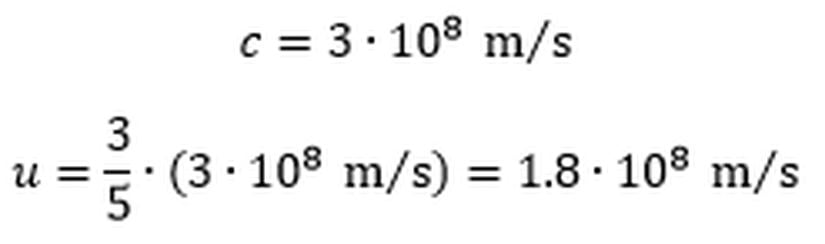
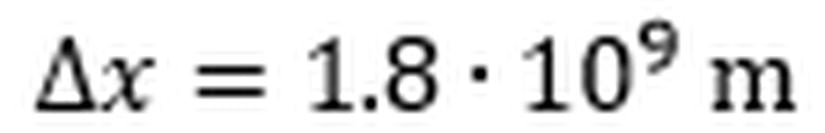

Ayşe'nin Gözlem Çerçevesine Göre
Ayşe’nin gözlem çerçevesinde kendisi durağandır ancak Dünya, Ali ve saatli bomba kendisine doğru ışık hızının beşte üçü değerinde yol kat etmektedir ve bu nedenle bombanın saati daha yavaş ilerler. Üstelik bunun yanı sıra kendisi ve Dünya arasında ölçtüğü uzaklık Ali’nin ölçtüğünden daha azdır, bunun sebebi Lorentz kısalmasıdır. Dolayısıyla Ali’nin gözlem çerçevesinden sonra Ayşe’nin gözlem çerçevesinden hesaplamaya kalktığımız durumda iki şey değişir:- Bombanın saati daha yavaş ilerler. (Zaman Genleşmesi)
- Dünya ve Ayşe arasındaki uzaklık daha kısadır. (Lorentz Kısalması)
Öncelikle Lorentz faktörünü hesaplayalım
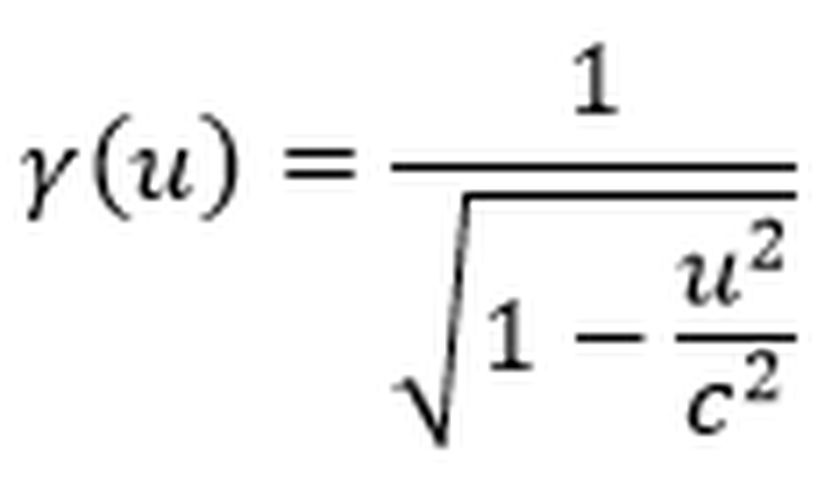
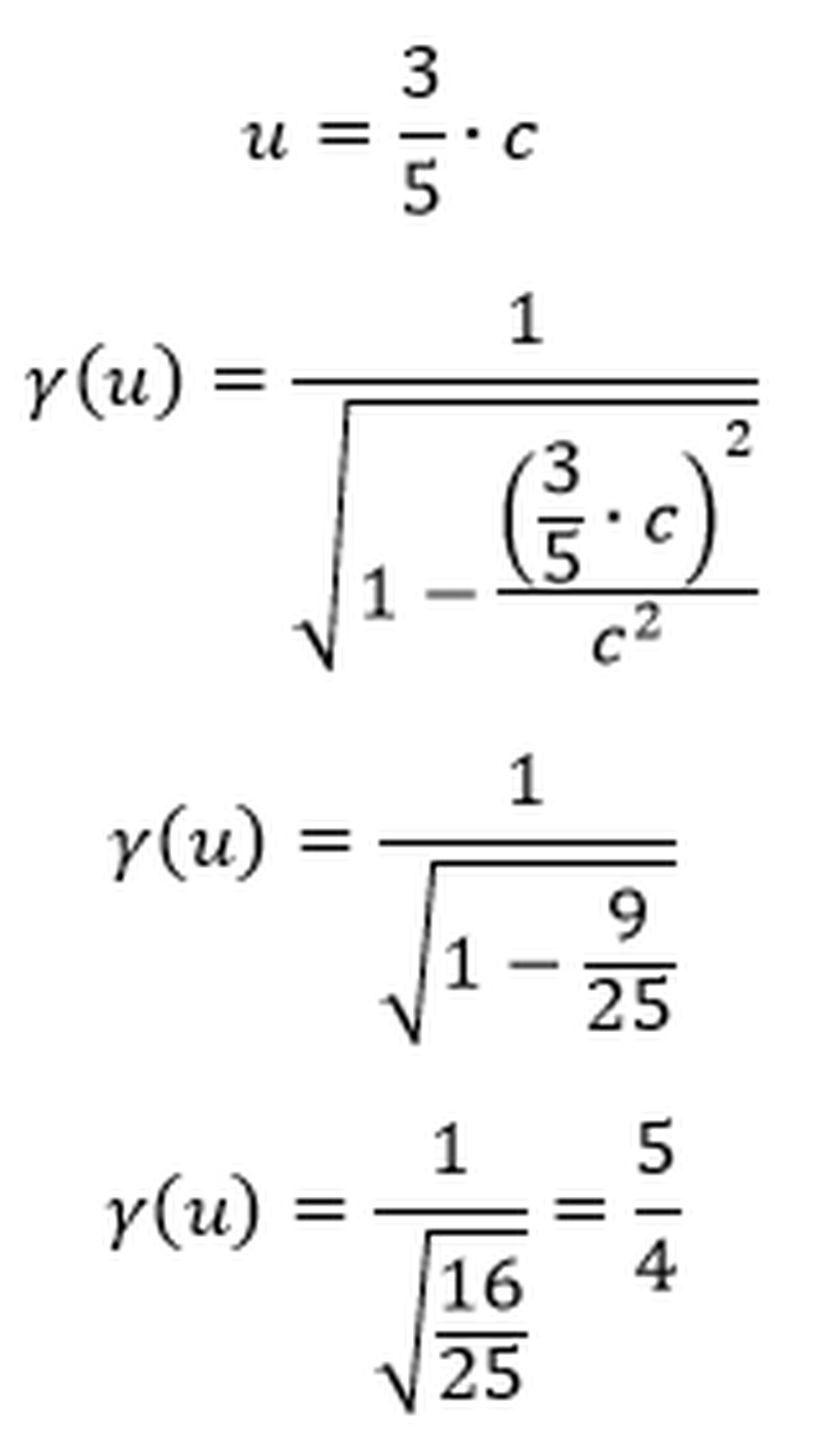
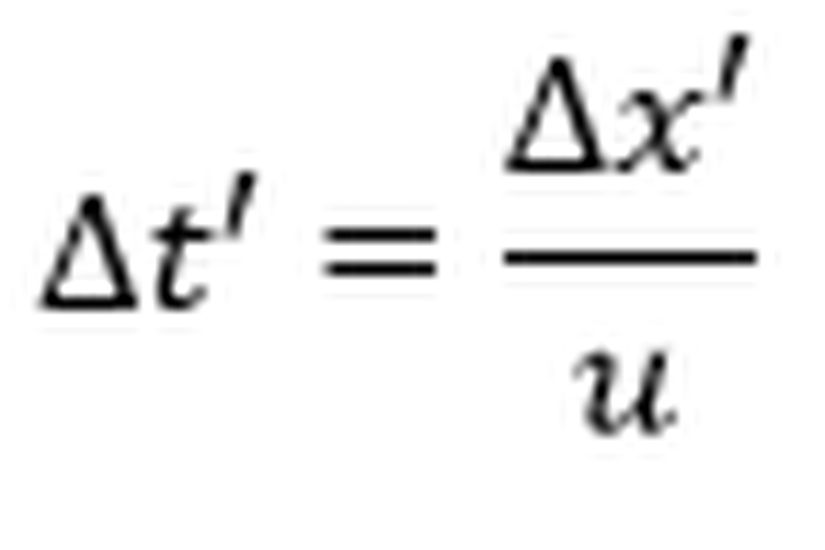
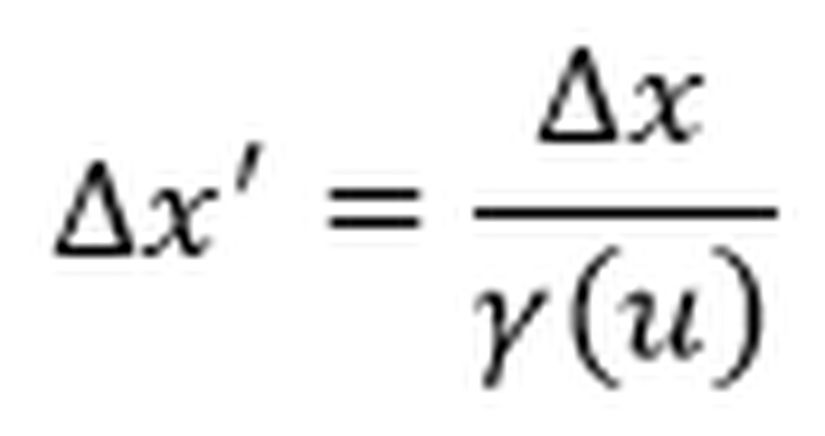
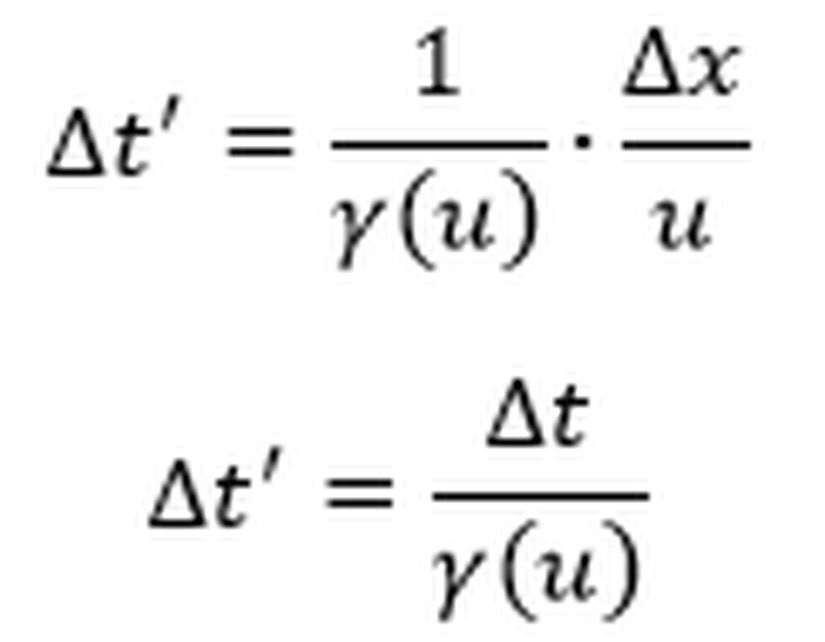
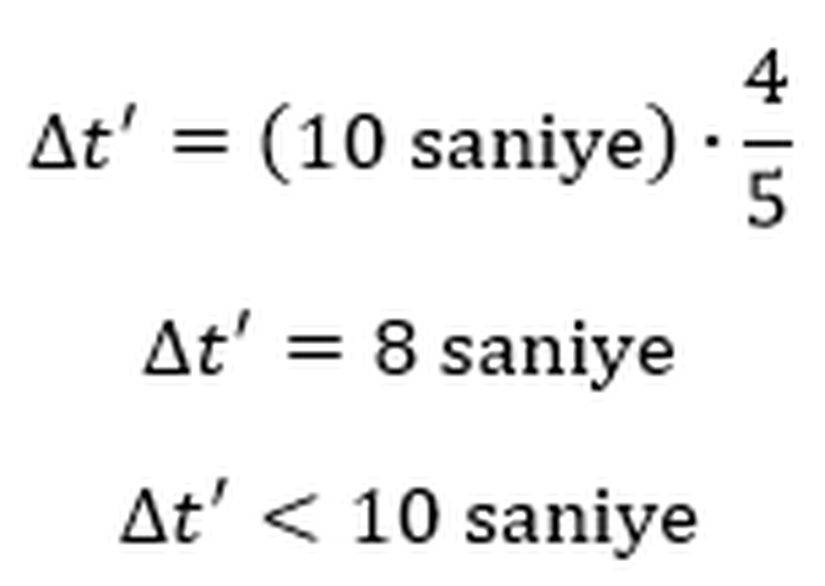
Paradoksumuz ortaya çıkmıştır. Ali’nin gözlem çerçevesinde bomba etkisiz kalırken, Ayşe’nin gözlem çerçevesinde bomba patlıyordur. Peki hangi gözlemci haklıdır?
Kısa Çözüm
Eşzamanlılığın göreliliğinin hesaba katılmayışı burada da sorun çıkartmıştır. Şöyle ki; örneğimizde Ali’nin bombanın saatini başlatması ile Ayşe’nin gezegenden yolculuğa çıkmasının aynı anda olduğunu söyledik. Ancak aynı anda ifadesini söylerken hangi gözlem çerçevesinde aynı anda olduğunu belirtmemiz gerekirdi. Varsayalım ki Dünya’da olan Ali’nin gözlem çerçevesinden saati başlatması ile Ayşe’nin yola çıkması aynı anda olsun. Bu durumda Ayşe’nin gözlem çerçevesinden yola çıktığı zaman Ali’nin saati çoktan başlatmıştır, yani saatin başlamasından itibaren bir süre çoktan geçmiştir. Dolayısıyla Ayşe’nin gözlem çerçevesinden, Ayşe’nin yola çıkmaya başlaması ile düğmeye basması arasındaki zamansal fark, Ali’nin ölçtüğünden daha az olsa da Ayşe saatin düğmesine bastığı zaman saatin gösterdiği değer her iki gözlem çerçevesinde aynıdır.Cevabı anlamak adına şöyle düşünebilirsiniz: Ali’nin gözlem çerçevesinde Ayşe gezegenden ayrıldığında saat de aynı anda başladığı için 0 saniyeyi gösteriyor ve 10 saniye sonra Ayşe Dünya’ya varıp bombanın düğmesine bastığı zaman 10 saniyeyi gösteriyor. Ayşe’nin gözlem çerçevesinden ise gezegenden ayrıldığında Dünya’da bulunan saat 2 saniyeyi gösteriyor (bu değerin nasıl elde edildiği uzun çözümümüzde anlatılmıştır) ve Ayşe 8 saniye sonra Dünya’ya vardığı zaman saat aynı şekilde yine 10 saniyeyi gösteriyor. Dolayısıyla Ayşe için gezegenden Dünya’ya gidiş süresi daha kısa olsa bile her iki gözlem çerçevesinde de Ayşe düğmeye bastığı zaman bombanın saati 10 saniyeyi gösteriyor. Ayşe’nin gözlem çerçevesinden yolculuğa çıkmasını ve bombanın saatinin başlatılmasının aynı anda olduğunu varsaysaydık her iki gözlemci için de Ayşe düğmeye bastığı an saat 8 saniyeyi gösteriyor ve dolayısıyla her iki gözlemci için de bomba patlıyor olacaktı.
Uzun Çözüm
Örneğin paradoks gibi görünen kısmını açıkladığımıza göre daha matematiksel kısmına geçebiliriz. Dünya’da olan Ali’nin gözlem çerçevesinden uzay-zaman diyagramı şöyle görünür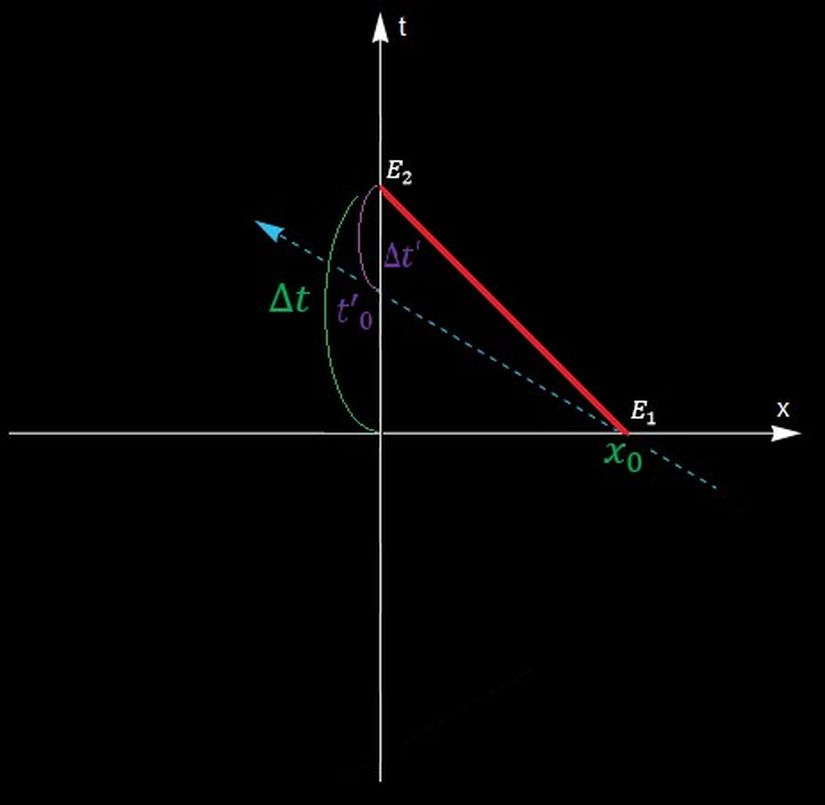
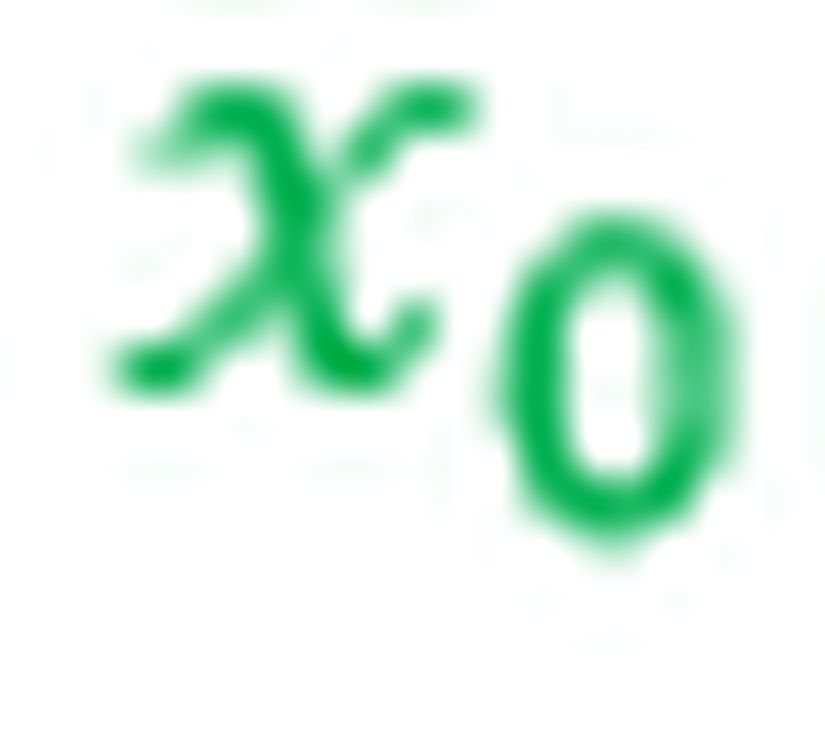
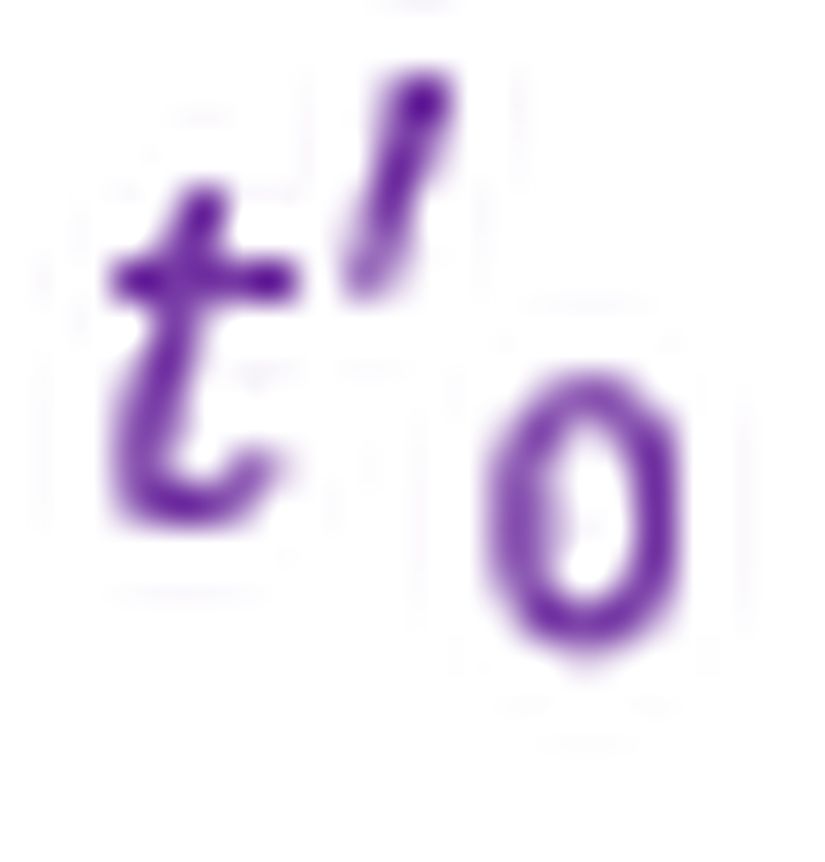


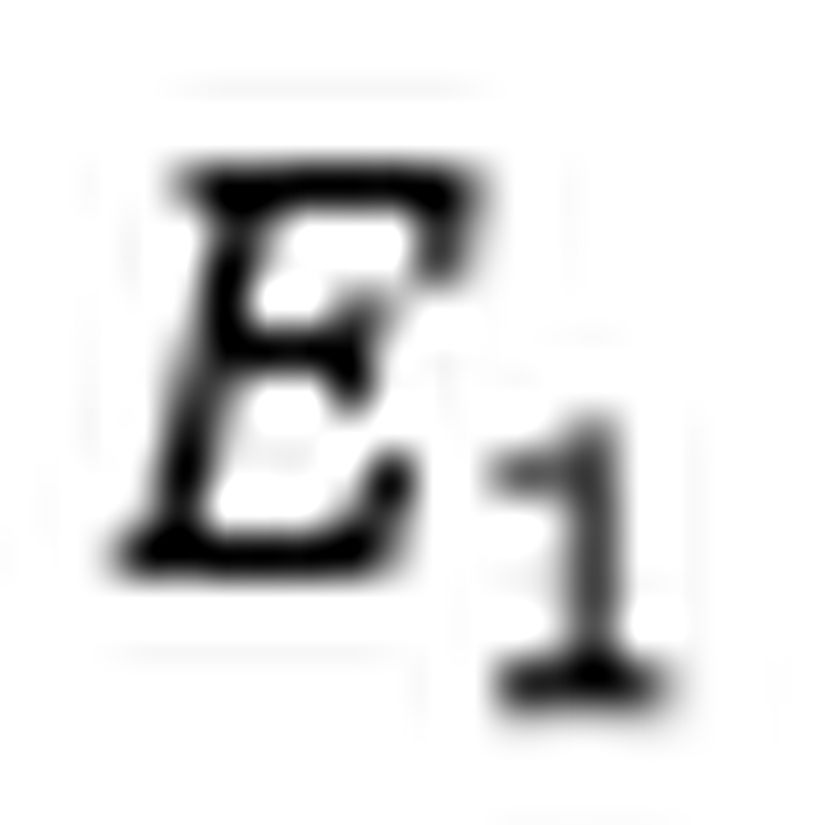
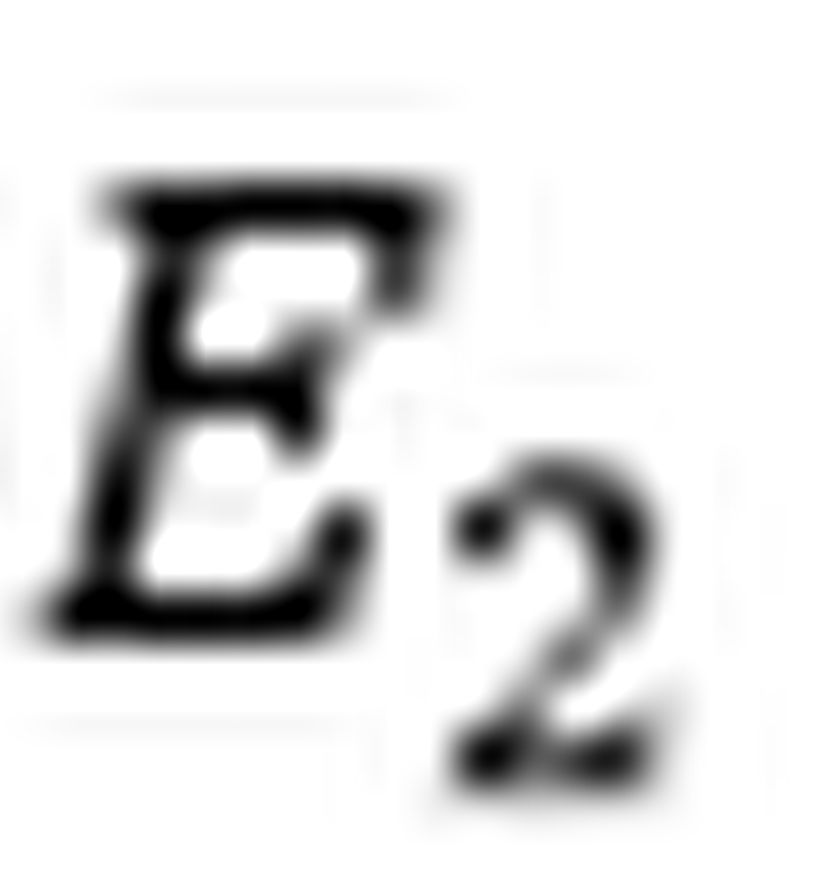
Öncelikle şunu belirtmemiz gerekir ki bu olayın matematiksel bir izahını verebilmek için Lorentz dönüşümlerini daha farklı şekilde formüle etmeliyiz çünkü Lorentz dönüşümleri durağan gözlemcinin zaman ve uzay koordinatlarında bulunurken
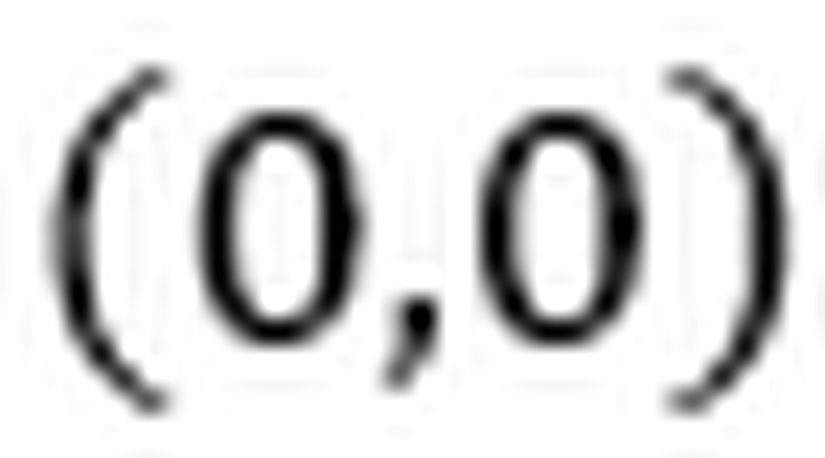
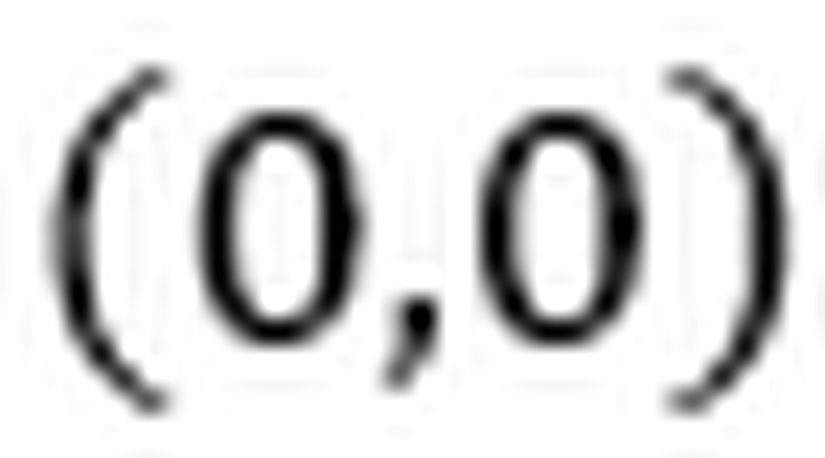
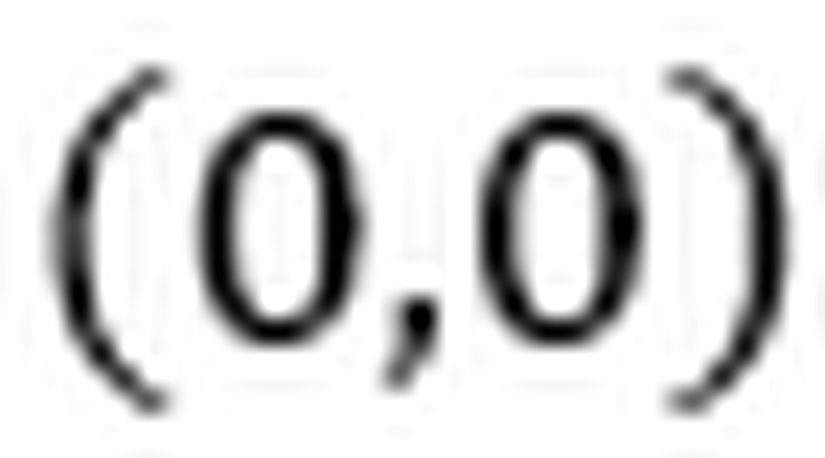
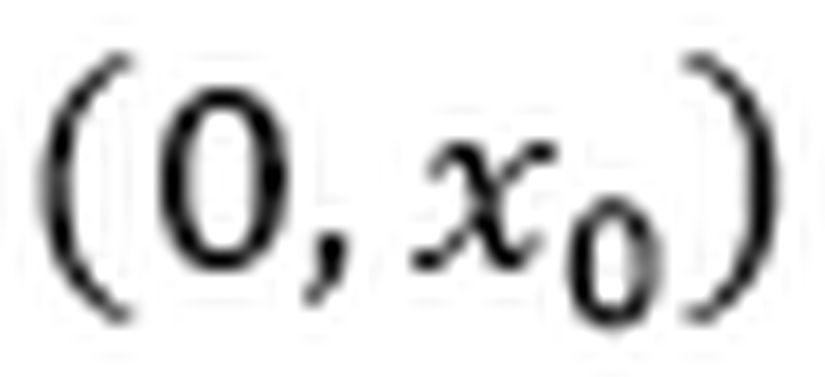
Lorentz Dönüşümleri’ni türetmenin pek çok yolu vardır fakat matematiği olabildiğince kolay tutmak adına Brian Greene’nin aşağıdaki videolarda türettiği şekilde türeteceğiz. Brian Greene’nin nasıl türettiğini görmek için aşağıdaki linklere tıklayabilirsiniz.Yazıyı uzatmamak adına Lorentz Dönüşümleri’nin bilinen halini tekrar türetmek yerine örneğimiz için uygun versiyonunu türeteceğiz.
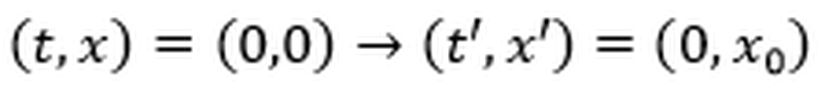
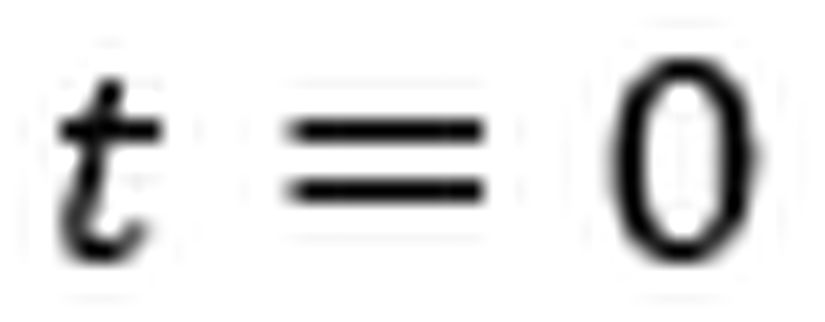
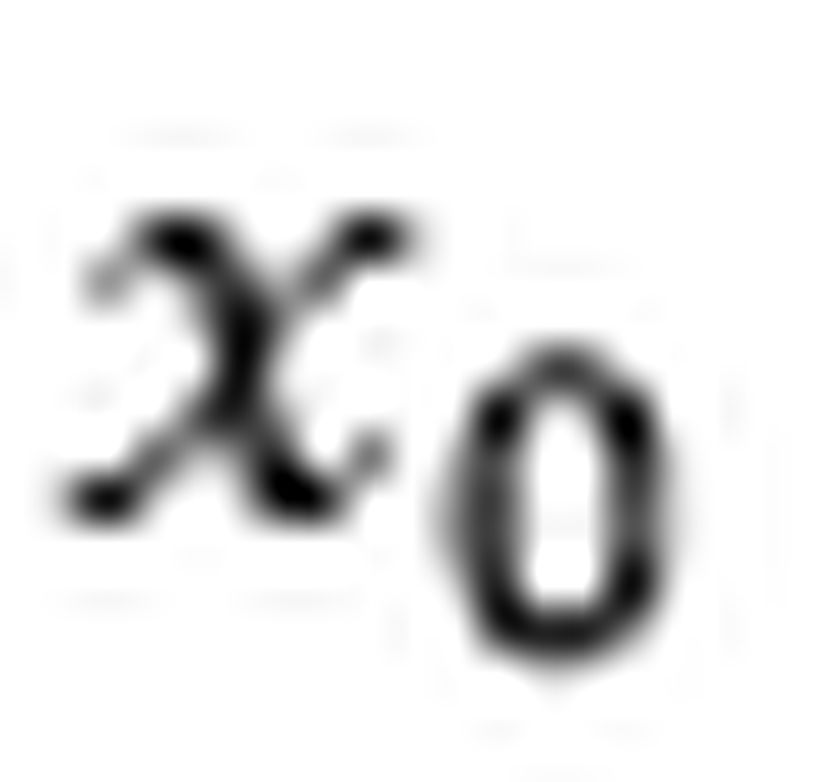
Aslında maddi destek istememizin nedeni çok basit: Çünkü Evrim Ağacı, bizim tek mesleğimiz, tek gelir kaynağımız. Birçoklarının aksine bizler, sosyal medyada gördüğünüz makale ve videolarımızı hobi olarak, mesleğimizden arta kalan zamanlarda yapmıyoruz. Dolayısıyla bu işi sürdürebilmek için gelir elde etmemiz gerekiyor.
Bunda elbette ki hiçbir sakınca yok; kimin, ne şartlar altında yayın yapmayı seçtiği büyük oranda bir tercih meselesi. Ne var ki biz, eğer ana mesleklerimizi icra edecek olursak (yani kendi mesleğimiz doğrultusunda bir iş sahibi olursak) Evrim Ağacı'na zaman ayıramayacağımızı, ayakta tutamayacağımızı biliyoruz. Çünkü az sonra detaylarını vereceğimiz üzere, Evrim Ağacı sosyal medyada denk geldiğiniz makale ve videolardan çok daha büyük, kapsamlı ve aşırı zaman alan bir bilim platformu projesi. Bu nedenle bizler, meslek olarak Evrim Ağacı'nı seçtik.
Eğer hem Evrim Ağacı'ndan hayatımızı idame ettirecek, mesleklerimizi bırakmayı en azından kısmen meşrulaştıracak ve mantıklı kılacak kadar bir gelir kaynağı elde edemezsek, mecburen Evrim Ağacı'nı bırakıp, kendi mesleklerimize döneceğiz. Ama bunu istemiyoruz ve bu nedenle didiniyoruz.
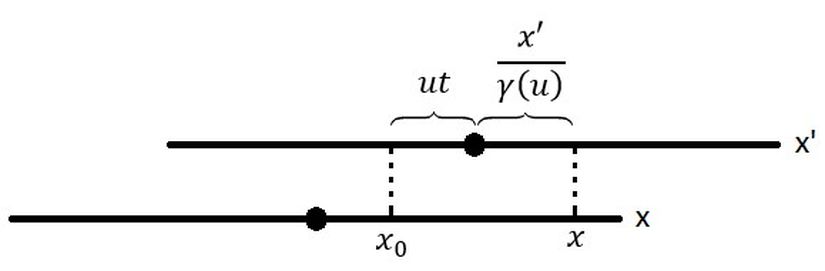
Hareketli gözlemci
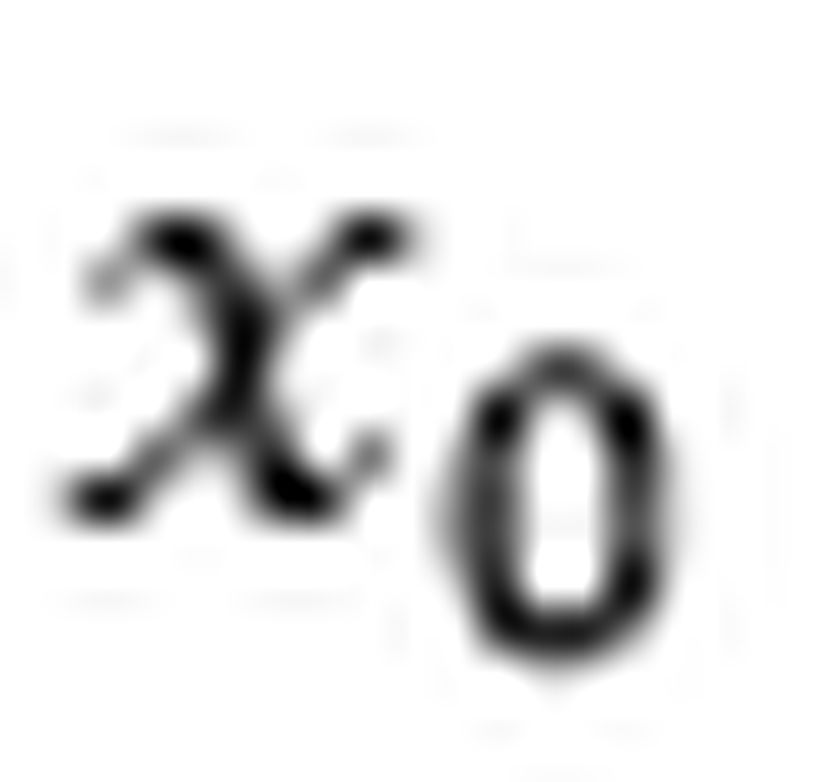
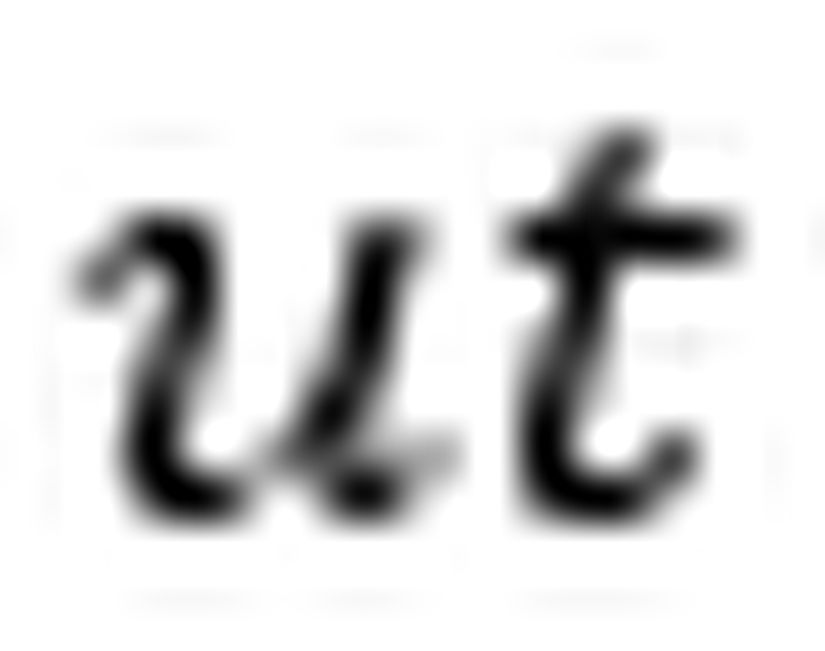
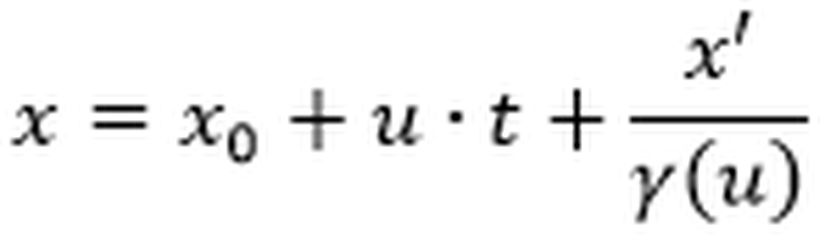
Yukarıdaki resmi bir de hareketli gözlemcinin gözünden bakmak istersek elde edeceğimiz resim şu şekilde olur.
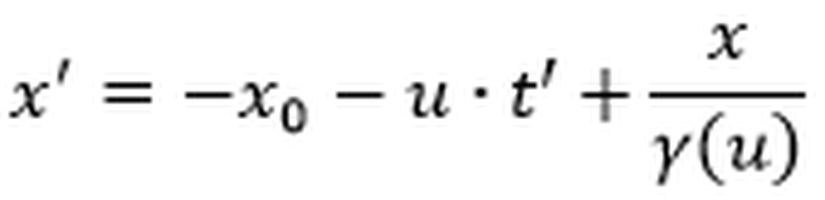
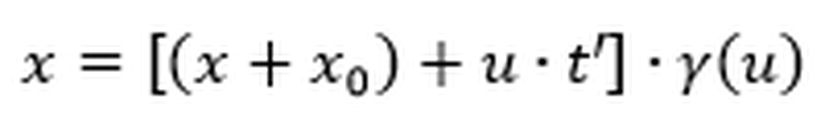
Fark edebileceğiniz üzere eğer
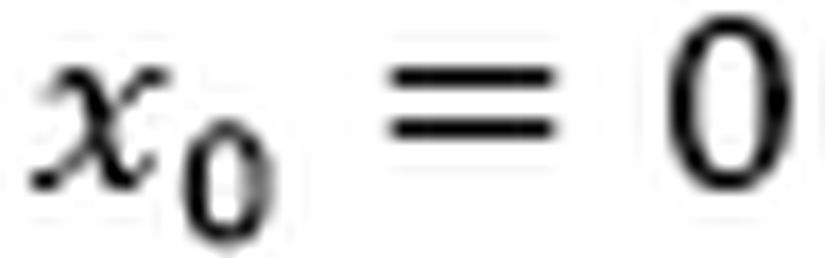
Yapacağımız diğer bir işlem ise yukarıda türettiğimiz yeni dönüşümlerde u gördüğümüz yere -u yazmak olacak. Bunun sebebi yukarda formülleri türetirken durağan gözlemcinin gözlem çerçevesinden hareketli gözlemcinin +x yönüne doğru gittiğini varsaymamızdır ancak çözümün başında verdiğimiz diyagrama göre hareketli gözlemci –x yönüne doğru gidiyordur. Dolayısıyla onun hızını da -u olarak göstermemiz gerekecektir.

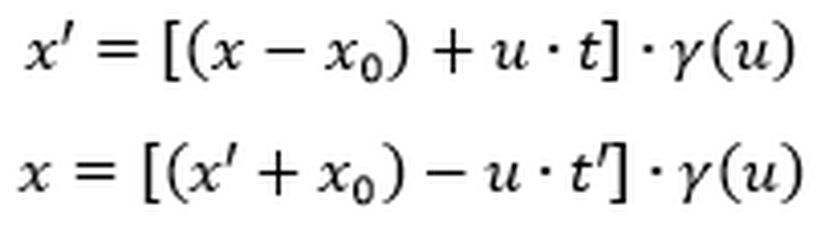
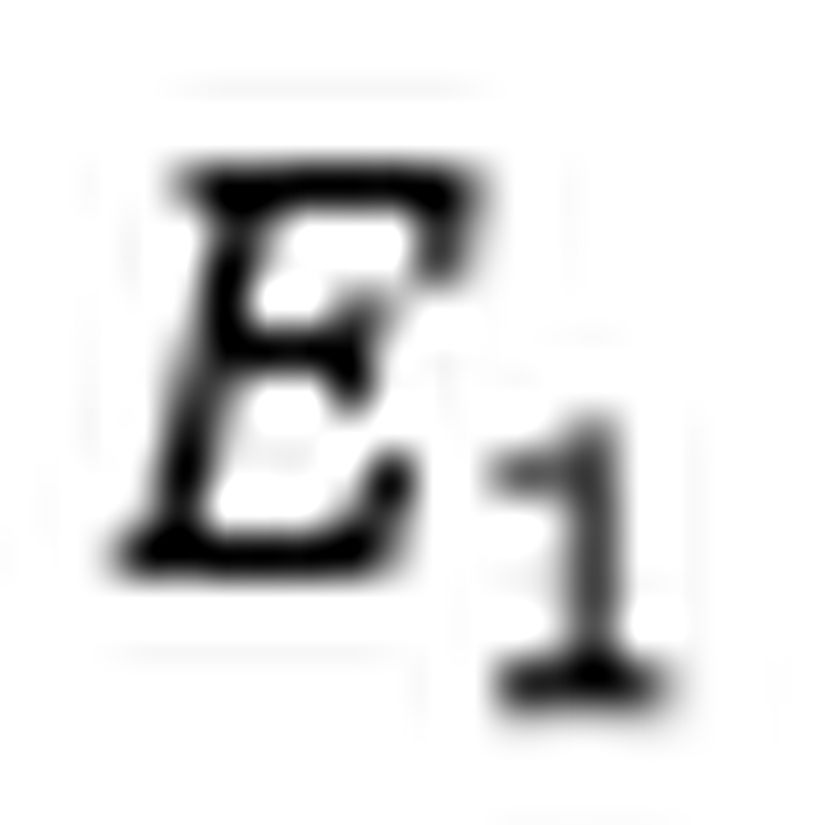
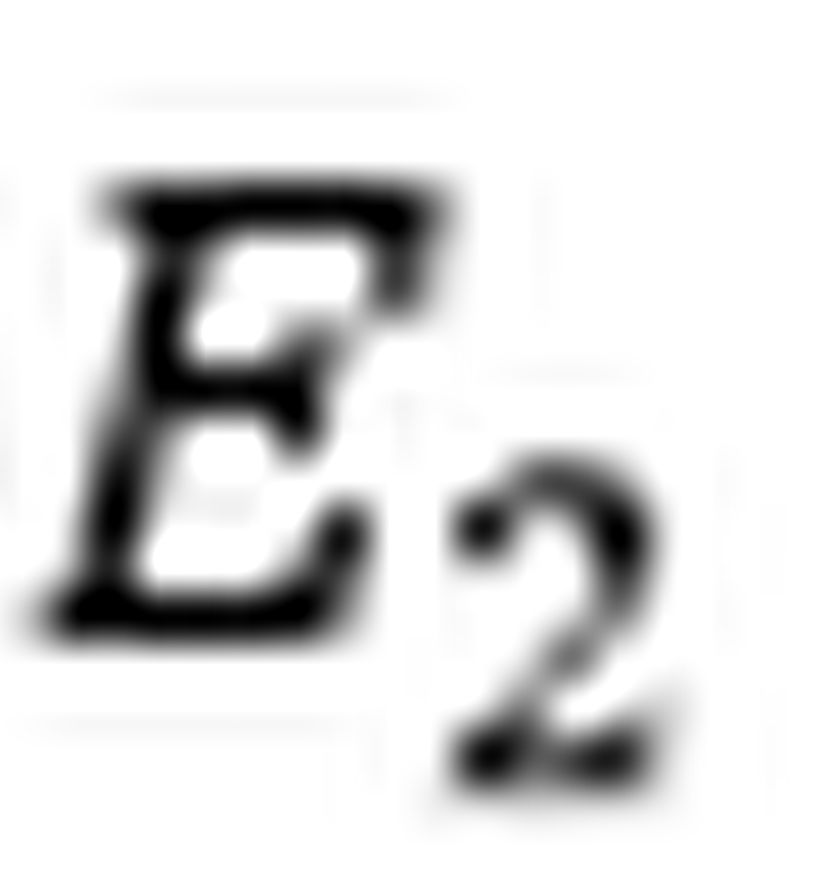
İlk olarak
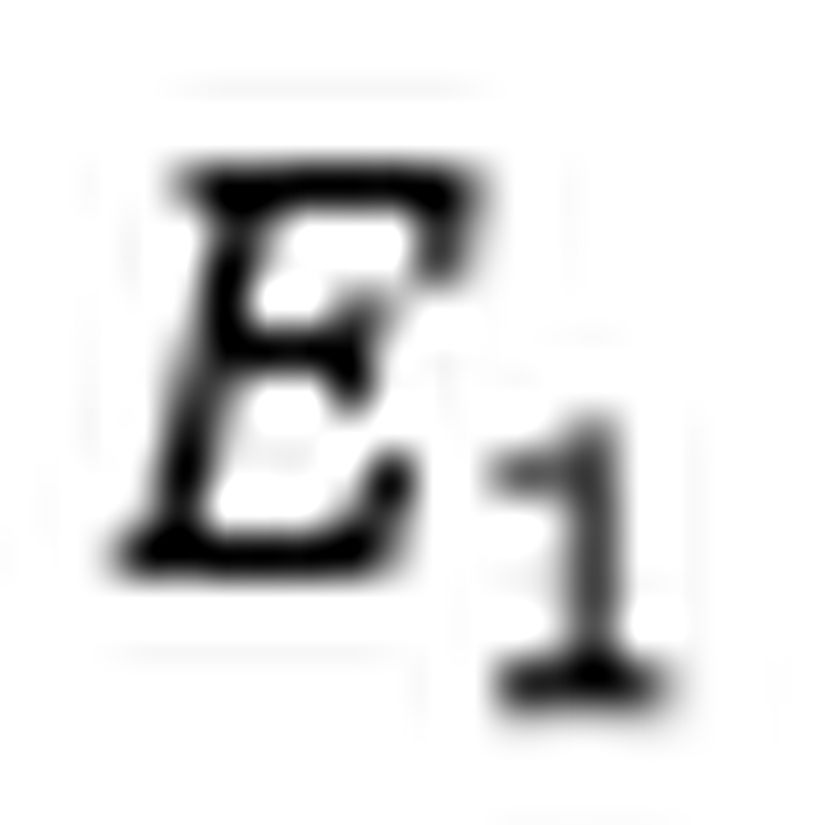
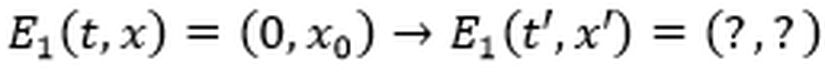
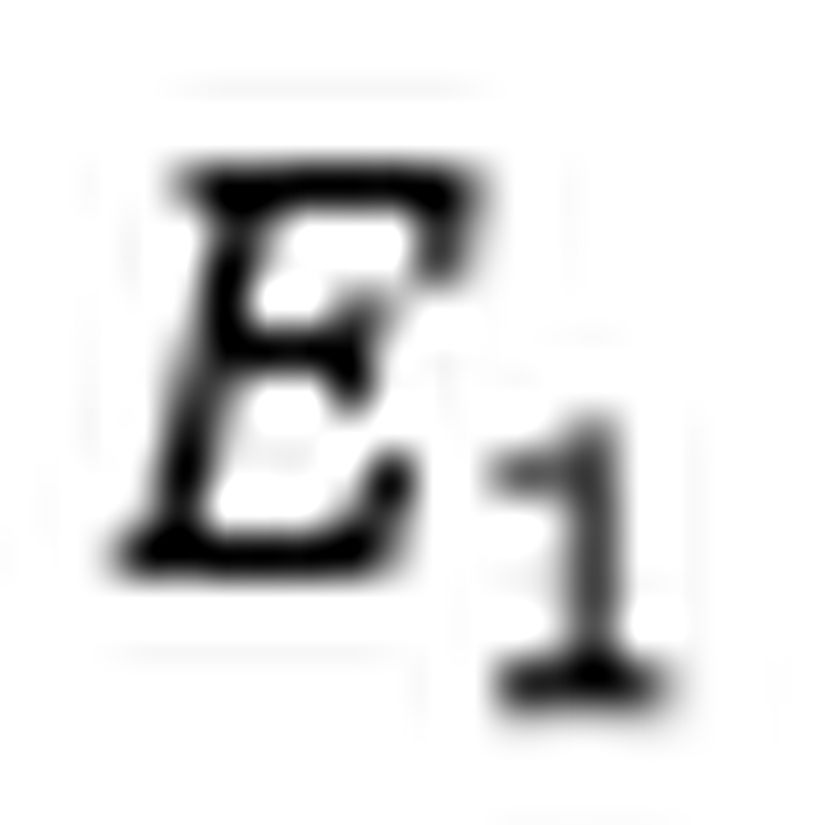
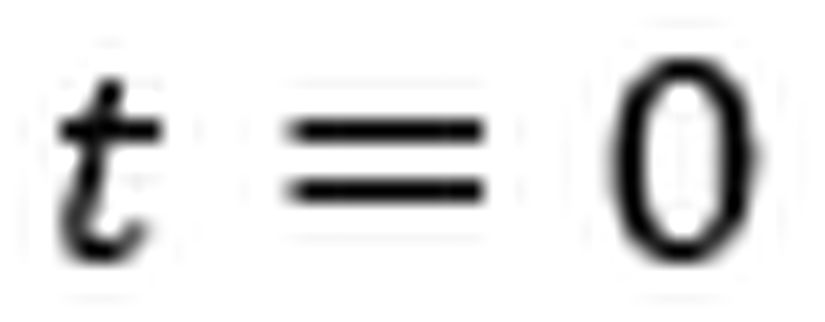
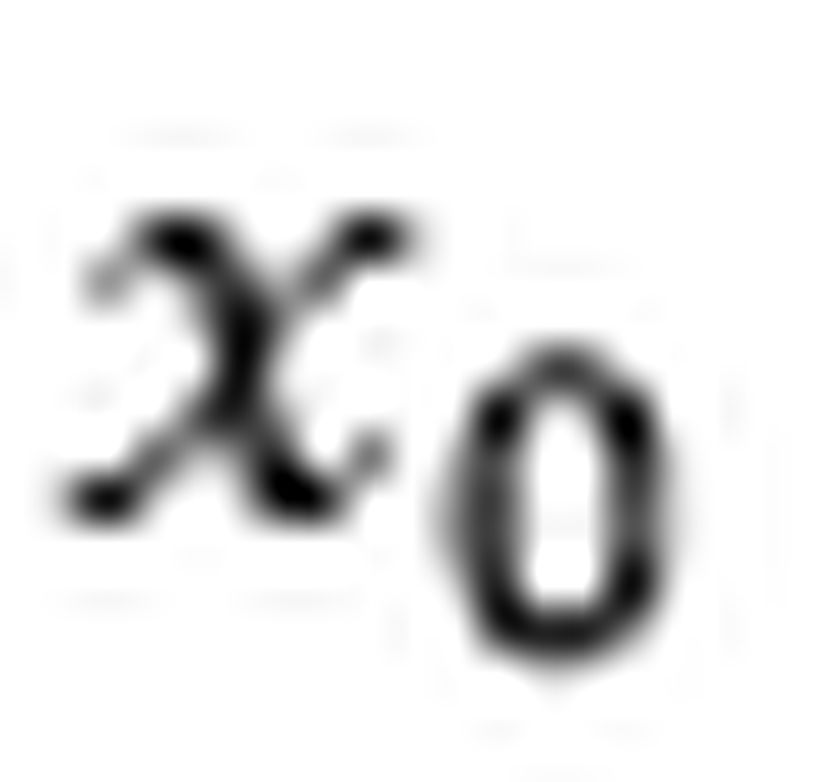
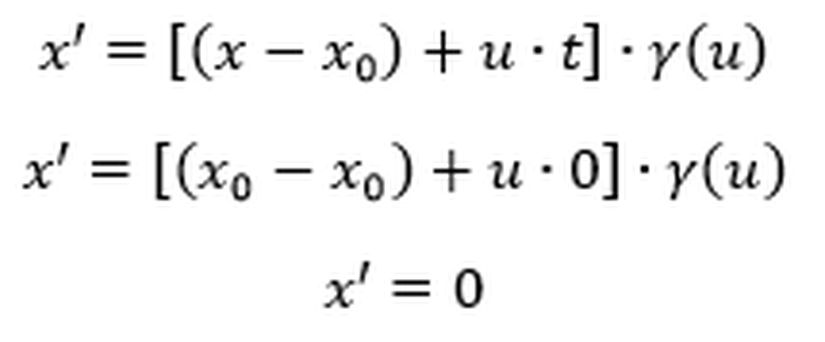
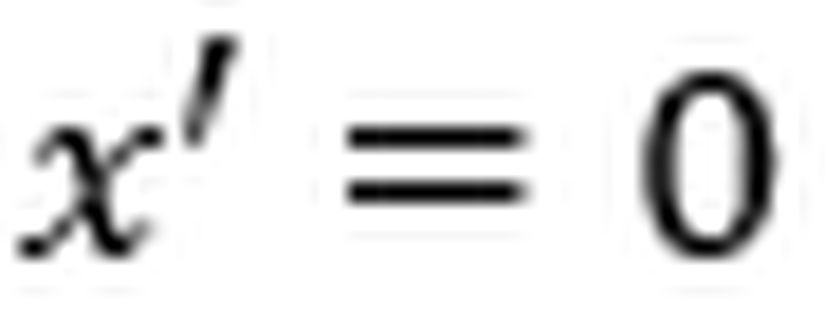
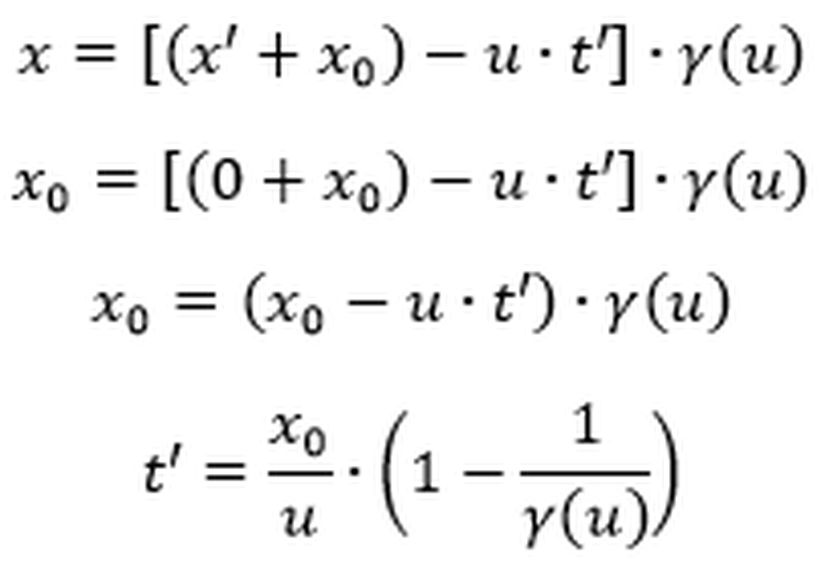
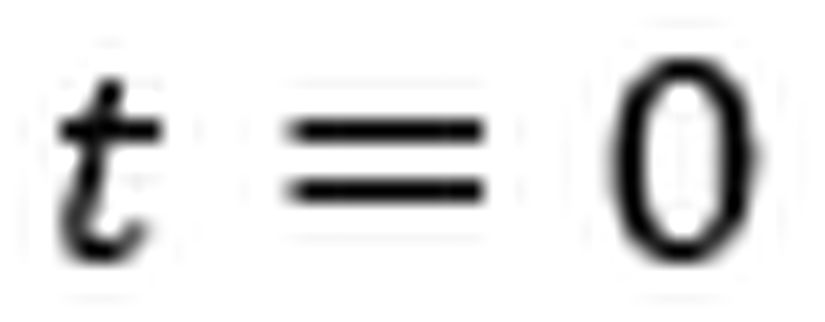
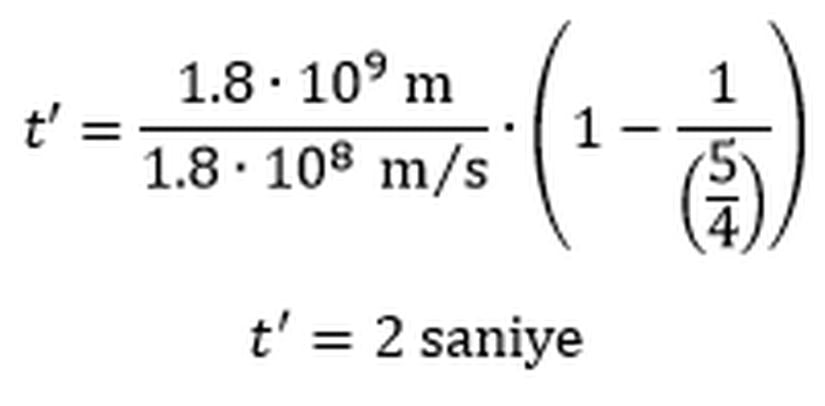
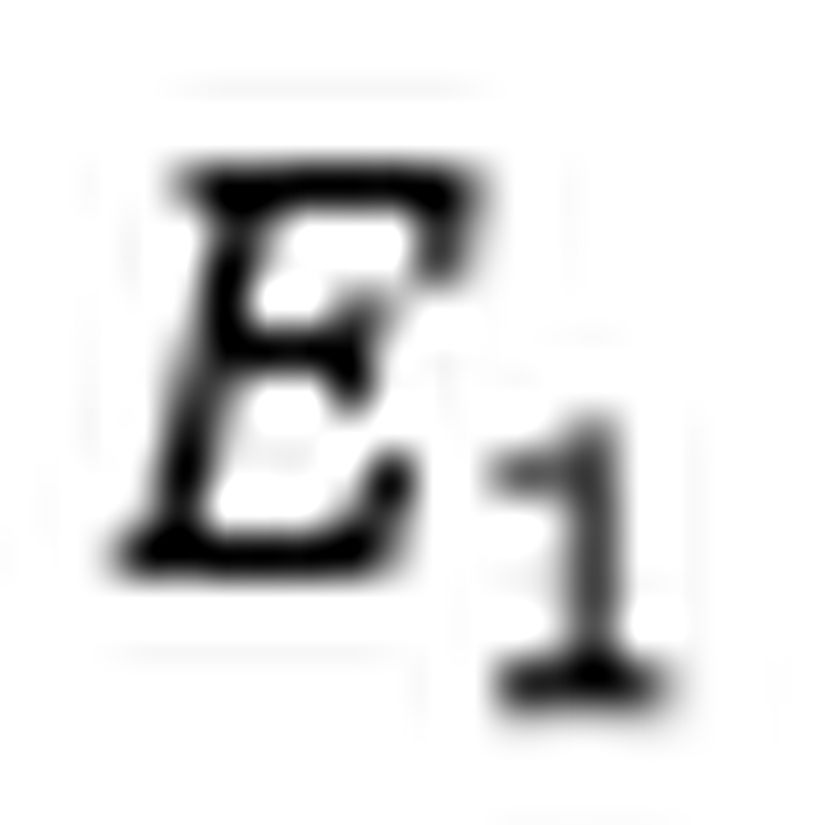
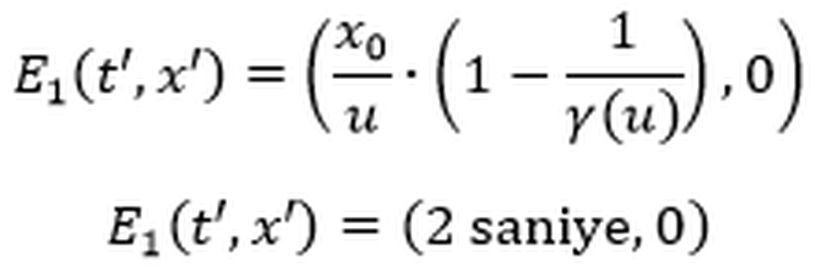
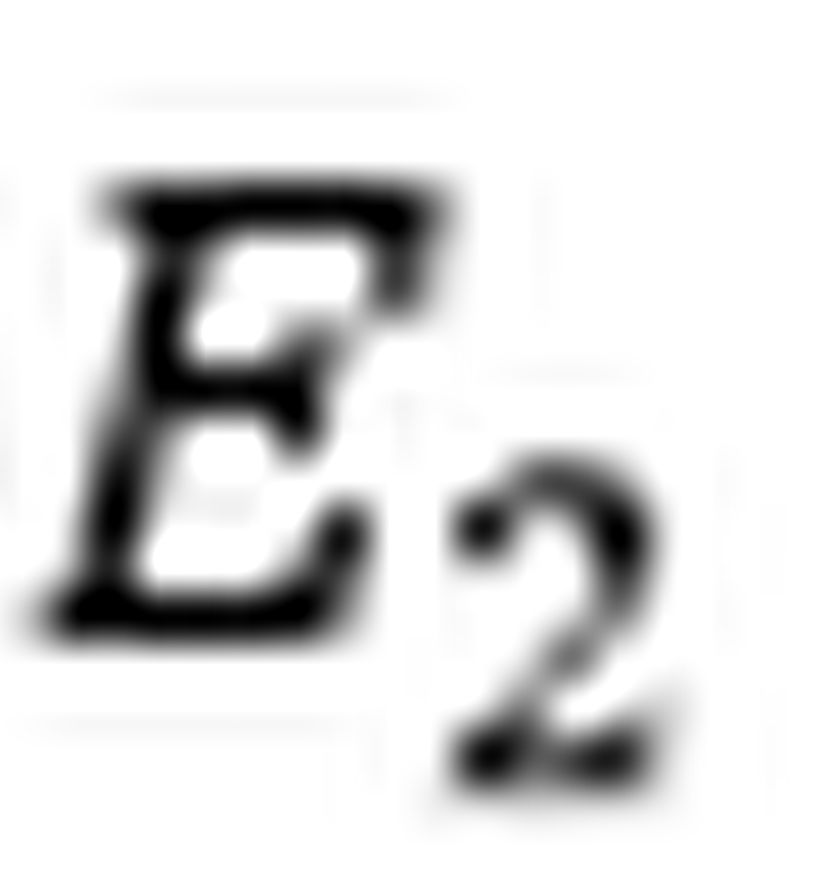

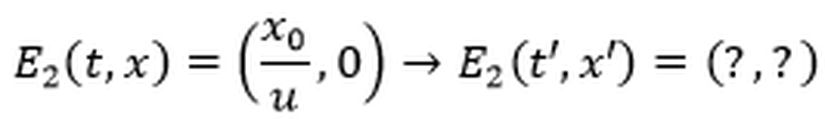
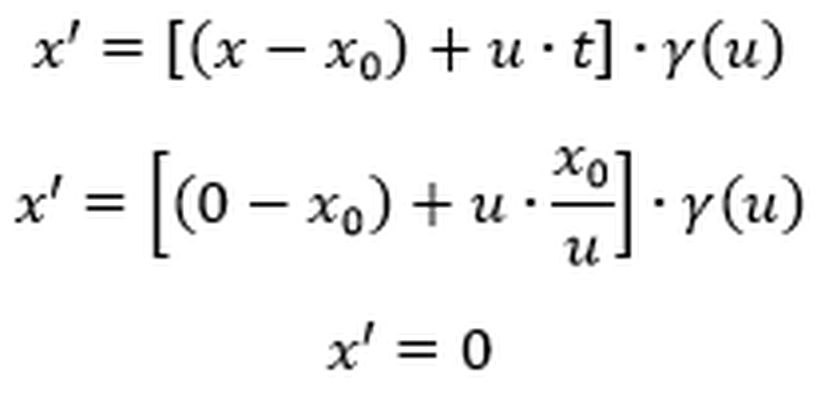
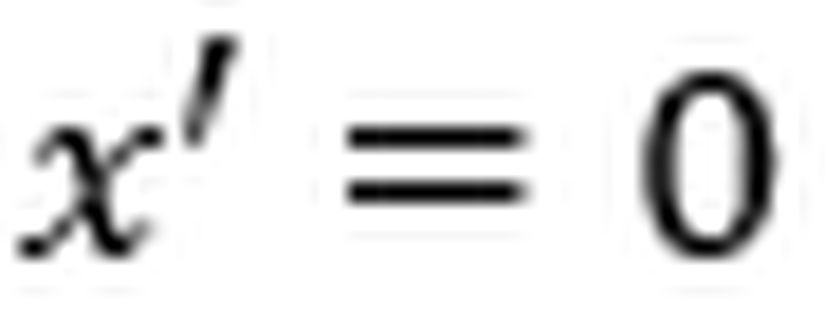
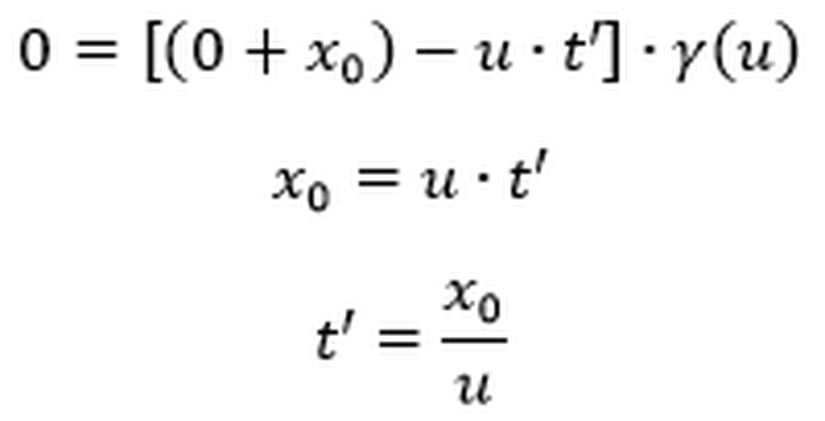
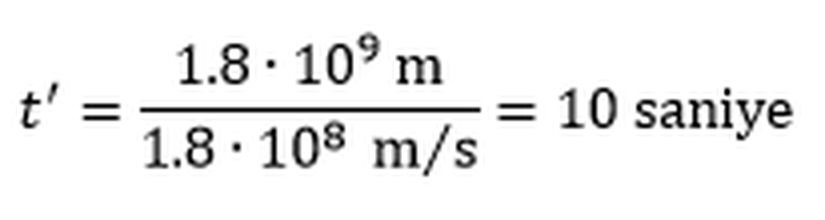
O halde
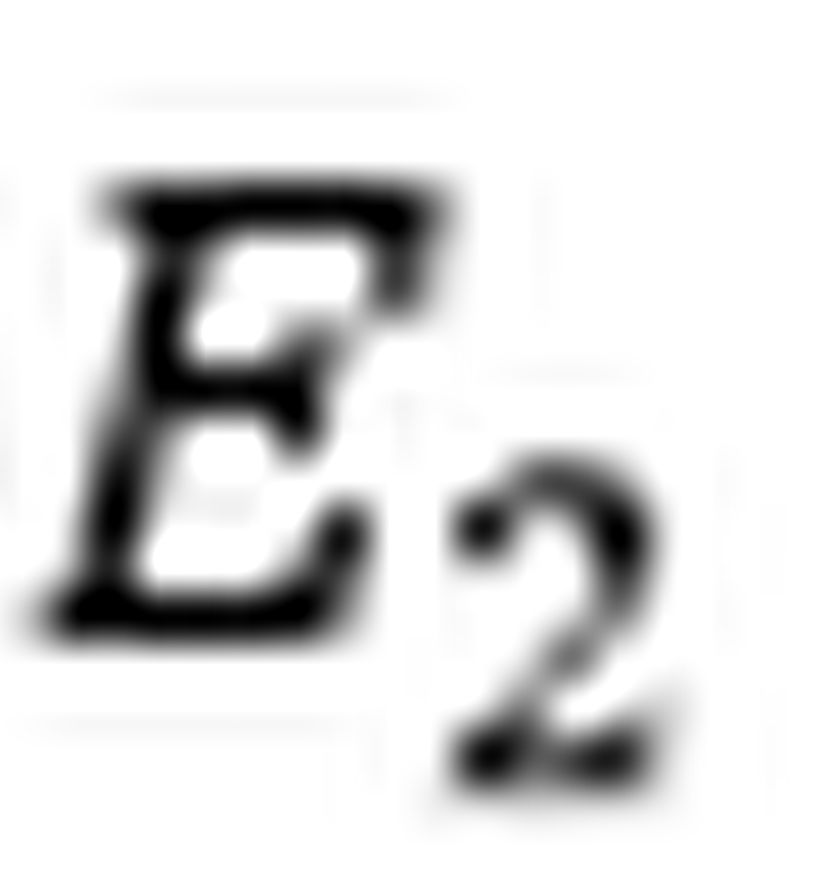
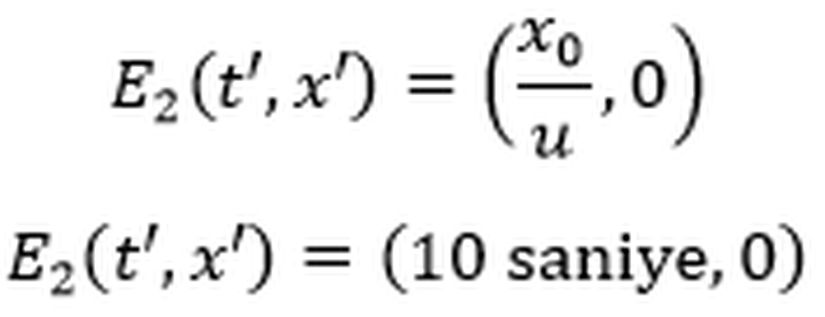
Ek olarak her iki olay arasında geçen sürenin Ali’nin ve Ayşe’nin gözlem çerçevelerinde ölçülen değerleri arasında nasıl bir ilişki olduğunu hesaplayalım.
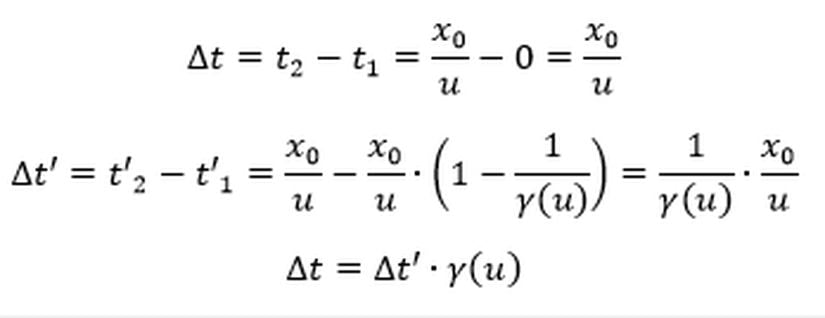
Bu yazı da eşzamanlılığın göreliliğinin ihmal edilmesi durumunda ne gibi paradokslar ortaya çıktığını anlatmaya çalıştık ve gördük ki eşzamanlılığı göz önünde bulundurduğumuz zaman ortada hiçbir paradoks yoktur.
Ege Özmeral
Referanslar ve İleri Okuma
1. Green B.,WorldScienceU, <http://www.worldscienceu.com/courses/university/special-relativity>
2. Serway R.A., & Jewett J. W., Physics for Scientists and Engineers, Vol. 1 - Modern Physics
3. Landau L.D. &LiftshitzE.M., The Classical Theory of Fields, Third Revised English Edition.
Kapak görseli: <https://nootropicdesign.com/defusableclock/gallery.html>
Evrim Ağacı'nda tek bir hedefimiz var: Bilimsel gerçekleri en doğru, tarafsız ve kolay anlaşılır şekilde Türkiye'ye ulaştırmak. Ancak tahmin edebileceğiniz gibi Türkiye'de bilim anlatmak hiç kolay bir iş değil; hele ki bir yandan ekonomik bir hayatta kalma mücadelesi verirken...
O nedenle sizin desteklerinize ihtiyacımız var. Eğer yazılarımızı okuyanların %1'i bize bütçesinin elverdiği kadar destek olmayı seçseydi, bir daha tek bir reklam göstermeden Evrim Ağacı'nın bütün bilim iletişimi faaliyetlerini sürdürebilirdik. Bir düşünün: sadece %1'i...
O %1'i inşa etmemize yardım eder misiniz? Evrim Ağacı Premium üyesi olarak, ekibimizin size ve Türkiye'ye bilimi daha etkili ve profesyonel bir şekilde ulaştırmamızı mümkün kılmış olacaksınız. Ayrıca size olan minnetimizin bir ifadesi olarak, çok sayıda ayrıcalığa erişim sağlayacaksınız.
Makalelerimizin bilimsel gerçekleri doğru bir şekilde yansıtması için en üst düzey çabayı gösteriyoruz. Gözünüze doğru gelmeyen bir şey varsa, mümkünse güvenilir kaynaklarınızla birlikte bize ulaşın!
Bu makalemizle ilgili merak ettiğin bir şey mi var? Buraya tıklayarak sorabilirsin.
Soru & Cevap Platformuna Git- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
Evrim Ağacı'na her ay sadece 1 kahve ısmarlayarak destek olmak ister misiniz?
Şu iki siteden birini kullanarak şimdi destek olabilirsiniz:
kreosus.com/evrimagaci | patreon.com/evrimagaci
Çıktı Bilgisi: Bu sayfa, Evrim Ağacı yazdırma aracı kullanılarak 02/06/2025 07:29:45 tarihinde oluşturulmuştur. Evrim Ağacı'ndaki içeriklerin tamamı, birden fazla editör tarafından, durmaksızın elden geçirilmekte, güncellenmekte ve geliştirilmektedir. Dolayısıyla bu çıktının alındığı tarihten sonra yapılan güncellemeleri görmek ve bu içeriğin en güncel halini okumak için lütfen şu adrese gidiniz: https://evrimagaci.org/s/12658
İçerik Kullanım İzinleri: Evrim Ağacı'ndaki yazılı içerikler orijinallerine hiçbir şekilde dokunulmadığı müddetçe izin alınmaksızın paylaşılabilir, kopyalanabilir, yapıştırılabilir, çoğaltılabilir, basılabilir, dağıtılabilir, yayılabilir, alıntılanabilir. Ancak bu içeriklerin hiçbiri izin alınmaksızın değiştirilemez ve değiştirilmiş halleri Evrim Ağacı'na aitmiş gibi sunulamaz. Benzer şekilde, içeriklerin hiçbiri, söz konusu içeriğin açıkça belirtilmiş yazarlarından ve Evrim Ağacı'ndan başkasına aitmiş gibi sunulamaz. Bu sayfa izin alınmaksızın düzenlenemez, Evrim Ağacı logosu, yazar/editör bilgileri ve içeriğin diğer kısımları izin alınmaksızın değiştirilemez veya kaldırılamaz.




