Kuantum Mekaniği: de Broglie Dalga Boyu

Tıpkı ışık gibi, maddenin de bir dalga özelliği olduğunu düşünerek yola çıkan de Broglie, kütleye sahip maddesel parçacıklar için bir dalga boyu tanımına ulaşmıştır. Günümüzde bu ifadeye kaşifine ithafen de Broglie dalga boyu diyoruz. Tecrübe ettiğimiz, gündelik olaylardaki nesnelerin kütlesi göz önüne alındığında bu dalga boyunun, aşırı küçük olduğunu buluruz. Bu nedenle bizim boyutumuzdaki nesnelerin dalga özelliğinden ziyade, bizlere göre aşırı düşük kütleli parçacıkların dalga özelliğinden bahsederiz.
20. yüzyılın başlarında, etrafımızı çevreleyen evreni anlama yolunda ciddi adımlar atıldı. Bu adımların en önemlilerinden ikisi fotoelektrik olayve compton saçılmasıdır. Bu iki çalışma bizlere, ışığın enerji ve momentuma sahip fotonlar (parçacıklar) halinde yayıldığını söyler. Ancak, ışık ile yapılan girişim ve kırınım deneyleri de bizlere ışığın dalga özelliği gösterdiğini reddedilemez şekilde gösterir. Işığın söz konusu ikili doğası, günlük yaşamdaki deneyimlerimizle çeliştiği için kabullenmesi epey güç bir konudur. Aklınıza “sadece ışık mı ikili doğaya sahiptir?”sorusu gelmiş olabilir. Endişelenmeyin, bu soruyu soran ilk kişi siz değilsiniz.
1923 yılında, genç ve heyecanlı fizikçi Louis de Broglie, doktora tezinde: "Fotonlar hem dalga hem de parçacık özelliklerine sahipler. Belki maddenin her türlü şekli bu iki özelliğe sahiptir" öngörüsünde bulundu.

de Broglie Dalga Boyu

de Broglie’ye göre, elektronların kararlı hareketlerinde karşımıza tamsayı değerler çıkmasının, tamsayı değerler ile açıklanan girişim ve titreşim ile bir bağlantısı vardı. Öngördüğü bu bağlantıdan yola çıkan de Broglie, elektronların yalnızca parçacıklar olarak düşünülemeyeceğini, aynı zamanda dalga doğasına da sahip olmaları gerektiğini düşündü.
Fotonun dalga boyu ile momentumu arasındaki bağıntıdan (P=h/λ) yola çıkan de Broglie, ışık için geçerli bu formülün, kütleye sahip (maddesel) parçacıklar için de geçerli olacağını öngördü. de Broglie’ye göre kütlesi m, hızı v olan bir parçacığın de Broglie dalga boyu aşağıdaki gibidir:

Bağıntıdan da görüldüğü üzere, büyük kütleli cisimlerin dalga boyu, önemsenmeyecek kadar küçük olmaktadır.  Bu yüzden bizim gibi büyük cisimlerin, dalga özelliğinden pek bahsetmeyiz.
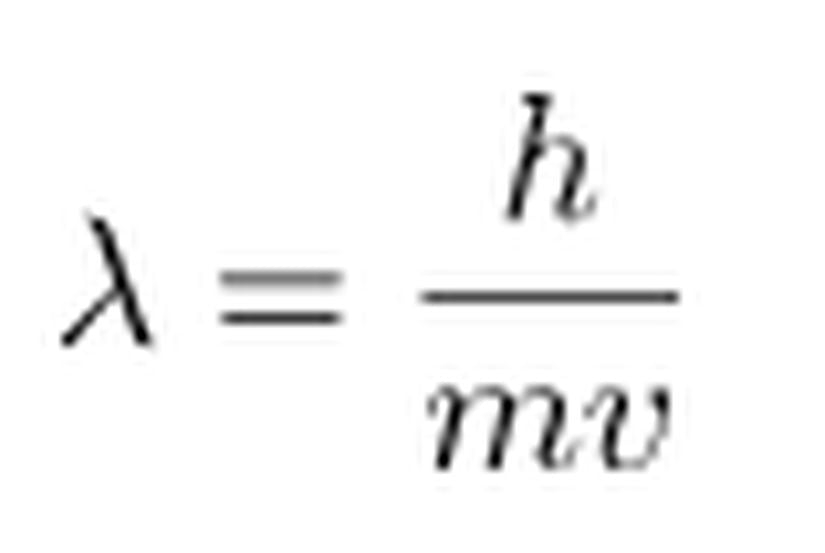
Madde dalgaları ismini verdiği bu dalgaların, 1927 yılında C. Davisson ve L. Germer tarafından deneysel olarak doğrulanmasından yalnızca iki yıl sonra, de Broglie’nin doktora tezi Nobel'e layık görüldü.
Madde dalgaları konuşulduğunda, aklımıza "madde dalgalarında zamana bağlı şekilde periyodik olarak değişen, yani dalga formunu oluşturan şey nedir?" sorusu gelebilir.
Bu sorunun yanıtı, diğer yazılarımızda açıklayacağımız üzere, atomun kuantum modelinin gelişimine götürecek kadar ciddi bir öneme sahip.
Su dalgalarında, periyodik olarak değişen şey su yüksekliğidir. Ses dalgalarında ise bu, basınçtır. Işıkta ise, periyodik olarak değişen şey, elektrik ve manyetik alandır.
Madde dalgaları söz konusu olduğunda ise, bu periyodik değişimleri yapan nicelik "dalga fonksiyonu" olarak isimlendirilir. Dalga fonksiyonunun çözümleri ise, bir parçacığın; herhangi bir zamanda, belirli bir konumdaki bulunma olasılığıyla ilişkilidir.
Eğer bu konu ile ilk kez karşılaşıyorsanız, yazdıklarımız ilk okuyuşta biraz karışık gelebilir. Ancak, belki ufak bir kopya, bu konuyu daha iyi anlamanızı sağlayabilir. Yukarıdaki "dalga fonksiyonu" diye bahsettiğimiz şey, ψ sembolü ile gösterilmektedir. Şimdi biraz daha tanıdık gelmiş olmalı. Kuantum dünyasına giriş yapmak sizleri de heyecanlandırdı mı? Çünkü biz çok heyecanlıyız.
Yukarıda, dalga fonksiyonu hakkında konuşurken, dalga fonksiyonunun çözümünün, parçacığın bulunma olasılığıyla "ilişkili" olduğunu söylemiştik. "İlişkili" kelimesini kullanmamızın bir sebebi vardı.
Dalga fonksiyonunun kendisi, yani ψ, kendi başına gözlemlenebilir bir büyüklük değildir. Bildiğimiz gibi, olasılık dediğimiz şey, 0 ile 1 arasındadır. Ancak, dalga fonksiyonunun büyüklüğü, pozitif ya da negatif bir değer olabilir. Bu sebeple, ψ değil, ψ² bizlere parçacığın, o noktadaki bulunma olasılığını verir. Bu büyüklüğe, olasılık yoğunluğu (probability density) denir.
Bu noktada, karşımıza çıkabilecek diğer bir kafa karışıklığı ise, bir olayın gerçekleşme olasılığı ile olayın kendisi arasındaki farktır. Yani, bir elektron uzayın belirli bir noktasında ya vardır ya da yoktur. Elektronun %60'ının orada olması gibi bir şey söz konusu değildir. Elektronun, uzayın o noktasında bulunma ihtimali %60'tır.
W.L. Bragg, bu konuda şunu söylemektedir:

"Gelecekteki her şey, dalgadır. Geçmişteki her şey ise parçacık."

---

Hazırlayan: Ege Can Karanfil
Referanslar
1. Serway ve Beichner, Fizik 3 (Modern Fizik) 5. Baskı, Syf. 1311
2. Namık K. Tunalı ve Saim Özkar, Anorganik Kimya, Syf. 10
3. Beiser, Concepts of Modern Physics, 6th edition
4. <https://chem.libretexts.org/Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/Supplemental_Modules_(Physical_and_Theoretical_Chemistry)/Quantum_Mechanics/02._Fundamental_Concepts_of_Quantum_Mechanics/Deriving_the_de_Broglie_Wavelength>