Eşkenar Üçgen Nedir? Formülleri ve Özellikleri

Üç kenarı bulunan ve tüm kenar uzunlukları ile açıları birbirine eşit olan geometrik şekle eşkenar üçgen denir. Tüm üçgenlerin iç açıları toplamı 180 derecedir (Öklidyen uzayda). Buradan hareketle diyebiliriz ki eşkenar üçgenin her iç açısı 60°'ye eşittir.

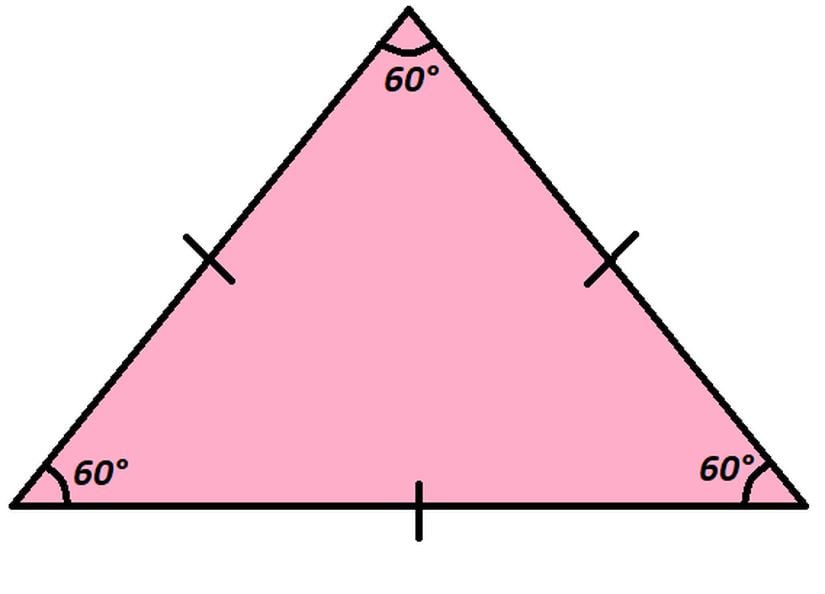
Eşkenar dörtgen ile kare ve dikdörtgen ile kare arasında gördüğümüz birinin diğerini kapsamasıyla ilgili bağlantı, üçgenler arasında da mevcuttur. Her ne kadar bu yazımızın konusu olmasa da birazdan bahsedeceğimiz bağlantıyı anlamak adına kısaca ikizkenar üçgenin ne olduğundan bahsetmekte yarar var. İki kenarı ve ilgili iki iç açısı birbirine eşit olan üçgenlere ikizkenar üçgen denir. Bu tanımdan yola çıkarak her eşkenar üçgenin aynı zamanda bir ikizkenar üçgen olduğunu söyleyebiliriz. Tabii tersi geçerli değildir, yani her ikizkenar üçgen bir eşkenar üçgen değildir.

Eşkenar Üçgen Özellikleri ve Formülleri

1. Eşkenar Üçgende Köşegenler

Köşegen, bir çokgende ardışık olmayan iki köşeyi birleştiren doğru parçasıdır. Herhangi bir üçgene baktığımızda ise ardışık olmayan, yani bir kenar ile birbirine bağlanmamış olan, iki köşe bulunmadığını görürüz. Yani eşkenar üçgen de dahil olmak üzere hiçbir üçgenin köşegeni yoktur.

2. Eşkenar Üçgende Açıortay, Kenartortay ve Simetri

Bir açıyı, ölçüleri birbirine eşit olan iki açısal bölgeye ayıran doğru parçasına açıortay denir. Benzer şekilde bir çokgenin bir kenarını iki eş parçaya ayıran doğru parçasına ise kenarortay denir. Eşkenar üçgenin herhangi bir köşesinden karşı kenara çizeceğiniz açıortay, aynı zamanda o kenarın kenarortayı olacaktır.

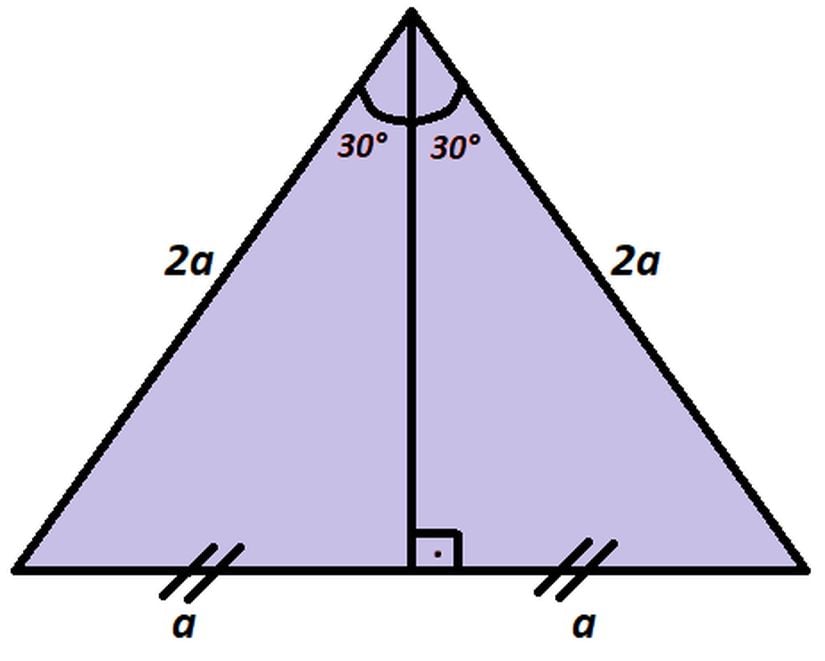
Şekilde de görüldüğü üzere herhangi bir köşeden çizdiğimiz açıortay, karşı kenarı iki eş parçaya ayırmakla kalmaz, aynı zamanda bu kenara dik iner.

Bu özel üçgenin tüm açıortaylarını çizdiğimizde bunların hepsi tek bir noktada kesişir ve birbirlerini 1:2 oranında bölerler. Aşağıdaki şekli inceleyerek ne demek istediğimizi daha net anlayabilirsiniz.

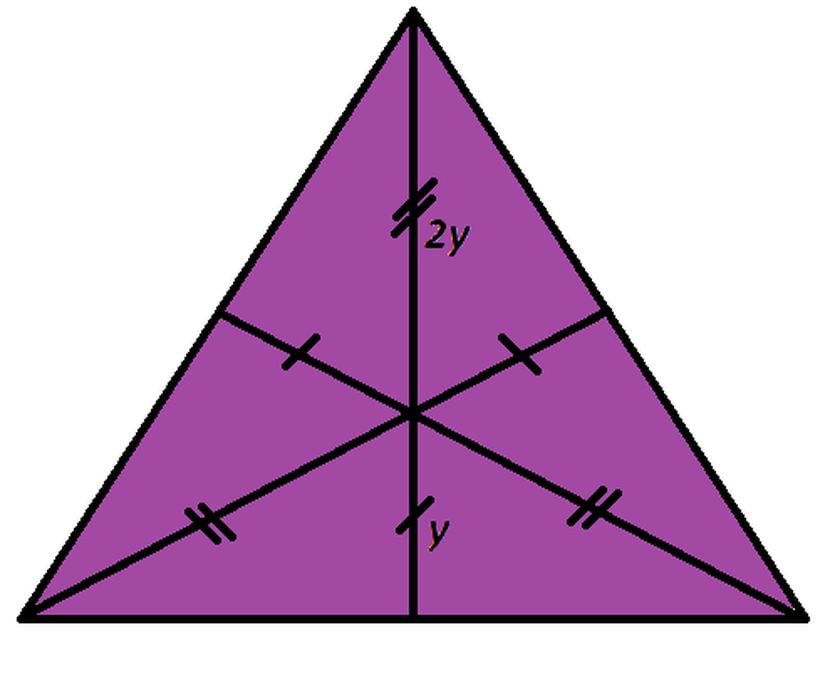
Eşkenar üçgende açıortayın özellikleri bu kadarla da sınırlı değil. Kendisi aynı zamanda üçgenimizin simetri eksenidir. Yani elinizde eşkenar üçgen şeklinde bir kâğıt varsa ve bunu açıortay doğrusu boyunca katlarsanız her iki tarafın tam birbirinin üstüne geldiğini göreceksiniz. Bu durum üç açıortay doğrusu için de geçerlidir. Burada bu özel üçgenin 60°'lerde oluşturduğu simetrilere dikkat etmek isteyebilirsiniz.

3. Çevrel Çember ve İç Teğet Çember

Eşkenar dörtgen yazımızda bahsettiğimiz gibi, çevrel çember, bir çokgeni çevreleyen ve tüm köşelerini üzerinde bulunduran çembere denir. İç teğet çember ise bir çokgenin içinde bulunan ve çokgenin tüm kenarlarına teğet olan çemberin adıdır. Tüm üçgenlerin, düzgün çokgenlerin (tüm kenarları ve açıları birbirine eşit olan) ve bazı düzgün olmayan çokgenlerin çevrel çemberi ve iç teğet çemberi vardır.

Üçgenimizin açıortaylarının tek bir noktada kesiştiğinden bahsetmiştik. Bu nokta aynı zamanda üçgenimizin hem çevrel hem de iç teğet çemberlerinin merkezi olur.

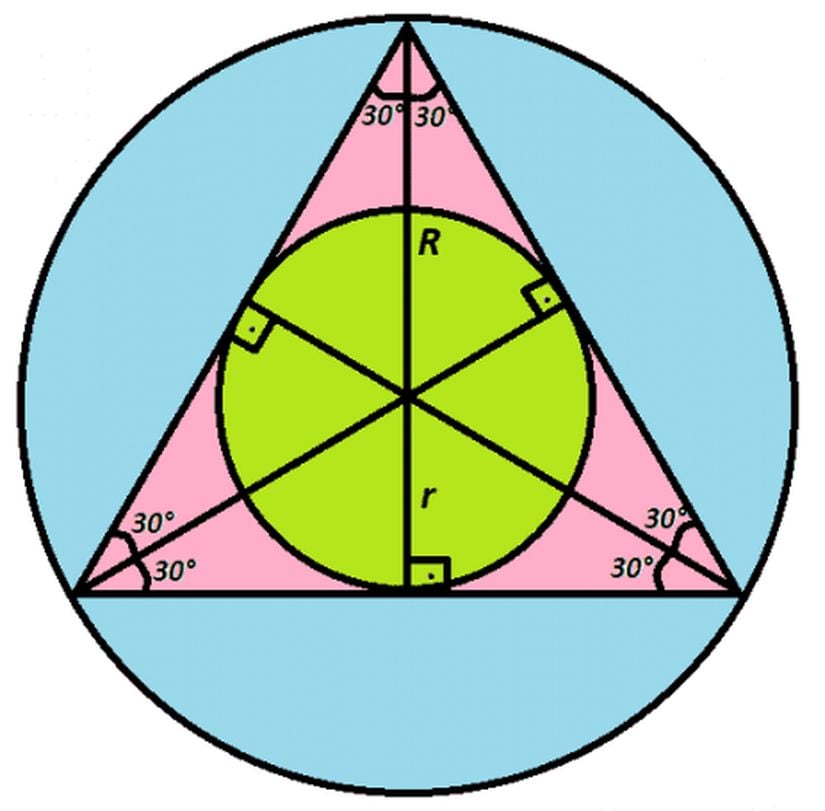
Eğer ki üçgenin bir kenar uzunluğu biliniyorsa bu çemberlerin yarıçaplarını ve alanlarını bulmak mümkündür. Tabii bu noktada işin içine biraz da trigonometri karışıyor.

Eğer iç teğet çemberin yarıçap uzunluğunar, çevrel çemberin yarıçap uzunluğuna R ve üçgenin bir kenar uzunluğuna a dersek üç farklı şekilde yarıçapları elde edebiliriz:

Evrim Ağacı'ndan Mesaj

Neden Desteğe İhtiyacımız Var?

Aslında maddi destek istememizin nedeni çok basit: Çünkü Evrim Ağacı, bizim tek mesleğimiz, tek gelir kaynağımız. Birçoklarının aksine bizler, sosyal medyada gördüğünüz makale ve videolarımızı hobi olarak, mesleğimizden arta kalan zamanlarda yapmıyoruz. Dolayısıyla bu işi sürdürebilmek için gelir elde etmemiz gerekiyor.

Bunda elbette ki hiçbir sakınca yok; kimin, ne şartlar altında yayın yapmayı seçtiği büyük oranda bir tercih meselesi. Ne var ki biz, eğer ana mesleklerimizi icra edecek olursak (yani kendi mesleğimiz doğrultusunda bir iş sahibi olursak) Evrim Ağacı'na zaman ayıramayacağımızı, ayakta tutamayacağımızı biliyoruz. Çünkü az sonra detaylarını vereceğimiz üzere, Evrim Ağacı sosyal medyada denk geldiğiniz makale ve videolardan çok daha büyük, kapsamlı ve aşırı zaman alan bir bilim platformu projesi. Bu nedenle bizler, meslek olarak Evrim Ağacı'nı seçtik.

Eğer hem Evrim Ağacı'ndan hayatımızı idame ettirecek, mesleklerimizi bırakmayı en azından kısmen meşrulaştıracak ve mantıklı kılacak kadar bir gelir kaynağı elde edemezsek, mecburen Evrim Ağacı'nı bırakıp, kendi mesleklerimize döneceğiz. Ama bunu istemiyoruz ve bu nedenle didiniyoruz.

Destek Ol

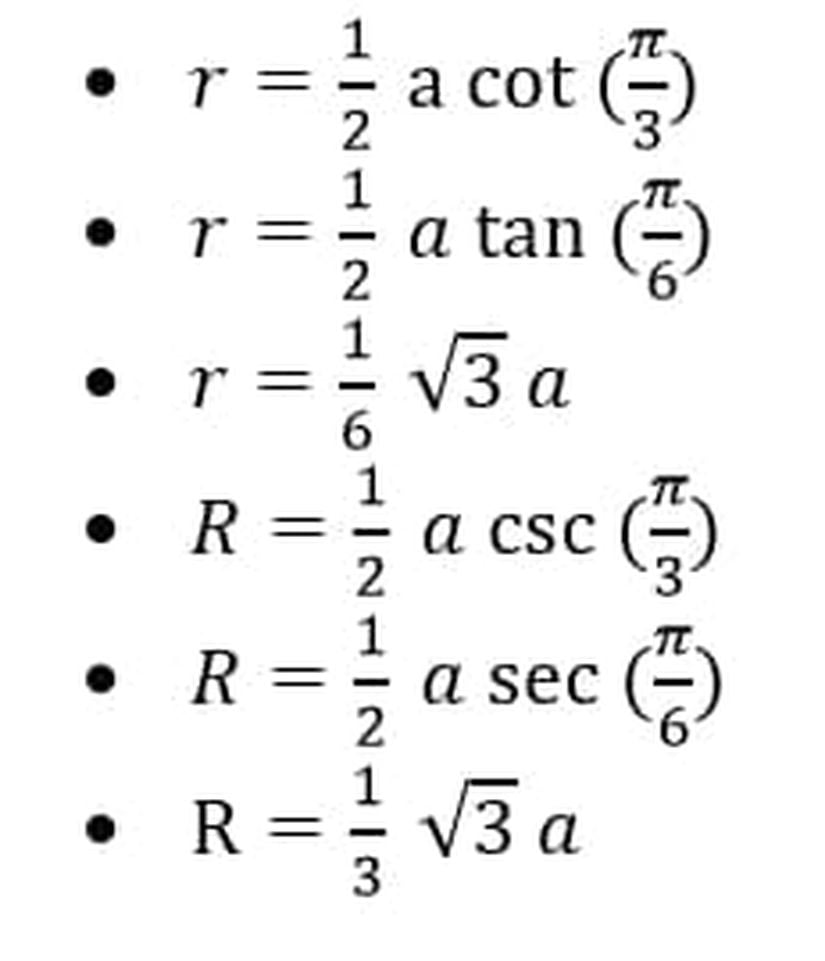
Bu durumda iç teğet çemberin alanı ve çevrel çemberin alanı şu formüller ile bulunur:

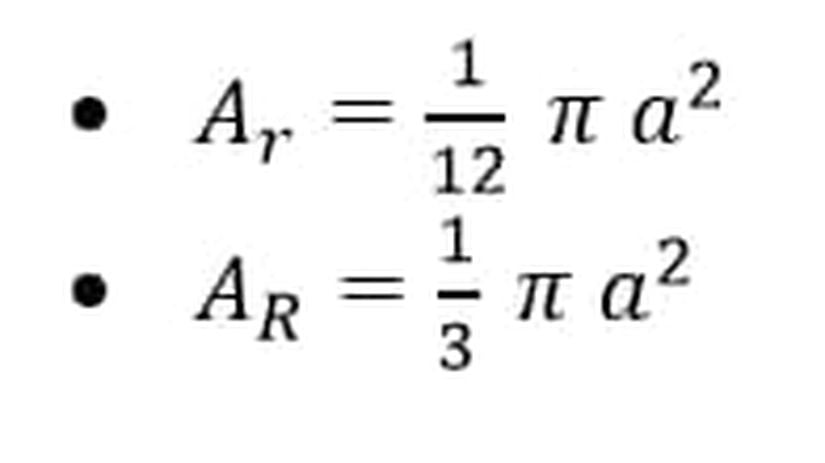
4. Eşkenar Üçgende Alan

Bir kenarı bilinen eşkenar üçgenin alanını bulmak için bir de yüksekliğe ihtiyacımız vardır. İhtiyacımız olan yükseklik, kenar uzunluğu kullanılarak elde edilebilir. Pisagor teoreminden veya basit trigonometri bilgimizden faydalanarak, bir kenar uzunluğu a olan eşkenar üçgende yükseklik (h) aşağıdaki şekilde bulunur.

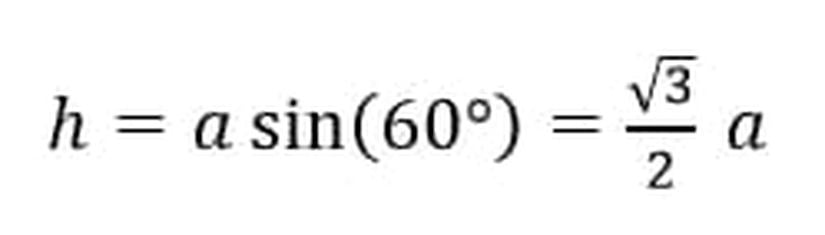
Daha sonra alan(A), taban çarpı yüksekliğin yarısı olarak aşağıdaki şekilde bulunur. Burada yükseklik (h)'yi yerine yazdığımızda oldukça sıradan bir alan formülüyle karşılarız.

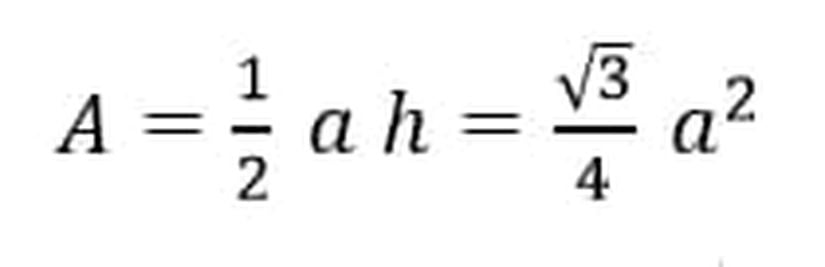
Eşkenar üçgende alan formülü bu şekilde tanımlanır.

5. Eşkenar Üçgenin Çevresi

Keza eşkenar üçgende çevrenin hesabı oldukça basittir. Hemen göreceğiniz üzere, bir kenara a dersek, toplam çevre 3a olacaktır. Çünkü bu üçgende tüm kenarlar birbirine eşittir.

Hiç kuşkusuz bu özel üçgenle ilgili birçok şey söylenebilir, özellikle simetrilerinden ötürü tanımlanabilecek bir sürü özelliği bulunur. Lakin bunlar bu yazının amacı dışında kaldığından, bunlara henüz değinmiyoruz. Yine de tüm bu bilgiler ışığında, sizin buna biraz kafa yormanızı ve farklı neler görebileceğinizi sorgulamanız önemli!

Hazırlayan:Arya Elçi
Editör:Ögetay Kayalı

Referanslar:
1.Wolfram Mathworld, "Equilateral Triangle", < https://mathworld.wolfram.com/EquilateralTriangle.html >