Compton Saçılması

20. yüzyıl, nükleer teknolojilerin keşfi sebebiyle, atomaltı dünyanın anlaşılması açısından pek çok dönüm noktasına sahiptir. Compton saçılması adı verilen ve Arthur H. Compton ekibi tarafından nükleer teknolojiler kullanılarak yapılan deneylerdeki davranış, yalnızca ışığın kuantum modelini kullanarak açıklanabilecekti.
Klasik elektrodinamiğe göre, elektromanyetik dalga (ışık) elektronun üzerine düştüğünde, elektron salınım yapmaya başlar. Bu sayede elektron, gelen ışığı her yönde yayar. Elektronun salımının frekansı, gelen ışığın frekansıyla aynıdır. Bu sebeple klasik olarak, saçılan ışığın dalga boyu, elektrona düşen ışığın dalga boyuna eşittir.
Lakin, 1923 yılında Arthur Compton ve ekibi tarafından, X-ışınları ile yapılan deneylerde, elektronun üzerine düşen ışığın dalga boyu ile saçılan ışığın dalga boyu arasında fark olduğu gözlemlenir.
Işığın kuantum modeline göre ışık, parçacık gibi davranır.
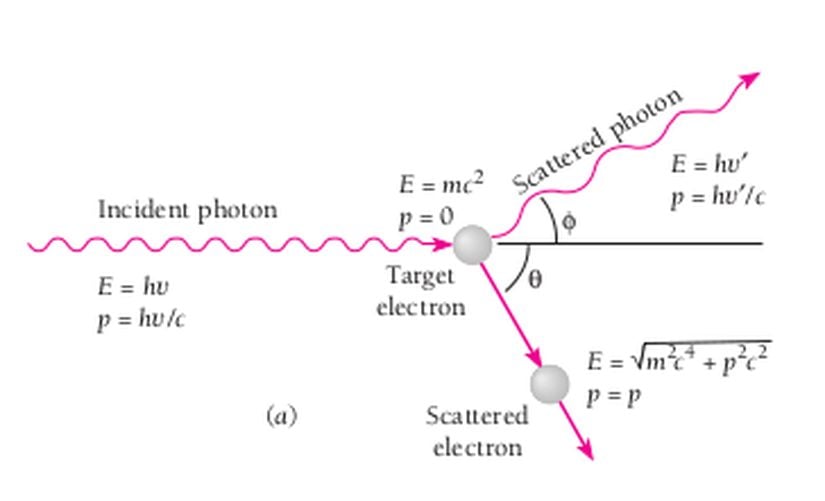
Arthur H. Compton saçılan X ışınlarının dalga boyunun değişme sebebini, 1905 yılında Albert Einstein'ın öne sürdüğü ışığın kuantumlu modelini kullanarak açıkladı. Compton Saçılması olarak adlandırılan bu olay, ışığın parçacık özelliğinin en önemli ispatlarından birisidir.  Compton saçılmasını açıklamak için elektron ve fotonlar, iki bilardo topunun çarpışmasına benzer şekilde modellenmektedir.

https://rasyonalist.org/yazi/klasik-dalga-teorisinin-cokusu-fotoelektrik-olay/
https://rasyonalist.org/yazi/nukleer-fizik-gama-%ce%b3-isimasi/

Compton Saçılması Deneyi

Compton saçılması deneyinde, X ışını tüpünde oluşturulan X ışınları, karbon bloğa gönderilir. Bu bloktan saçılan ışınlar, Bragg spektrometresiyle gözlemlenir ve bu sayede, saçılan fotonların dalga boyu tespit edilir.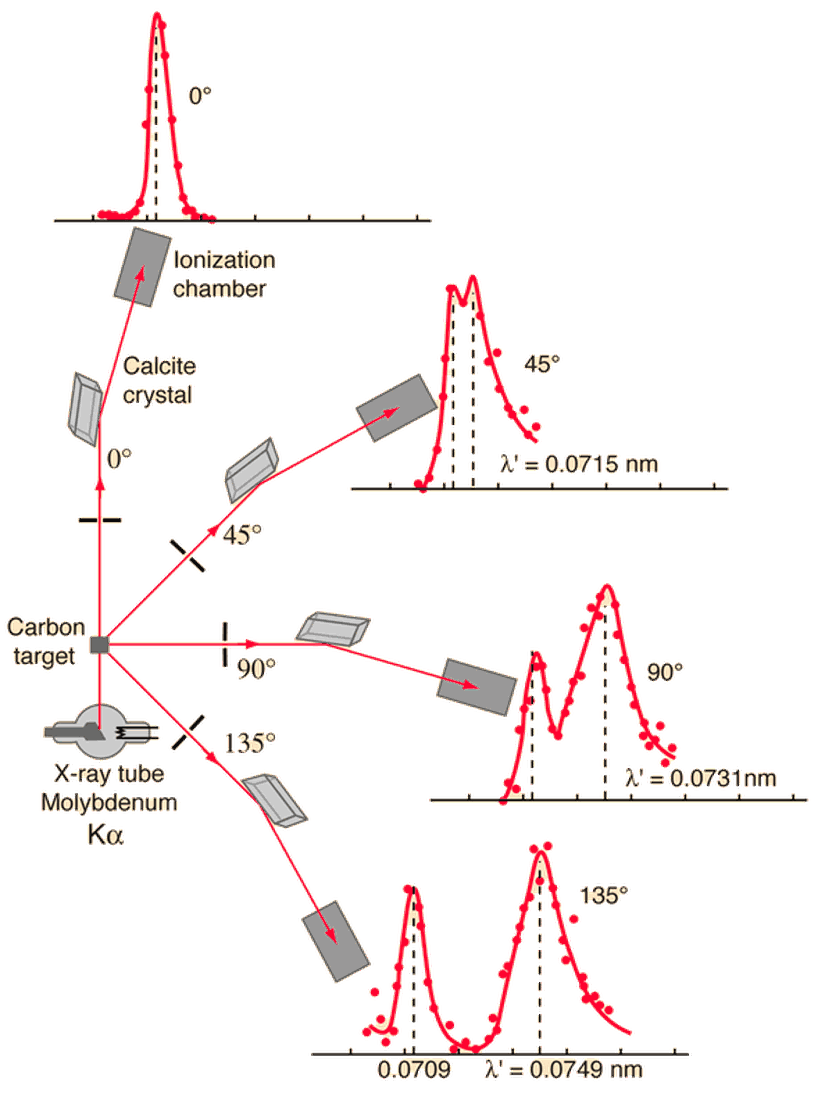

İç bölgeler daha sıkı şekilde birbirine bağlı olduğu için, foton nispeten serbest haldeki elektronlardan değil, atoma sımsıkı bağlı elektronlardan saçılır. Bu saçılma sonucunda, atoma sıkıca bağlı olan elektron hareket etmeyeceğinden, fotonun dalga boyunda ciddi bir değişim gözükmez. Yüzeye yakın bölgelerden yansıyan x ışınlarının dalga boyu ise, compton saçılması adı verilen etki sebebiyle değişir (konsept, yazımızın sonunda çok daha iyi anlaşılacaktır).
Bu değişimin büyüklüğü, saçılan fotonların düzlemle yaptığı açı ile değişmektedir. Değişim, yukarıdaki figürde görülebilir. Artan açı, dalga boyundaki değişimi de arttırmaktadır.

Compton Saçılması

Saçılan ışığın dalga boyunun, elektrona çarpan ışığın dalga boyundan farklı oldğunu görmek bir şey, bunun neden olduğunu anlamak başka bir şey. Deneyin ayrıntılarını konuşurken, bu değişimi nasıl gözlemleyeceğimizi gördük. Şimdi de, neden bu değişimi gördüğümüzü, yani Compton saçılmasının ardındaki fiziği tartışalım.
Bildiğimiz tek bir şey varsa, o da enerjinin korunumu ve momentumun korunumu yasalarıdır. Bu iki yasayı kullanarak, durumu anlamaya çalışalım. Fotoelektrik olayıaçıklayan Einstein, foton enerjisini hν olarak ifade etmişti. Buradaki ν, fotonun frekansına karşılık gelmektedir. Öyleyse, frekansı (dalga boyu) değişen fotonun enerjisi bir yerlere gitmeli. Kuşkusuz bizim sistemimizde bu enerjinin gittiği yer elektronun kinetik enerjisi. Yani:

Enerji momentum eşitliğini hatırlayacak olursak:

Foton, kütlesiz bir parçacık olarak tanımlandığı için, fotonun enerjisi E, pc'ye eşit olacaktır. Foton enerjisi E'yi, hν olarak tanımlamıştık. Yerine yazacak olursak:

halini alır. Bu sayede, frekansı ν olan fotonun momentum ifadesini yazmış oluruz. Hatırlarsanız, bildiğimiz iki şey olduğundan, birinin enerji korunumu, diğerinin de momentumun korunumu olduğundan bahsetmiştik.
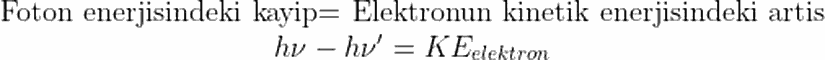
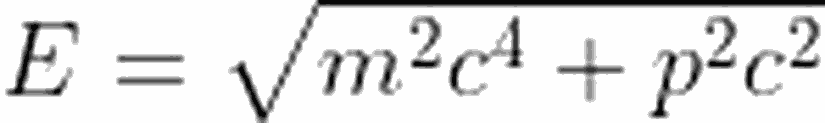
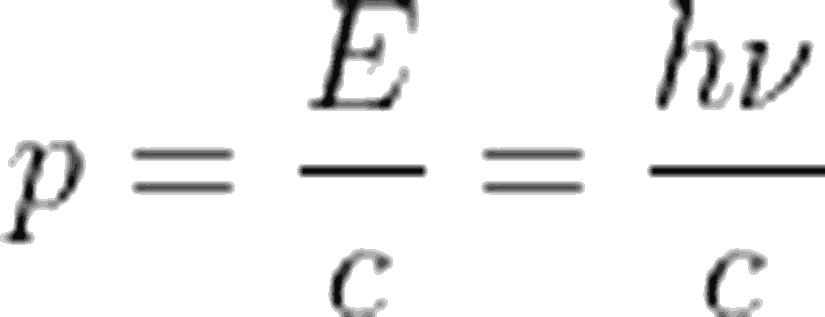
Artık fotonun momentumunu bize veren ifadeyi bildiğimize göre, yukarıdaki sistem için momentumun korunumu eşitliğini de yazabiliriz. Vektörel olarak ilk momentumun son momentuma eşit olması gerektiğini biliyoruz. Yatay ve düşey eksen için momentum ifadelerini yazacak olursak, yatay eksen için:

halini alır. Düşey eksen için ise, eğer yukarı yönü pozitif alırsak:

haline gelir. Burada Φ açısı saçılan fotonun, Θ ise saçılan elektronun yatay eksenle yaptığı açı anlamına gelir. Elimizdeki tüm bilgi, yukarıda yazdıklarımızdan ibaret. Şimdi, fırça darbeleriyle önündeki tuvalde harikalar yaratan bir sanatçı misali, bu bilgileri kullanarak, saçılan fotonların frekansındaki (dalga boyundaki) değişimi bize veren bir ifade bulma zamanı.
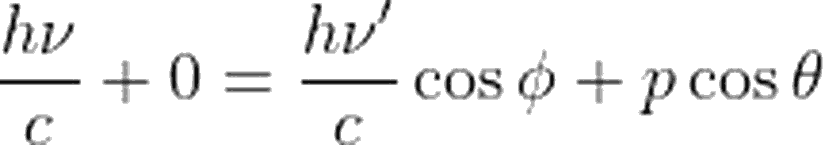
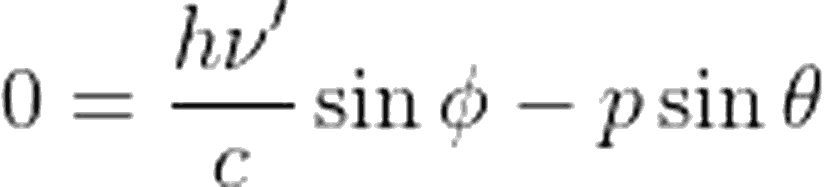
Öncelikle, daha rahat düzenleyebilmek adına yukarıdaki iki denklemi c ile çarpalım.

Şimdi, sinüs ve cosinüs ifadelerini azaltmak adına, her iki denklemin karesini alalım ve ardından bu iki denklemi taraf tarafa toplayalım.

Denklemde, enerji momentum eşitliğinden aşina olduğumuz p²c²'yi görmekteyiz. Öyleyse, enerji momentum ifadesini kullanarak, p²c² için bir ifade türetmeye çalışalım. Parçacığın toplam enerjisini aşağıdaki gibi ifade edebiliriz:

Yazımızın başında, enerjinin korunumu için yazdığımız denklemi, p²c²eşitliğinde yerine yazarsak:

haline gelir. Şimdi, bulduğumuz bu ifadeyi, ilk elde ettiğimiz p²c² denklemiyle eşitleyelim. Böylece,

haline gelir. Aslında, Compton saçılmasında, elektrona çarpan ve saçılan foton arasındaki frekans farkını veren ifadeyi bulmuş olduk. Lakin, daha anlaşılır bir hal alması adına, ifadeyi dalga boyu cinsinden yazalım. Bunun için ifadeyi 2h²c²'ye bölelim. Bu sayede ifade:

c=ν.λ ifadesini hatırlayalım. Buna göre, λ=ν/c olacağından, denklemimiz aşağıdaki hale gelir:

İfademiz gitgide tanıdık hale geliyor. Son olarak, ufak bir düzenleme daha yapalım. Denklemimiz:

haline gelecektir. Bu sayede, 1923 yılında Arthur H. Compton tarafından keşfedilen bu konseptin, yani Compton saçılmasının yine Arthur H. Compton tarafından yapılan matematiksel açıklamasını ispat etmiş olduk.
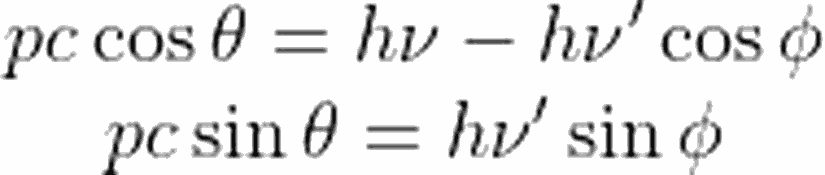
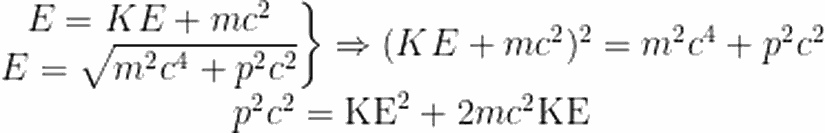
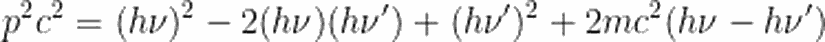
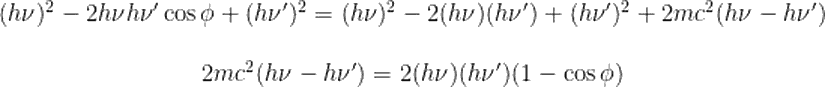
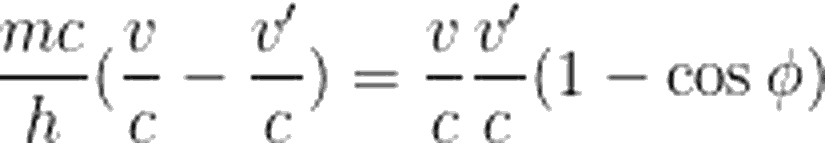
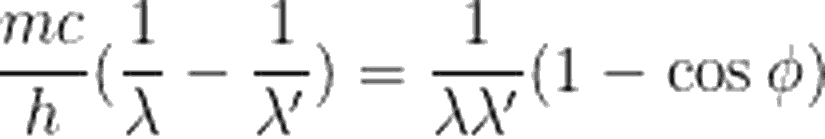
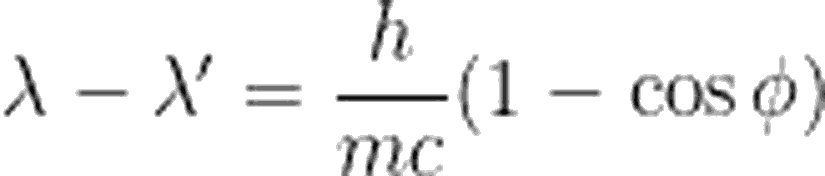
Yazımızın başında, atoma daha sıkı şekilde bağlı olan elektronlardan yapılan saçılma sonrasında, fotonun dalga boyunda değişim görülmeyeceğini söylemiştik. Bu durumda, saçılma atomdan yapılıyormuş gibi düşünülebilir. Böyle bir durumda da, fotonun çarptığı parçacığın kütlesi çok daha büyük olacağından, denklemimizdeki "m" çok daha büyük bir değer alır. Bu da, denklemin sağ tarafının sıfıra yakın olmasına sebep olur. Yani parçacığa düşen ve saçılan fotonun dalga boyundaki değişim, sıfır olmuş olur.
Nükleer fizik yazı dizimizde ele aldığımız gama radyasonunun, madde ile etkileşim yöntemlerinden birisi olan Compton saçılması, son derece kritik bir etkileşim çeşididir. Gama radyasyonunun biyolojik etkileri hesaplanırken, bu yüksek enerjili fotonların, dokuyla olan etkileşiminde, Compton saçılması da göz önünde bulundurulur.
Hazırlayan: Ege Can Karanfil
Referanslar
1. Arthur Beiser, Concepts of Modern Physics, McGraw Hill, 2003, Chapter 2.7
2. Prof. Dr. Bilge Demirköz, Modern Physics ders notları
3. Hyperphysics, "Compton Scattering Data"
<http://hyperphysics.phy-astr.gsu.edu/hbase/quantum/compdat.html#c1>
4. Richard Fitzpatrick, "Thomson Scattering"
<https://farside.ph.utexas.edu/teaching/jk1/lectures/node107.html>
5. Geoffrey V. Bicknell, "Compton Scattering"
Kapak Görseli
http://wanda.fiu.edu/boeglinw/courses/Modern_lab_manual3/Compton_Scattering.html