A groundbreaking computational method has been unveiled to tackle the intricate realms of quantum physics, particularly in the study of quantum many-body systems. This new quantum Monte Carlo (QMC) scheme significantly enhances the extraction of the reduced density matrix (RDM) and the entanglement spectrum (ES), key concepts in understanding quantum entanglement and measurement. The proposed method addresses longstanding computational limitations, previously hindering researchers from exploring the complete entangling regions in larger quantum systems.
The research, published on March 24, 2025, in Nature Communications, showcases how the newly developed scheme allows for the extraction of the RDM with unprecedented precision, enabling scientists to gain deeper insights into the intricate properties of quantum systems. Specific features of the work include simulating a one-dimensional (1D) Heisenberg ladder and a two-dimensional (2D) Heisenberg model, which reveal long-range interactions and the fundamental nature of entanglement in these systems.
"This method can obtain ρA for much larger system sizes," noted the researchers, emphasizing its capabilities beyond the confines of earlier approaches. Traditional numerical methods, like exact diagonalization (ED) and density matrix renormalization group (DMRG), often faced challenges due to computational complexities that grow rapidly as system sizes increase. In contrast, the QMC approach integrates ED while leveraging powerful sampling techniques, streamlining the process.
The RDM is instrumental as it encapsulates almost all physical quantities related to the reduced degrees of freedom within a quantum system, essentially acting as a generator for critical information about the system's state. Furthermore, the enhanced method provides an efficient way to restore the entanglement Hamiltonian (EH) from the RDM data, showcasing its versatility. "An efficient way to restore the entanglement Hamiltonian in operator form from the RDM data," emphasizes the unique advantage it offers to physicists analyzing complex systems.
The significance of the ES, defined as the logarithmic eigenvalues of the RDM, comes into play here, representing a more fundamental characteristic to quantify intrinsic information within many-body systems. Quantum entanglement allows researchers to gain direct insights into topological properties, critical for understanding transitions and states within quantum mechanics. Nevertheless, prior studies have often been limited to smaller, one-dimensional or quasi-one-dimensional systems, because of computational constraints.
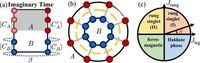
This new QMC framework establishes a practical computational approach making it feasible to simulate larger systems accurately, as evidenced by the simulations performed on a two-leg Heisenberg ladder model, where specific parameters were fine-tuned for optimal results. The study reflects on a scenario with Jleg = 1 and Jrung = 1.732, allowing researchers to study the system’s properties extensively across various configurations.
Alongside the practical benefits of these advancements in computational methods, the research results indicate the velocity is almost unchanged with size L, converging to approximately 2.41. This observation is pivotal, since it was inconsistent with results obtained in other studies, further validating the reliability of the QMC method adopted.
Moreover, the 2D aspects of the study highlight the entanglement characteristics from various geometrical configurations. A PBC (periodic boundary condition) 20 × 20 square lattice AFM (antiferromagnetic) Heisenberg model was calculated to unveil further distinct properties, showcasing how different configurations within the same underlying system could produce varying insights into symmetry-breaking characteristics.
As researchers delve into the realm of quantum many-body physics with newfound accessibility, the implications of the presented work are far-reaching. Established methods of measuring crucial variables, such as von Neumann entropy and entanglement negativity, become more manageable. The results also pave the way for additional observable analytics that could utilize this practical scheme to expand quantum mechanics’ frontiers further.
The intricate dance of particles in quantum systems can now be examined with less computational burden, empowering scientists to unlock longstanding mysteries in quantum entanglement. The promising applications of this new approach not only promise to enhance quantum simulations but also open avenues for future research aimed at deepening our understanding of complex quantum interactions.