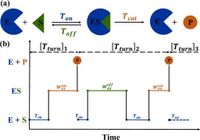
In a groundbreaking development in enzymatic research, scientists have introduced high-order Michaelis-Menten equations that enhance our understanding of enzyme kinetics at a single-molecule level. Traditional Michaelis-Menten dynamics have long been crucial in explaining enzyme behavior, outlining how enzymes catalyze reactions by binding to substrates to form enzyme-substrate complexes. Yet, this framework has limitations, particularly in fully capturing the lifetimes of these enzyme-substrate complexes, the rates of binding, and the probabilities of successful product formation.
Recent research has forged ahead by deriving a new set of equations which extend the Michaelis-Menten framework. These high-order equations reveal linear relationships between vital kinetic parameters—such as the lifetime of the enzyme-substrate complexes and the rates at which substrates bind and unbind from enzymes—and the reciprocal of substrate concentration. In essence, this work offers a more nuanced perspective into enzyme function, equipping researchers with the tools necessary to glean critical insights that were previously elusive.
"The traditional Michaelis-Menten equation provided a sound basis for understanding enzyme kinetics, yet it only allowed us to extract limited information," noted the authors of the article. They stressed the importance of the new equations, stating they can derive kinetic parameters that shed light on how enzymes behave under varying conditions.
The rigorous testing of these equations demonstrated their resilience. The scientists found that even with only several thousand turnover events per substrate concentration, the equations produced accurate results, indicating great potential for broad applications in biochemistry and molecular biology.
Enzymes, as nature's biocatalysts, play essential roles across biological processes, facilitating biochemical reactions necessary for life. Their dynamic functions typically follow the well-studied Michaelis-Menten kinetics, which describe how enzymes interact with substrates to produce products. However, much about their underlying processes remained hitherto inaccessible—until now.
This newly derived methodology allows scientists to obtain insights into the intimate workings of enzyme activity, such as the average lifetime of the enzyme-substrate complex, crucial for understanding reaction rates and mechanisms. The authors demonstrated how these high-order Michaelis-Menten equations might help acquire estimates of these kinetic parameters systematically.
What sets this study apart is the framework's versatility in tackling both Markovian and non-Markovian enzymes. The former relates to processes that do not rely on memory—the sequential states in enzyme kinetics don't influence future states. Conversely, non-Markovian models incorporate such memory effects, reflecting a broader range of enzyme behaviors that could influence catalytic efficiency.
Crucially, the researchers revealed that even non-Markovian enzymes could still be analyzed using the newly formulated equations, with reasonable estimates obtainable when certain conditions are satisfied. This broad applicability marks a significant advancement in enzymatic research, potentially influencing the development of biocatalysts in industry and therapeutic practices.
This research also opens the door for future studies to delve deeper into the peculiarities of enzyme kinetics, investigating how various factors, such as conformational dynamics within enzyme structures or external environmental conditions, modulate catalytic performance.
In conclusion, the introduction of high-order Michaelis-Menten equations constitutes a significant leap forward in understanding enzymatic processes, illustrating their power in providing insights into the hidden parameters of enzyme kinetics. The robust nature of these equations presents a valuable tool for researchers seeking to explore the complexities of enzyme behavior, while potentially paving the way for novel applications in biotechnology and medicine.