Dengue fever, a viral disease endemic to tropical and subtropical regions, has emerged as a significant public health concern, particularly in Nepal. Recent research introduces a mathematical model that offers critical insights into the disease's transmission dynamics, revealing substantial implications for both public health policy and economic impact.
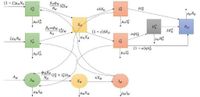
Developed by a team of researchers, the model categorizes humans into several classes: high-risk and low-risk susceptibles, exposed, asymptomatic and symptomatic infections, hospitalized patients, and those recovered, alongside a three-class mosquito population. This differentiation allows for a nuanced analysis of disease spread and prevention strategies. By fitting this model to historical data from 2004 to 2022, the researchers assessed how various parameters influence the basic reproduction number, denoted as 0R0, which estimates how many people an infected individual is expected to transmit the virus to in a susceptible population.
Utilizing analytical methods and numerical simulations, the study demonstrated both the local and global stability of equilibrium points within the model. "The model has been validated to ensure the positivity and boundedness of solutions," wrote the authors of the article, highlighting the robust nature of their calculations. Their statistical analysis showcased that the model explained approximately 86.78% of the variance in the dengue infection data across Nepal, indicating a strong correlation between predicted and actual cases.
In light of the increasing trend in dengue cases, which began with the first recorded incidences in the country in 2004, this modeling effort has timely potential. The study underscores the significance of controlling the populations of Aedes mosquitoes—transmitters of the dengue virus—through targeted health interventions and effective management strategies aimed at reducing breeding sites. These analyses align with the ongoing effort to integrate innovative biological control methods, particularly through the implementation of Wolbachia-infected mosquitoes to diminish virus transmission rates.
The research not only explored the mathematical underpinnings of dengue dynamics but also accounted for the disease's economic and psychological toll on affected populations in Nepal. "This study aims to fill this gap by developing a mathematical framework that simulates the dynamics of dengue transmission in Nepal but also considers the economic and social burden of the disease," emphasized the authors. As the analysis revealed, the financial burden is acute; families often face significant expenses related to hospitalization and treatment, forcing them into moral dilemmas that may affect their long-term stability.
Moreover, increased hospitalization rates can lead to productivity losses, further impacting Nepal's economy. In 2022, the lost productivity due to dengue was estimated at approximately 547,800 person-hours, a stark illustration of the extensive implications of the outbreak. With predictions extending to 2030, it is anticipated that the number of hospitalizations will begin to decrease if effective control measures, including potential vaccination strategies, are adopted. Conversely, the population of infected mosquitoes may rise due to favorable environmental conditions, such as prolonged monsoon seasons promoting mosquito breeding.
Ultimately, the model serves as a vital tool for health policymakers, assisting in devising evidence-based strategies that reflect the complexities of dengue transmission. As noted by the authors, "We have analytically and graphically demonstrated that both the Dengue-free and endemic equilibrium points are locally and globally stable." This confirmation of stability highlights the feasibility of targeted interventions that could lead to sustained reductions in dengue morbidity and mortality across the region.
In summary, the mathematical modeling of dengue fever in Nepal encapsulates a significant advancement in understanding and controlling infectious diseases. It not only offers critical evaluations of current epidemiological trends but also emphasizes the need for integrated approaches to tackle the broader socio-economic burdens posed by the disease. Continued research efforts are necessary to adapt and refine these models to cope with changing environmental and social dynamics in the ongoing fight against dengue fever.