Kuantum Mekaniği: Lineer Bağımlılık ve Lineer Bağımsızlık

Kuantum mekaniğinin dilinde lineer cebirin öneminden bahsetmiştik. Lineer cebirde de bizim için en önemli konulardan biri lineer bağımlılık ve lineer bağımsızlıktır. Bazen "iki vektör birbirinden lineer bağımsız olmalı" deriz, peki bununla neyi ima etmek isteriz?

Diyelim ki iki tane birbirine paralel olmayan |V> ve |W> vektörlerimiz olsun. Bunları toplarsak |V> + |W> şeklinde başka bir vektör elde ederiz. Peki bunları a ve b gibi herhangi iki reel skalerle çarparsak ne olur? Bunu önce matematiksel olarak ifade edelim.

a|V>+b|W>

Buna |V> ve |W> vektörlerinin lineer kombinasyonları diyeceğiz.Burada a ve b herhangi bir reel sayı, dolayısıyla burada tüm reel sayıları kapsayan çeşitli kombinasyonlarda |V> ve |W> vektörlerini yeniden ölçeklendiriyor (negatifse tersi yönde çevirerek ölçeklendiriyor) ve toplayarak başka bir vektör elde ediyoruz. Sonuç olarak elimizde sadece bu iki vektörün ve bu iki keyfi skalerin tanımladığı bir vektörler kümesi oluyor. Buna germe (span) adını veriyoruz. Fazla tanımlama yaptık ve biraz soyut kaldı, biliyorum. O nedenle anlattığımızı görselleştirmeye çalışalım.

Sezgisel olarak da anlayacağımız üzere bu iki vektörün ilgili lineer kombinasyonuyla aynı düzlemde yer alan diğer vektörlerden herhangi birini tanımlayabiliriz. Dolayısıyla 2 boyutlu uzayda yer alan çoğu vektörün germesi, 2 boyutlu bir uzaydaki tüm vektörlerdir. Burada çoğu dediğimize dikkat edin, çünkü başta bir kabul yapmıştık. Bu iki vektör birbirine paralel olmayacaktı. Peki paralel olursa ne olur?

İki vektörün birbirine paralel olması durumunda, bunların lineer kombinasyonları yine aynı doğrultu üzerinde yer alır. Bu sefer 2 boyutlu bir uzay söz konusu değildir, daha kaba bir tabirle, tüm kombinasyonları düşünecek olsak dahi, 2 boyutlu düzlemi oluşturacak bir vektör kümesi ortaya çıkmaz. Çok daha kaba bir tabirle bu iki vektör aynı doğru üzerinde yer alırlar. Dolayısıyla bunların lineer kombinasyonları sadece bu doğru parçasının uzunluğunu değiştirir.

Üç Boyutta Vektörlerin Germesi (Spanı)

Az önce sadece iki vektörden bahsettik, peki bu iki vektör üç boyutta yer alırsa bunların germesi ne olur? Sezgisel olarak bunun yine bir düzlem olacağını ve bu düzlemin hangi düzlem olacağının da bu vektörlere bağlı olacağını hemen söyleyebilirsiniz. Peki üç boyutlu bir uzayda üç vektörün germesi hakkında ne söyleyebiliriz? Bunun cevabını sezgisel olarak bulmak için iki tanesiyle bir düzlem oluşturduğunuzu ve üçüncünün kombinasyonuyla da bu düzlemi uzayda (ileri-geri) tarattığınızı düşünebilirsiniz. Yani aslında bu, uzayın tamamını ifade edecektir. Fakat bu üç vektörden birisi diğerine paralelse, yine bir düzlemle kısıtlanırız. Hepsinin birbirine paralel olması durumunda da yine tek boyuta düşer.

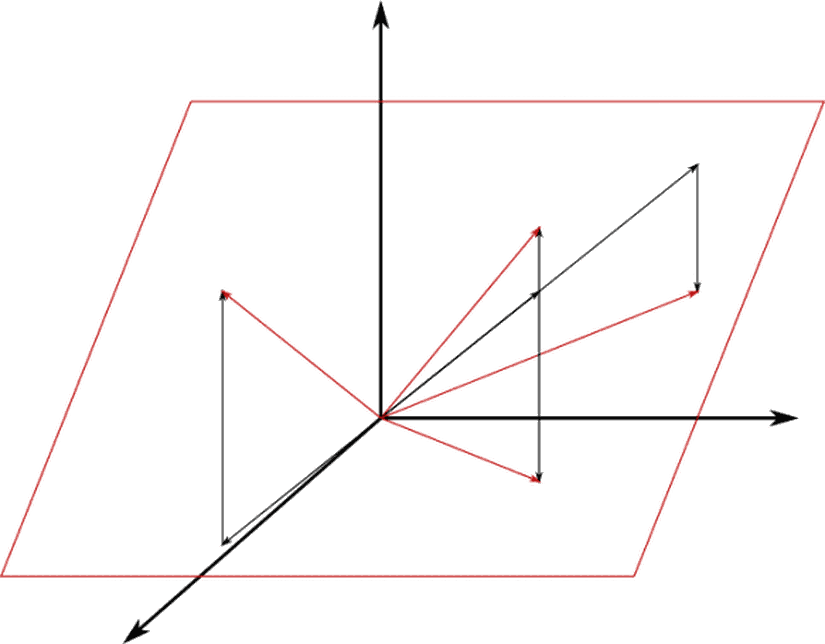
Şimdi tüm bunlar ne anlama geliyor? Tahmin edeceğiniz üzere aslında birbirine paralel olan veya olmayan vektörlerin, lineer kombinasyonlarının verdiği sonuçların farkını inceliyor ve bir tanımlama yapmaya çalışıyoruz. Örneğin eğer üçüncü vektörün eklenmesi germeye bir katkı yapıp, onu bir düzlemden üç boyutlu uzayın tamamına taşımıyorsa, bu üçüncü vektörün, diğer iki vektörden birine lineer bağımlı olduğunu söyleriz.

Dolayısıyla özet olarak, eğer her bir vektör, germenin boyutunu artırıyorsa, bu vektörler lineer bağımsızdır. Fakat eğer bir vektör toplama eklendiği halde germenin boyutunu artırmıyorsa, bu vektör diğerlerinden birinin lineer kombinasyonu olarak ifade edilebilir, dolayısıyla lineer bağımlıdır.

Bir başka deyişle lineer bağımlı olan vektör, zaten diğer vektörlerin oluşturduğu germenin içerisinde yer alır.

Bir vektör uzayının bazı (basis) ise, uzayın tamamını geren lineer bağımsız vektörler kümesidir. Bunun sıkça üzerinde şapka olan i ve j ile gösterildiğini görebilirsiniz, fakat elbette ki herhangi bir harfle ifade edilebilir. Üzerinde şapka olması durumunda genel olarak onların birer baz vektör olduğunu ifade ederiz.

Lineer Bağımlılık ve Lineer Bağımsızlık Bağımlılık

Yukarıdaki sezgisel açıklamalarımızı sindirdiğimize göre, lineer bağımsızlığı aşağıdaki şekilde tanımlayabiliriz.

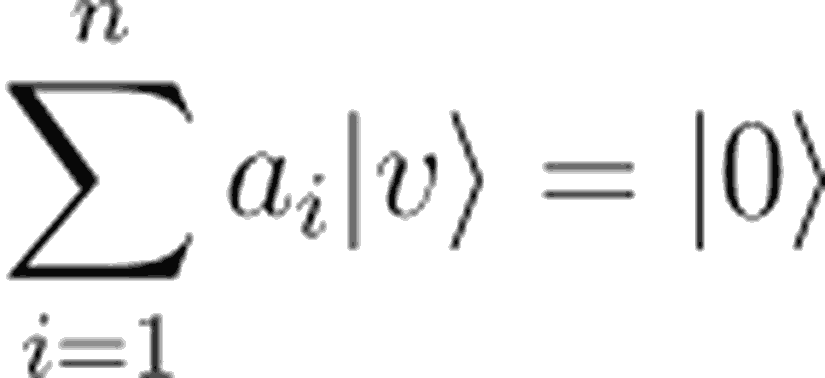
Eğer yukarıdaki ilişkide a_i=0 bayağı çözümü tek çözümse, bu vektörler lineer bağımsızdır. Eğer değilse, lineer bağımlıdır. Buradaki |v> vektörünü n adet lineer bağımsız baz vektörleri cinsinden yazabiliriz.

Burada |i> vektörleri baz oluşturur. Aslında şu anda matematiksel olarak gösterdiklerimiz, bir daha önce anlattıklarımızın sadece denklemlere dökülmüş halidir. Burada v_i bir skalerdir ve baz vektörü olan i ile çarptığımızda (n-boyutlu uzayda her i için n kere) bize toplamda v vektörünü verir. v_i skalerlerine ilgili vektörün bileşenleri de denir.

Örneğin x, y ve z baz vektörleri için bu üç boyutta yer alan bir vektörü 3x+2y+5z şeklinde ifade edebiliriz. Burada v₁=3, v₂=2 ve v₃=5'tir. |1>=x, |2>=y ve |3>=z şeklinde ifade ettiğimize dikkat edin. Eğer bunlar kafa karıştırıcı geliyorsa toplamları açarak yazıp görmeniz yardımcı olacaktır. Kabaca yukarıdaki toplamı 3 boyutlu uzay için şu şekilde açabiliriz: |v>=v₁|1>+v₂|2>+v₃|3>. Burada v₁, v₂ ve v₃ ilgili baz vektörlerinin bileşenleridir.

Aşağıdaki dört boyutlu örneği ele alalım.

Bu dört vektör birbirinden lineer bağımsızdır. Ya da bir başka deyişle birini diğerlerinin lineer kombinasyonları şeklinde ifade etmek mümkün değildir. Bu sayede herhangi bir 2x2 matrisi bu dört vektörün lineer kombinasyonu şeklinde ifade edebiliriz.

Daha basit bir ifadeyle a, b, c ve d'yi keyfi olarak değiştirerek tüm 2x2 matrisleri yazmak mümkündür. Eğer burada a, b, c ve d reel sayılardan oluşuyorsa buna reel dört boyutlu bir uzay, eğer kompleks sayılardan oluşuyorsa kompleks dört boyutlu uzay deriz.

Bu noktada şuna dikkat çekmek gerek, bu matrislerin sıfırlardan ve birlerden oluşması bir zorunluluk değil. Örneğin birinci matristeki bir sayısı yerine 2 olsaydı da bunlar yine lineer bağımsız olacaktı. Çünkü diğer matrislerin birinci satır, birinci sütunda sadece sıfır var. Dolayısıyla bunu diğerleri cinsinden, bazı skalerlerle çarparak elde etmek mümkün değil.

Tüm bu kavramları daha iyi anlamak için muhakkak referanstaki 3Blue1Brown animasyonlu anlatımına göz atmanızı öneriyoruz. Listedeki bütün lineer cebir videoları, bu konuları anlamanıza çok yardımcı olacaktır.

Agora Bilim Pazarı

W. Benjamin - G. Scholem Mektuplaşmalar 1932-1940

İki büyük savaşın damga vurduğu karanlıkta, tüm güçlüklere karşın bağlarını sürdürme çabalarından vazgeçmeyen Almanyalı iki Yahudi entelektüelin 1932’den 1940’a dek süren mektuplaşmaları, hem döneme hem de yazarlarına ilişkin çok önemli bilgiler sunuyor. 20. yüzyılın en önemli edebiyat ve sanat eleştirmeni olarak ölümünden sonra üne kavuşan Walter Benjamin ile Yahudi mistisizmi ve Kabala üstüne yapıtlarıyla tanınan Gerschom Scholem’in dostluğu, Benjamin’in 1940’ta Fransa-İspanya sınırında intiharıyla sonlanana dek gücünden hiçbir şey kaybetmeden devam etmiştir.

Bugün bildiğimiz eserlerinin ortaya çıkış ve yazılış süreçleri, dönemin entelektüel kişilikleri, edebiyat tartışmaları, Kafka, Baudleaire, Yahudilik, savaş ve ölüm mektupların satırlarında kendisini gösterirken, zor zamanlarda insan olarak var kalabilmenin ne kadar ağır bir yükü taşımak anlamına geldiği de apaçık bir biçimde ortaya çıkıyor. Tüm bu kaygının ve belirsizliğin içinde bile zihinsel üretimlerini hayatta kalma faaliyetlerinin asli öğesi olarak görmeyi sürdüren Benjamin ve Scholem tekerrür etmekte hiç kararsız olmayan tarih için de bir tinsel direniş belgesi sunuyorlar.

“Bugün yayımlanmasını sağladığımız her satır –bu satırları miras bıraktığımız gelecek ne denli belirsiz olursa olsun– bu karanlık dönemin güçlerinin karşısında kazanılmış bir zaferdir.”

Devamını Göster

₺58.00

Satın Al Tüm Ürünler

Hazırlayan: Ögetay Kayalı

Referanslar

1. R. Shankar, Principles of Quantum Mechanics, "Mathematical Introduction"

2. 3Blue1Brown, Essence of Linear Algebra, "Linear combinations, span, and basis vectors", <https://youtu.be/k7RM-ot2NWY?list=PLZHQObOWTQDPD3MizzM2xVFitgF8hE_ab>